您现在的位置是:首页 >技术教程 >数据结构与算法(七)网站首页技术教程
数据结构与算法(七)
简介数据结构与算法(七)
二叉树
如果说树中的每个结点最多只能有两个子结点,这样的树我们就称为二叉树,二叉树可以为空。
特点:
- 每个结点最多有两棵子树,所以二叉树中不存在度大于二的结点棵树中,最大的结点的度称为树的度,结点的度:结点所拥有的了树的个数
- 左子树和右子树是有顺序的,次序不能任意的颠倒
- 即使树某结点只有一棵子树,也要去区分它是左子树还是右子树
性质:
- 在二叉树中,第i层上最多有2^i-1次结点 (i>=1) 第一层: 2 ^1-1
- 在二叉树中,如果深度为k,那么最多有2^k - 1个结点
形态:
- 空树
- 只有一个根结点
- 只有一个左子树
- 只有一个右子树
- 左子树、右子树都有
满二叉树:在一棵二叉树中,所有的分支结点都存在左子树和右子树,并目叶了都在同一层上。
完全二叉树: 除最后一层外,每一层上的结点数均达到最人值。最后一层只缺少有边的若干结点
满二叉树一定是完全二叉树,反过来不一定成立
二叉树的存储:数组、链表,最合适用链表
二叉搜索树
二叉搜索树,BST,binary search tree。二叉查找树、二叉排序树。
二叉搜索树其实就是普通的二叉树上加了一些限制
限制与要求
二叉树对于结点是没有任何的限制,但是在二叉搜索树中在插入子结点的有一些特殊的要求:
- 非空左子树的所有的键值都小于其根结点的键值
- 非空右子树的所有键值都大于其根结点的键值
- 左右子树本身也都是二叉搜索树
二叉搜索树的特点:相对较小的值总是保存在左子结点上,相对较大的值总是保存在右子结点上
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
// 相对小的值:左边 相对大的值:右边
class BinarySearchTree {
constructor() {
// 根节点
this.root = null;
}
// 插入值比较
insertNode(node, newNode) {
if (newNode.value > node.value) {
// 右边
if (node.right === null) {
node.right = newNode
} else {
this.insertNode(node.right, newNode);
}
} else if (newNode.value < node.value) {
// 左边
if (node.left === null) {
node.left = newNode
} else {
this.insertNode(node.left, newNode);
}
}
}
// 插入,判断空树
insert(value){
let newNode = new Node(value);
if(this.root === null){
this.root = newNode;
}else{
this.insert(this.root,newNode)
}
}
}
const bst = new BinarySearchTree();
遍历
遍历:不重复的访问二叉树中所有的结点,
方式:先序遍历,中序遍历,后序遍历
1.先序遍历
- 访问根结点
- 先序遍历其左子树
- 先序遍历其右子树
2.中序遍历
- 先递归遍历其左子树,从最后一个左子树开始存入数组,
- 然后回溯遍历双亲结点,
- 再是右子树。递归循环
3.后序遍历
- 后序遍历其左子树
- 后序遍历其右子树
- 访问根结点
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
// 相对小的值:左边 相对大的值:右边
class BinarySearchTree {
constructor() {
// 根节点
this.root = null;
}
// 先序遍历
preOrederTraversal(cb){
this.preOrderNode(this.root,cb);
}
preOrderNode(node,cb){
// 空节点直接返回
if(node === null) return
// 打印
cb(node.value);
//遍历所有左子树
this.preOrderNode(node.left,cb);
// 遍历所有右子树
this.preOrderNode(node.right,cb);
}
// 中序遍历
inOrederTraversal(cb){
this.inOrderNode(this.root,cb);
}
inOrderNode(node,cb){
// 空节点直接返回
if(node === null) return
//遍历所有左子树
this.inOrderNode(node.left,cb);
// 打印
cb(node.value);
// 遍历所有右子树
this.inOrderNode(node.right,cb);
}
// 后序遍历
afterOrederTraversal(cb){
this.afterOrderNode(this.root,cb);
}
afterOrderNode(node,cb){
// 空节点直接返回
if(node === null) return
//遍历所有左子树
this.afterOrderNode(node.left,cb);
// 遍历所有右子树
this.afterOrderNode(node.right,cb);
// 打印
cb(node.value);
}
}
const bst = new BinarySearchTree();
const rst = []
const cb = (val)=>{
rst.push(val);
}
bst.preOrederTraversal(cb);4.最大值与最小值
max(){
let node = this.root;
while(node.right !== null){
node = node.right;
}
return node.value
}
min(){
let node = this.root;
while(node.left !== null){
node = node.left;
}
return node.value
}5、寻找特定的值
search(val) {
let node = this.root;
while (node !== null) {
if (node.value > val) {
node = node.left;
} else if (node.value < val) {
node = node.right;
}else{
return true;
}
}
}6.删除
三种情况
- 没有子树
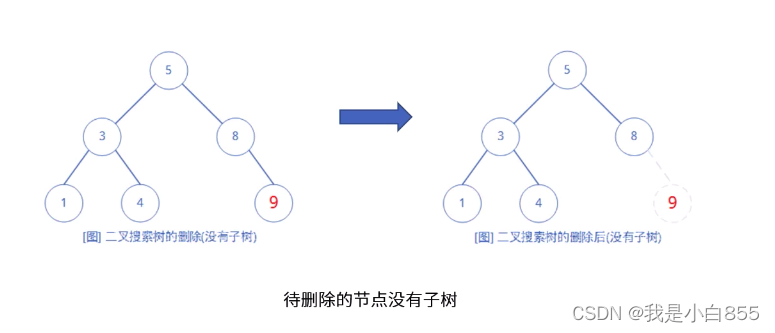
- 仅有一棵子树

- 有两棵子树(保证中序遍历顺序不变)
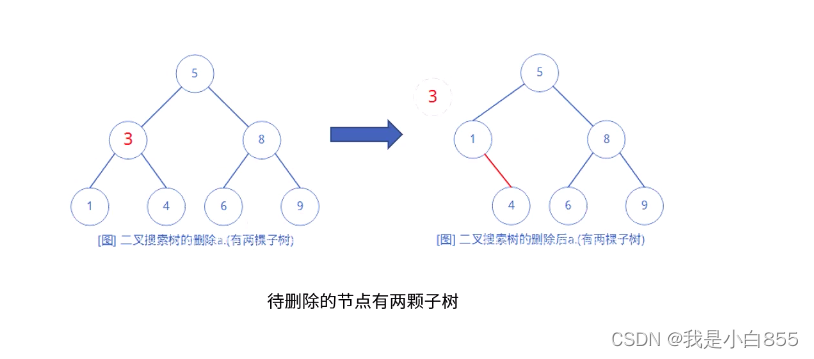
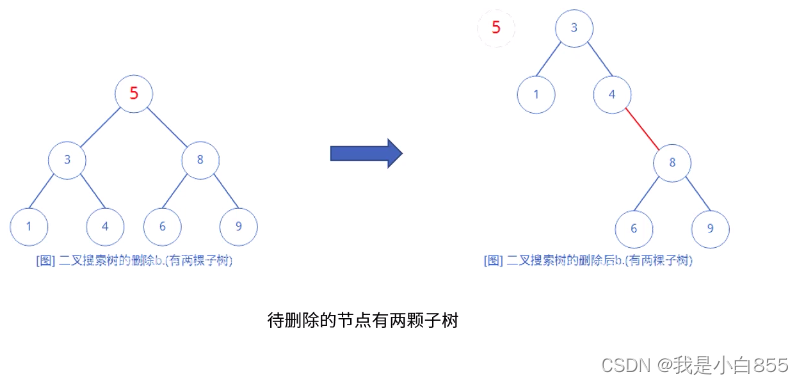
二叉搜索树的优点:作为数据存储的结构有重要的意义,可以快速的找到给定的关键字的数据项,并且可以快速的插入和删除数据
二叉搜索树的缺点:具有局限性。同样的数据,可以对应不同的二叉搜索树
比较好的二叉搜索树的结构:左右分布均匀的,但是我们插入连续的数据的时候,会导致数据分布不均匀 我们就把这个分布不均匀的树称之为非平衡树
平衡树: AVL,红黑树
当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可以降低树的高度,从而减少平均搜索长度。
风语者!平时喜欢研究各种技术,目前在从事后端开发工作,热爱生活、热爱工作。






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结