您现在的位置是:首页 >技术交流 >【数据结构】图的定义,存储,遍历网站首页技术交流
【数据结构】图的定义,存储,遍历
?专栏【数据结构】
?喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。
?音乐分享【Dream It Possible】
大一同学小吉,欢迎并且感谢大家指出我的问题?
目录
?前言
图是一种比线性表和树更为复杂的数据结构。在线性表中,数据元素之间仅有线性关系,每个数据元素只有一个直接前驱和一个直接后继;在树结构中,数据元素之间有着明显的层次关系,并且每一层中的数据元素可能和下一层中的多个元素(其孩子结点)相关,但只能和上一层中一个元素(其双亲结点)相关;而在图结构中,结点之间的关系可以是任意的,图中任意两个数据元素都可能相关。由此,图的应用极为广泛,已渗入诸如物理、化学、通信、计算机,以及数学等领域。在离散数学中,图论是专门研究图的性质的数学分支,而在数据结构中,则应用图论的知识讨论如何在计算机上实现图的操作,因此本章主要介绍图的存储结构,以及若干图的操作的实现。
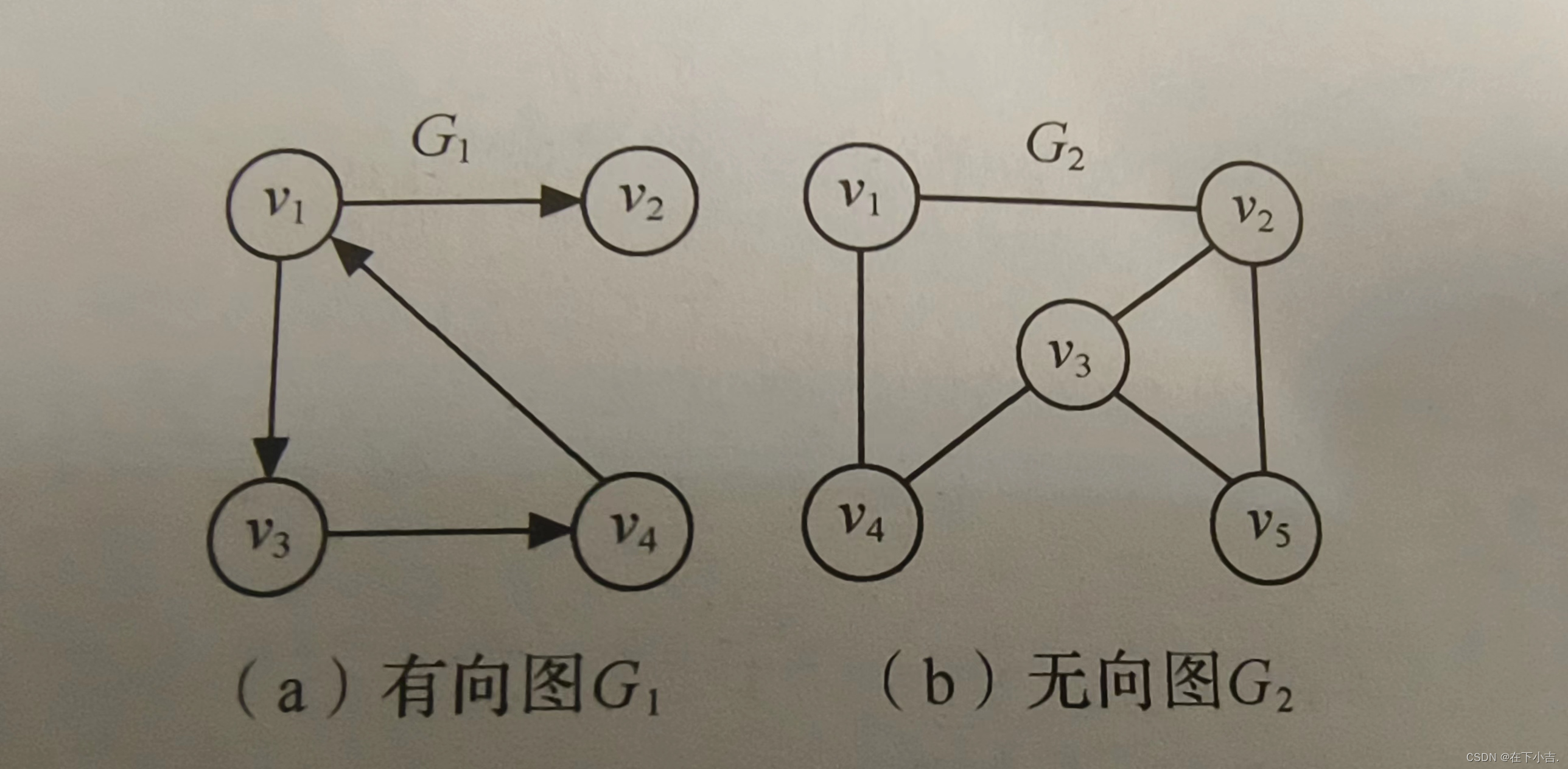
?图的定义
图(Graph)G由两个集合V和E组成,记为G=(V,E),其中V是顶点的有穷非空集合,E是V中顶点偶对的有穷集合,这些顶点偶对称为边。V(G)和E(G)通常分别表示图G的顶点集合和边集合,E(G)可以为空集。若E(G)为空,则图G只有顶点而没有边。
对于图G,若边集E(G)为有向边的集合,则称该图为有向图;若边集E(G)为无向边的集合,则称该图为无向图。
在有向图中,顶点对<x,y>是有序的,它称为从顶点x到顶点y的一条有向边。因此,<x,y>与1是不同的两条边。顶点对用尖括号括起来,对<x,y>而言,x是有向边的始点,y是有向边的终点。<x,y>也称作一条弧,则x为弧尾,y为弧头。
在无向图中,顶点对(x,y)是无序的,它称为与顶点x和顶点y相关联的一条边。这条边没有特定的方向,(x,y)与(y,x)是同一条边。为了有别于有向图,无向图的顶点对用一对圆括号括起来。
?️?有向完全图
有n(n-1)条弧 的图
?️?无向完全图
有n(n-1)/2条边 的图
?存储结构
?️?邻接矩阵
表示顶点之间相邻关系的矩阵,设G(V,E)是具有n个顶点的图,那么G的邻接矩阵有如下性质
(矩阵实在是画不好,绘图能力欠佳,也请大家多多包容?)
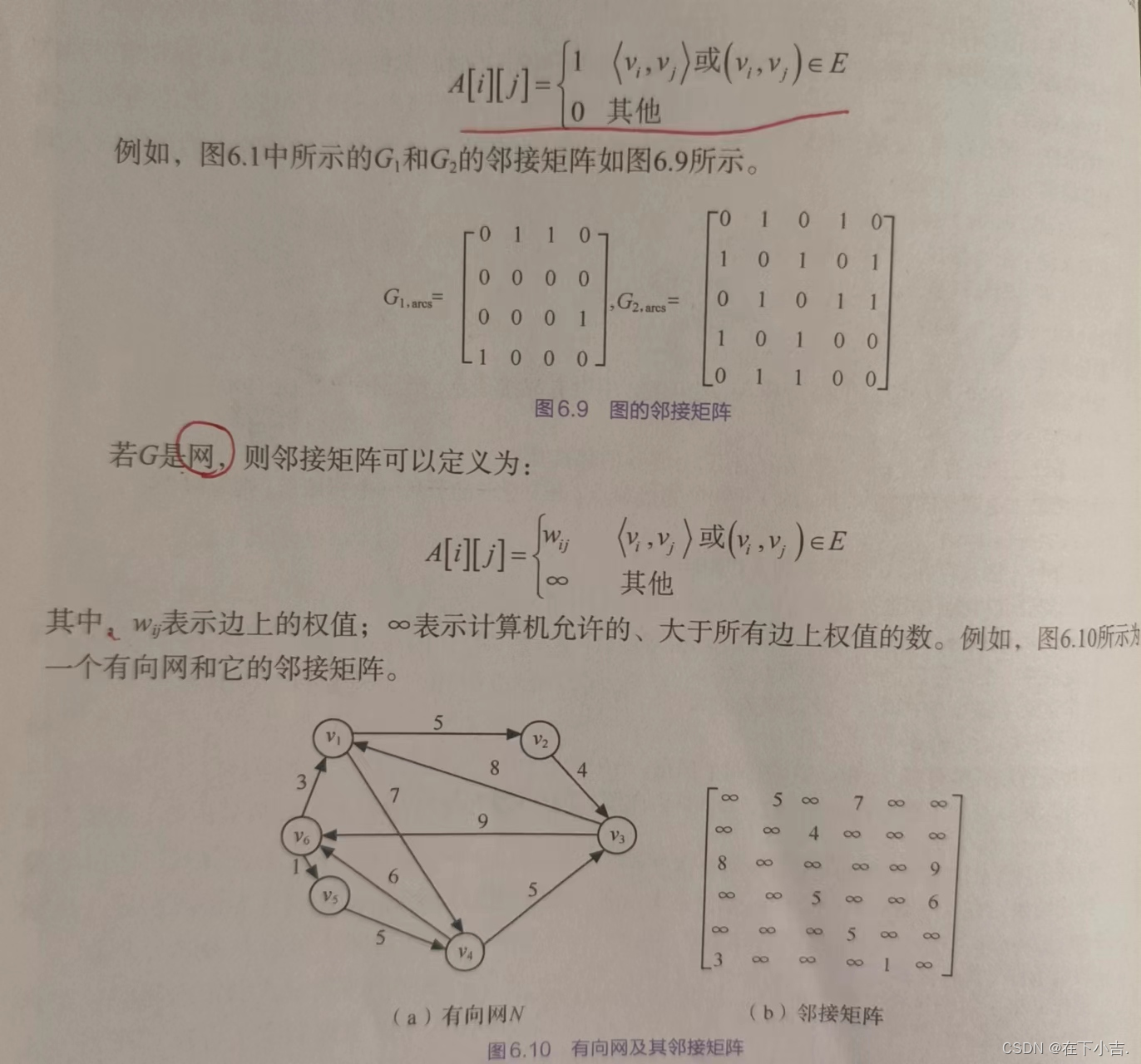
使用邻接矩阵表示图,除了一个用于存储邻接矩阵的二维数组外,还需要一个一维数组来存储顶点信息
?代码
//图的 邻接矩阵 存储表示
#define MaxInt 32767 //表示极大值,即 ∞
#define MVNum 100 //最大顶点数
typedef int VerTexType; //设顶点的数据类型为字符型
typedef int ArcType; //假设边的权值类型为整型
typedef struct{
VerTexType vexs[MVNum]; //顶点表
ArcType arcs[MVNum][MVNum]; //邻接矩阵
int vexnum,arcnum; //图的当前点数和边数
}AMGraph; ?️?采用邻接矩阵表示法创建无向 网
?算法步骤
1.输入总顶点数和总边数
2.依次输入点的信息并将其存入顶点表中
3.初始化邻接矩阵,每个权值初始化为最大值
4.构造邻接矩阵,依次输入每条边依附的顶点以及其权值,确定两个顶点在图中的位置之后,使相应边赋予相应的权值,同时使其对称边赋予相同的权值
?算法描述
int located(AMGraph &G, VerTexType v)
{
for (int i = 0; i < G.vexnum; i++) {
if (G.vexs[i] == v) {
return i;
}
}
return -1; // 未找到,返回 -1
}
int Create(AMGraph &G)
{
cin>>G.vexnum>>G.arcnum;
for(i=0;i<G.vexnum;i++)
{
cin>>G.vexs[i];
}
for(i=0;i<G.vexnum;i++)
{
for(j=0;j<G.vexnum;j++)
{
G.arcs[i][j]=MaxInt;
}
}
for(int k=0;k<G.arcnum;k++)
{
cin>>v1>>v2>>w;
i=located(G,v1);
j=located(G,v2);
G.arcs[i][j]=w;
G.arcs[j][i]=G.arcs[i][j];
}
return 1;
}?️?采用邻接矩阵表示法创建无向 网
进行两处改动即可
1.初始化邻接矩阵时,把边的权值初始化为0
2.构造邻接矩阵时,把权值w修改为1即可
?图的遍历
图的遍历也是从图的某一顶点出发,按照某种方法对图的所有顶点进行访问且访问一次
实质:找每个节点的邻接点
?️?深度优先遍历
?算法步骤
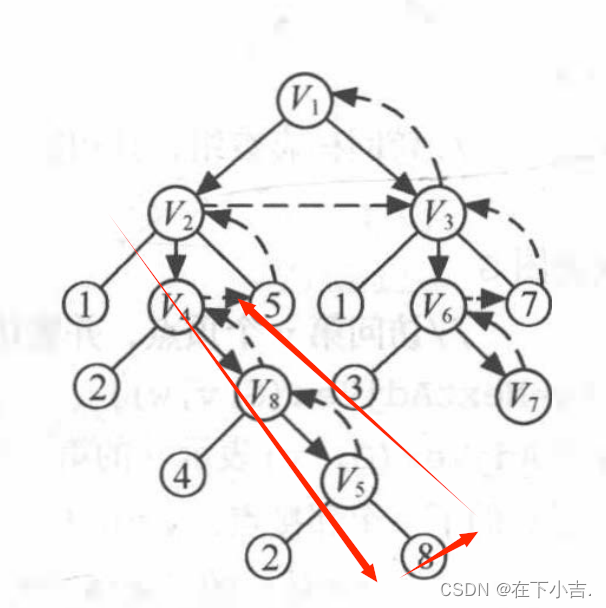
?算法描述
void DFS(AMGraph G, int v)
{
printf("%d ", G.vexs[v]); // 访问顶点 v
visited[v] = true; // 标记为已访问
for (int w = 0; w < G.vexnum; w++)
{
if (G.arcs[v][w] != MaxInt && !visited[w])
{
DFS(G, w); // 对未访问的邻接顶点递归调用DFS
}
}
}?广度优先遍历
?算法步骤
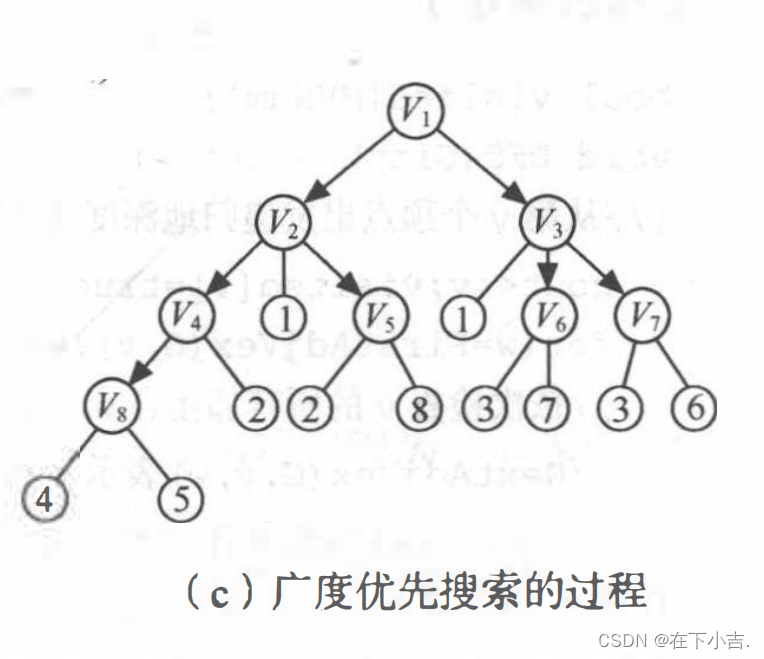
?算法描述
void BFS(AMGraph G, int v)
{
int front = 0, rear = 0;
int queue[MVNum]; // 定义队列
printf("%d ", G.vexs[v]);
visited[v] = true;
queue[rear++] = v; // 将顶点 v 入队
while (front != rear)
{
int k = queue[front++]; // 出队一个顶点 k
for (int w = 0; w < G.vexnum; w++)
{
if (G.arcs[k][w] != MaxInt && !visited[w])
{
printf("%d ", G.vexs[w]); // 访问顶点 w
visited[w] = true;
queue[rear++] = w; // 将顶点 w 入队
}
}
}
}?附加
?️?实验题目
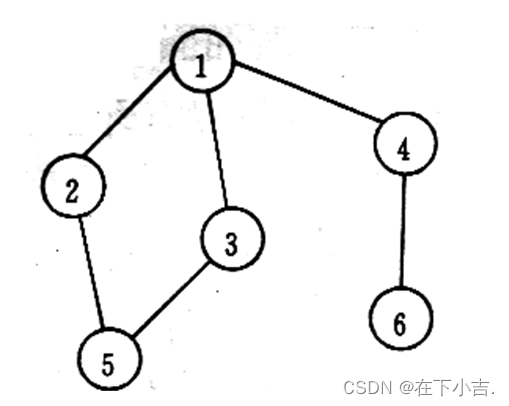
1.使用邻接矩阵的方式存储上边无向图;
2.以矩阵的形式输出无向图
3.在邻接矩阵的基础上实现深度优先遍历和广度优先遍历。
?️?代码
/*
6 6
1 2 3 4 5 6
1 2 1
2 5 1
5 3 1
3 1 1
1 4 1
4 6 1
*/
#include<iostream>
using namespace std;
#define MaxInt 32767 //表示极大值,即 ∞
#define MVNum 100 //最大顶点数
typedef int VerTexType; //设顶点的数据类型为字符型
typedef int ArcType; //假设边的权值类型为整型
typedef struct{
VerTexType vexs[MVNum]; //顶点表
ArcType arcs[MVNum][MVNum]; //邻接矩阵
int vexnum,arcnum; //图的当前点数和边数
}AMGraph; //Adjacency Matrix Graph
int v1,v2,i,j,k,w;
int located(AMGraph &G, VerTexType v)
{
for (int i = 0; i < G.vexnum; i++) {
if (G.vexs[i] == v) {
return i;
}
}
return -1; // 未找到,返回 -1
}
int Create(AMGraph &G)
{
cin>>G.vexnum>>G.arcnum;
for(i=0;i<G.vexnum;i++)
{
cin>>G.vexs[i];
}
for(i=0;i<G.vexnum;i++)
{
for(j=0;j<G.vexnum;j++)
{
G.arcs[i][j]=MaxInt;
}
}
for(int k=0;k<G.arcnum;k++)
{
cin>>v1>>v2>>w;
i=located(G,v1);
j=located(G,v2);
G.arcs[i][j]=w;
G.arcs[j][i]=G.arcs[i][j];
}
return 1;
}
bool visited[MVNum];
// 深度优先遍历
void DFS(AMGraph G, int v)
{
printf("%d ", G.vexs[v]); // 访问顶点 v
visited[v] = true; // 标记为已访问
for (int w = 0; w < G.vexnum; w++)
{
if (G.arcs[v][w] != MaxInt && !visited[w])
{
DFS(G, w); // 对未访问的邻接顶点递归调用DFS
}
}
}
// 广度优先遍历
void BFS(AMGraph G, int v)
{
int front = 0, rear = 0;
int queue[MVNum]; // 定义队列
printf("%d ", G.vexs[v]);
visited[v] = true;
queue[rear++] = v; // 将顶点 v 入队
while (front != rear)
{
int k = queue[front++]; // 出队一个顶点 k
for (int w = 0; w < G.vexnum; w++)
{
if (G.arcs[k][w] != MaxInt && !visited[w])
{
printf("%d ", G.vexs[w]); // 访问顶点 w
visited[w] = true;
queue[rear++] = w; // 将顶点 w 入队
}
}
}
}
int main()
{
AMGraph G;
Create(G);
printf("存储成功
");
// 输出邻接矩阵
for (int i = 0; i < G.vexnum; i++)
{
for (int j = 0; j < G.vexnum; j++)
{
if (G.arcs[i][j] == MaxInt)
{
printf("∞ ");
}
else
{
printf("%d ", G.arcs[i][j]);
}
}
printf("
");
}
// 初始化访问标记数组
for (int i = 0; i < G.vexnum; i++)
{
visited[i] = false;
}
printf("深度优先遍历: ");
for (int i = 0; i < G.vexnum; i++)
{
if (!visited[i])
{
DFS(G, i);
}
}
printf("
");
// 重置访问标记数组
for (int i = 0; i < G.vexnum; i++)
{
visited[i] = false;
}
printf("广度优先遍历: ");
for (int i = 0; i < G.vexnum; i++)
{
if (!visited[i])
{
BFS(G, i);
}
}
printf("
");
return 0;
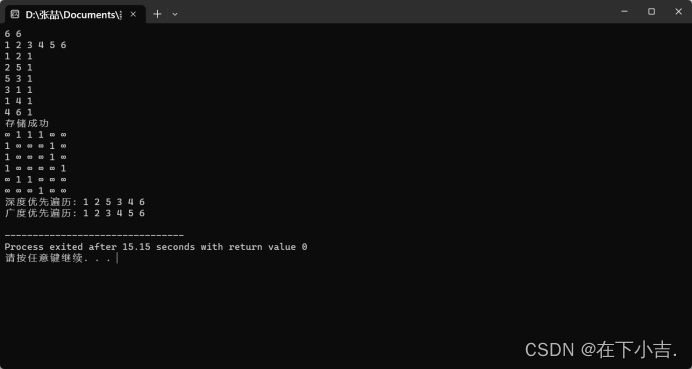
}?️?运行结果
?如果大家有不明白的地方,或者文章有问题,欢迎大家在评论区讨论,指正?






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结