您现在的位置是：首页 >其他 >【4.17】贪心算法入门网站首页其他

什么是贪心？

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。

刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心。

贪心的解题步骤？

贪心算法一般分为如下四步：

• 将问题分解为若干个子问题
• 找出适合的贪心策略
• 求解每一个子问题的最优解
• 将局部最优解堆叠成全局最优解

这个四步其实过于理论化了，我们平时在做贪心类的题目 很难去按照这四步去思考，真是有点“鸡肋”。

做题的时候，只要想清楚 局部最优 是什么，如何推导出全局最优，其实就够了。

总之，说白了就是常识性推导加上举反例。

LeetCode

• 455. 分发饼干 - 力扣（LeetCode）

  局部最优是大饼干分给胃口大的小朋友，并且推不出反例，还能推导出全局最优。

  class Solution {
      public int findContentChildren(int[] g, int[] s) {
          Arrays.sort(g);
          Arrays.sort(s);
          int count = 0;
          //表示当前使用的
          //局部最优：大饼干给胃口大的
          //全局最优，可以满足最多的孩子。
          int index = s.length - 1;
          for(int i = g.length - 1 ; i >= 0 ; i --){
              if(index >= 0 && s[index] >= g[i]){
                  count ++;
                  index --;
              }
          }
          return count;
      }
  }
  

• 376. 摆动序列 - 力扣（LeetCode）

  思路一：贪心算法

  局部最优：删除单调坡度上的节点，那么这个坡度可以有两个局部峰值。

  

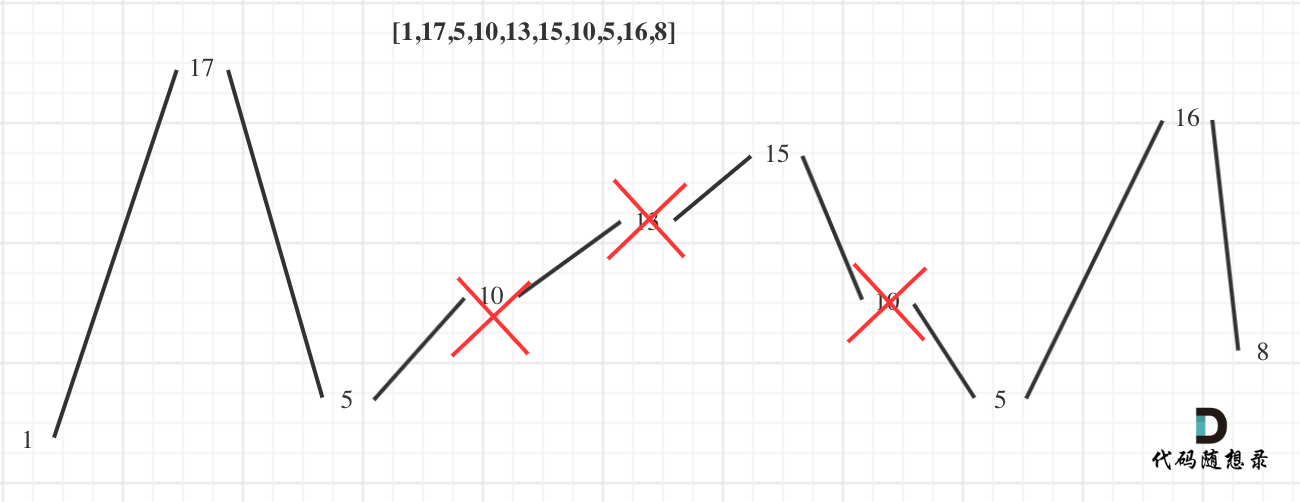
  整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。

  实际操作上，其实连删除的操作都不用做，因为题目要求的是最长摆动子序列的长度，所以只需要统计数组的峰值数量就可以了（相当于是删除单一坡度上的节点，然后统计长度）

  这就是贪心所贪的地方，让峰值尽可能的保持峰值，然后删除单一坡度上的节点

  该题一共有三种情况：

  1. 上下坡中有平坡

  2. 数组首尾两端

  3. 单调坡中有平坡

  class Solution {
      int len = 0;
      int ans = 0;
      public int wiggleMaxLength(int[] nums) {
          if(nums.length <= 1) return nums.length;
          int index = 0;
          int curDiff = 0; //当前一对差值
          int preDiff = 0; //前一对差值
          int result = 1; //记录峰值个数，序列默认最右边有一个峰值。
          for(int i = 0 ; i < nums.length - 1 ; i ++){
              curDiff = nums[i + 1] - nums[i];
              //如果出现峰值，就统计结果。
              //为什么允许preDiff = 0 ？ 为了应对上下坡中有平坡的这种情况。
              //为什么result初始为 1？ 为了统计数组最左面和最右面的值。
              //为什么找到峰值才更新preDiff？ 为了应对单调坡度有平坡的情况。preDiff不能实时更新。
              if((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)){
                  result ++;
                  preDiff = curDiff;
              }
          }
          return result;
      }
  }
  

• 53. 最大子数组和 - 力扣（LeetCode）

  解法一：动态规划

  class Solution {
      public int maxSubArray(int[] nums) {
          //dp[i]：nums中下标i之前（包括i）的最大连续子数组之和为dp[i]。
          int n = nums.length;
          int [] dp = new int [n];
          dp[0] = nums[0];
          int ans = nums[0];
          for(int i = 1 ; i < nums.length ; i++){
              dp[i] = Math.max(nums[i] , dp[i - 1] + nums[i]);
              ans = Math.max(ans , dp[i]);
          }
          return ans;
      }
  }
  

  解法二：贪心算法，局部最优：碰到为负数的连续和，就将连续和置为0。

  最终会得到全局最优：找到最大的子数组和。

  class Solution {
      public int maxSubArray(int[] nums) {
          int count = 0;
          int result = Integer.MIN_VALUE; 
          for(int i = 0 ; i < nums.length ; i ++){
              count += nums[i];
              if(count > result){
                  result = count;
              }
              if(count <= 0){
                  count = 0;
              }
          }
          return result;
      }
  }
  

  解法三：暴力解法（超时）

  class Solution {
      public int maxSubArray(int[] nums) {
          int count = 0;
          int result = Integer.MIN_VALUE; 
          for(int i = 0 ; i < nums.length ; i ++){
              for(int j = i ; j < nums.length ; j ++){
                  count += nums[j];
                  result = count > result ? count : result;
              }
              count = 0;
          }
          return result;
      }
  }