迷宫问题简介

🚀学习过算法程序设计的应该都学习过迷宫这个问题，迷宫问题主要设计的算法就是DFS-深度优先遍历和BFS-广度优先遍历。
🚀在一个二维数组中，元素为1的位置表示这个位置是墙，0表示有通路，迷宫的入口和出口都是0（否则不会有路径能出去），并且路径不唯一。例如下图：

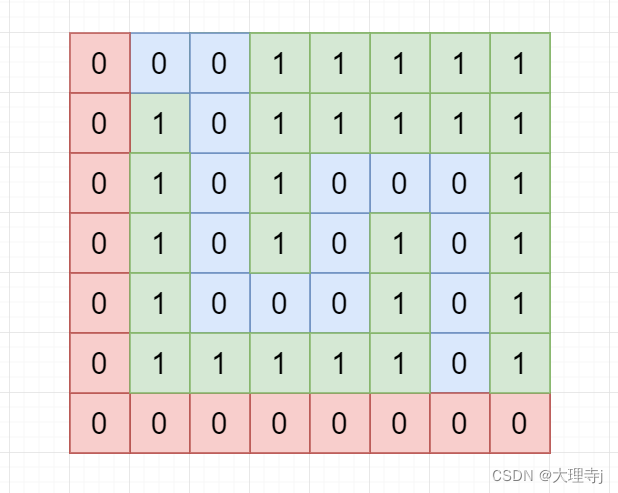
🚀图中这个迷宫有两条路径，分别用粉色和蓝色标记了出来，明显粉色路径的长度是比蓝色路径要短的。

BFS解决迷宫最短路径问题

🚀BFS可以解决最短路径的原因是，BFS是像水波一样逐渐向外圈波及的，很明显最先波及到的通路就是最短路径。

🚀使用BFS算法的思想

一般的广度优先遍历都是采用队列完成的，每次取对头然后将其周围四个位置压到队列当中，然后pop掉对头，这样循环下去直到队列为空就停止。但是这种算法无法记录迷宫走过的路径，所以我才用vector来模拟队列来使用，就相当于对头的数据不pop掉，而是用一个下标来控制，现在走到哪个下标了，并且存储当前位置的结构体中多设置了一个变量prev，存储的是这个位置的上个位置在vector中的下标。这样在迷宫中走到终点的时候，返回这个vector，里面就有我们过的路径了。

🚀代码实现

struct path
{
	int _x;
	int _y;
	int _prev; // 在模拟对列中的下标位置
	path(int x,int y,int prev)
		:_x(x)
		,_y(y)
		,_prev(prev)
	{}
};
bool check(int i, int j, int map[][8], int row, int col)
{
	if (i < 0 || j < 0 || i > row - 1 || j > col - 1)
		return false;
	if (map[i][j] == -1) //走过的位置被设置为-1
		return false;
	if (map[i][j] == 1)
		return false;
	return true;
}

vector<path> BFS(int map[][8], int row, int col)
{
	vector<path> v;
	v.push_back(path(0, 0, -1));
	size_t index = 0;
	int fx[4] = { 0,1,-1,0 };
	int fy[4] = { 1,0,0,-1 };
	int i = 0, j = 0;//当前位置的横纵坐标
	while (index < v.size())
	{
		i = v[index]._x;
		j = v[index]._y;
		for (int k = 0; k < 4; k++)
		{
			int new_i = i + fx[k];
			int new_j = j + fy[k];
			if (check(new_i, new_j, map, row, col))
			{
				v.push_back(path(new_i, new_j, index));
				map[new_i][new_j] = -1;
				if (new_i == row - 1 && new_j == col - 1)
					return v;
			}
		}
		index++;
	}
	cout << "error" << endl;
	return v;
}
int main()
{
	int map[7][8] = {
		{0,0,0,1,1,1,1,1},
		{0,1,0,1,1,1,1,1},
		{0,1,0,1,0,0,0,1},
		{0,1,0,1,0,1,0,1},
		{0,1,0,0,0,1,0,1},
		{0,1,1,1,1,1,0,1},
		{0,0,0,0,0,0,0,0}
	};
	vector<path> res = BFS(map, 7, 8);
	int i = res.size() - 1;
	while (i >= 0)
	{
		cout << "(" << res[i]._x << "," << res[i]._y << ")" << endl;
		i = res[i]._prev;
	}
}

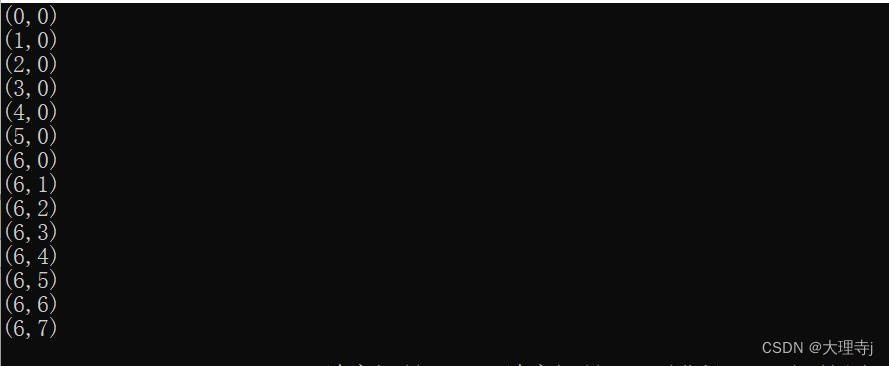
🚀运行结果

🚀你会发现打印的结果是从终点走向起点的，我们可以对其做一下修改。使用递归的方式逆向打印出结果。

void Print(vector<path>& v, int index)
{
	if (index == 0)
	{
		cout << "(" << v[index]._x << "," << v[index]._y << ")" << endl;
		return;
	}
	Print(v, v[index]._prev);
	cout << "(" << v[index]._x << "," << v[index]._y << ")" << endl;
}

🚀这样我们就能得到正向的路径了。

DFS记录迷宫路径

🚀BFS算法思想

深度优先搜索是，一条道走到黑，走不通再换另一条路，对于深度优先搜索，我们可以用栈来记录它的路径，每次进入程序后，先将当前位置压栈，再让他向上下左右去试探，值得注意的是要在最后进行弹栈处理，因为如果上下左右都我没有返回true表明从此位置出发是到不了终点的，说明此位置不在最终的路径当中，所以要弹栈。并且在开始的时候将此位置压栈后，要将此位置对应的数据改为-1，表明在后面的递归中不能往回走了（会造成死循环），并且在弹栈后要将此位置的值修改为0，这是因为这层函数栈帧已经结束，返回到上一层栈帧中，而返回到上一层栈帧的时候，这个位置是没有被访问的。

🚀代码实现

bool DFS(int map[][8], int row, int col, stack<_path>& st,int i,int j)
{
	st.push(_path(i, j));
	map[i][j] = -1;
	if (i == row - 1 && j == col - 1)
		return true;
	if (check(i + 1, j, map, row, col))
		if (DFS(map, row, col, st, i + 1, j))
			return true;
	if (check(i, j + 1, map, row, col)) 
		if (DFS(map, row, col, st, i, j + 1))
			return true;
	if (check(i - 1, j, map, row, col))
		if (DFS(map, row, col, st, i - 1, j))
			return true;
	if (check(i, j - 1, map, row, col))
		if (DFS(map, row, col, st, i, j - 1))
			return true;
	map[i][j] = 0;
	st.pop();
	return false;
}

int main()
{
	int map[7][8] = {
		{0,0,0,1,1,1,1,1},
		{0,1,0,1,1,1,1,1},
		{0,1,0,1,0,0,0,1},
		{0,1,0,1,0,1,0,1},
		{0,1,0,0,0,1,0,1},
		{0,1,1,1,1,1,0,1},
		{0,0,0,0,0,0,0,0}
	};
	//vector<path> res = BFS(map, 7, 8);
	//int i = res.size() - 1;
	/*while (i >= 0)
	{
		cout << "(" << res[i]._x << "," << res[i]._y << ")" << endl;
		i = res[i]._prev;
	}*/
	//Print(res, i);
	stack<_path> st;
	DFS(map, 7, 8, st, 0, 0);
	while (!st.empty())
	{
		cout << "(" << st.top()._x << "," << st.top()._y << ")" << endl;
		st.pop();
	}
}

🚀运行结果

可以返现这个路径仍然是从终点到起点的，所以如果想要正序输出那么仍然要做修正。
但是还要注意的是，迷宫中有两条路径，栈中只记录了一条路径，恰巧这个路径是最短路径，注意这是恰巧，这和你第一步的走向有关。如果你改变走向结果也可能会变，所以DFS并不适合求最短路径，但是用来求路径还是没毛病的。

bool DFS(int map[][8], int row, int col, stack<_path>& st,int i,int j)
{
	st.push(_path(i, j));
	map[i][j] = -1;
	if (i == row - 1 && j == col - 1)
		return true;
	if (check(i, j + 1, map, row, col)) //先向右走
		if (DFS(map, row, col, st, i, j + 1))
			return true;
	if (check(i + 1, j, map, row, col))
		if (DFS(map, row, col, st, i + 1, j))
			return true;
	if (check(i - 1, j, map, row, col))
		if (DFS(map, row, col, st, i - 1, j))
			return true;
	if (check(i, j - 1, map, row, col))
		if (DFS(map, row, col, st, i, j - 1))
			return true;
	map[i][j] = 0;
	st.pop();
	return false;
}

🚀可以看到先向右走的时候，栈中存储的数据就是另一条路径了，这也验证了DFS不适合求最短路径。注意我说的是不适合不代表DFS不能求最短路径。

DFS解决迷宫所有路径问题

🚀思路

求所有路径，我们可以使用vector，每一步都记录在vector中，如果当前位置到达了终点，那么就打印vector中的路径。

🚀代码

void DFS2(int map[][8], int row, int col, int i, int j, vector<_path> v)
{
	v.push_back(_path(i, j));
	map[i][j] = -1;
	if (i == row - 1 && j == col - 1)
	{
		for (int i = 0; i < v.size(); i++)
		{
			cout << "(" << v[i]._x << "," << v[i]._y << ")" << endl;
		}
		cout << "-------------------------------" << endl;
	}
	if (check(i, j + 1, map, row, col)) //先向右走
		DFS2(map, row, col, i, j + 1,v);
	if (check(i + 1, j, map, row, col))
		DFS2(map, row, col,  i + 1, j, v);
	if (check(i - 1, j, map, row, col))
		DFS2(map, row, col,  i - 1, j,v);
	if (check(i, j - 1, map, row, col))
		DFS2(map, row, col,  i, j - 1,v);
	map[i][j] = 0;
}

🚀结果展示