【数据结构】算法的时间复杂度和空间复杂度（下）（附leetcode练习题）网站首页 技术杂谈

【数据结构】算法的时间复杂度和空间复杂度（下）（附leetcode练习题）

fighting小泽 2023-05-19 00:00:03

简介【数据结构】算法的时间复杂度和空间复杂度（下）（附leetcode练习题）

☃️个人主页：fighting小泽
🌸作者简介：目前正在学习C语言和数据结构
🌼博客专栏：数据结构
🏵️欢迎关注：评论👊🏻点赞👍🏻留言💪🏻

1. 空间复杂度

空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用的额外的存储空间大小的量度。
空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似，也使用大O渐进表示法。
注意：函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。

1.1 空间复杂度的例子

实例1：

计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n)
{
  assert(a);
   for (size_t end = n; end > 0; --end)
  {
    int exchange = 0;
    for (size_t i = 1; i < end; ++i)
    {
       if (a[i-1] > a[i])
     {
       Swap(&a[i-1], &a[i]);
       exchange = 1;
     }
    }
    if (exchange == 0)
    break;
 }
}

有的朋友会觉得这个冒泡排序的空间复杂度是 O(N),有的会觉得空间复杂度是 O(1)。为什么会觉得是O(N)呢，因为这里有一个数组，这个数组有N个空间。但是数组的N个空间算不算是冒泡排序的消耗？

其实是不算的，因为这个数组存储N个数据，我们对它进行排序其实是对数组的内容进行处理，它本身就要有，不是因为我们要排序而自己开的空间，在冒泡排序里面创建的end和exchange是常数个，所以它的空间复杂度是O(1).

实例2:

// 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
 if(n==0)
 return NULL;
 
 long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
 fibArray[0] = 0;
 fibArray[1] = 1;
 for (int i = 2; i <= n ; ++i)
 {
 fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
 }
 return fibArray;
}

正常的斐波那契数列是三个变量来回倒，它的空间复杂度就是O(1),但是我们这里是malloc了一个数组，这个数组有N+1个空间，所以它的空间复杂度就是经典的O(N)。

实例3：

 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{
 if(N == 0)
 return 1;
 
 return Fac(N-1)*N;
}

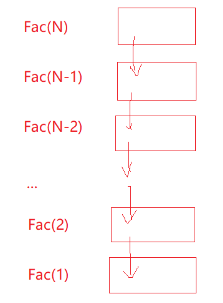
这个时候就涉及到一个栈帧的问题了，每次函数调用会建立一个函数栈帧，相当于建立了N个栈帧，那每个栈帧开辟多少空间呢？
每个栈帧里面其实只有常数个，但是因为创建了N个栈帧，所以它的空间复杂度是O(N)。

在这里插入图片描述
实例4：

计算斐波那契递归Fib的空间复杂度？
long long Fib(size_t N)
{
 if(N < 3)
 return 1;
 
 return Fib(N-1) + Fib(N-2);
}

它的时间复杂度是2 ^ N,可能大多数老铁觉得它的空间复杂度也是
2 ^ N，是一样的。

实际上它不是，它的空间复杂度是不好算的，它的空间复杂度是O(N)。
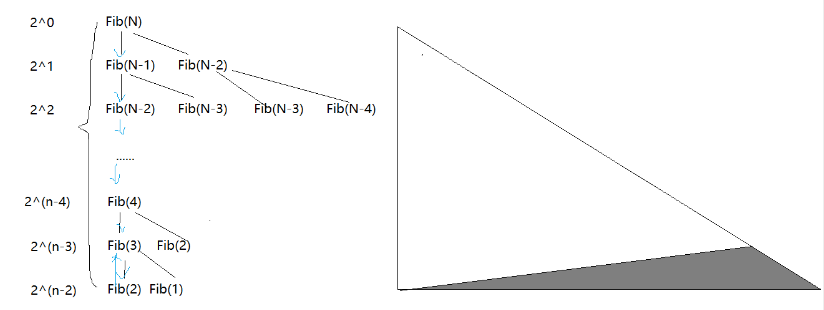
为什么呢？这时候大家就要看到一个问题，递归调用是咋调的？

斐波那契第N项是不是要调用(N-1)和(N-2)啊，那我问大家它是同时调用(N-1)和(N-2)项吗？不是，它会先调用（N-1),然后调用（N-1)下面的(N-2)，然后调用下面的(N-3)，会一直往下调用，调用到第2项之后才回来，再调用右边再回去，再调用右边再回去。那就意味着这个栈帧的建立是这样的，最多会建立多少个栈帧呢？是0到N-2个栈帧，就是N-1个栈帧。他会先往深不断不断去走，走了回来的时候栈帧就销毁了，再调用右边的会跟左边的重复用一个栈帧空间，那最多会建立多少层呢？N层。可以认为最多就建立左边的这一列，再调用右边的会跟左边的重复用一个栈帧空间。

这里有一句话送给大家：时间是一去不复返的，空间是可以重复利用的。时间是累计计算的，空间不累计计算。

在这里插入图片描述
这里我们再看一个代码：

void Func1()
{
	int a = 0;
	printf("%p
", &a);
}
void Func2()
{
	int b = 0;
	printf("%p
", &b);
}
int main()
{
	Func1();
	Func2();

	return 0;
}

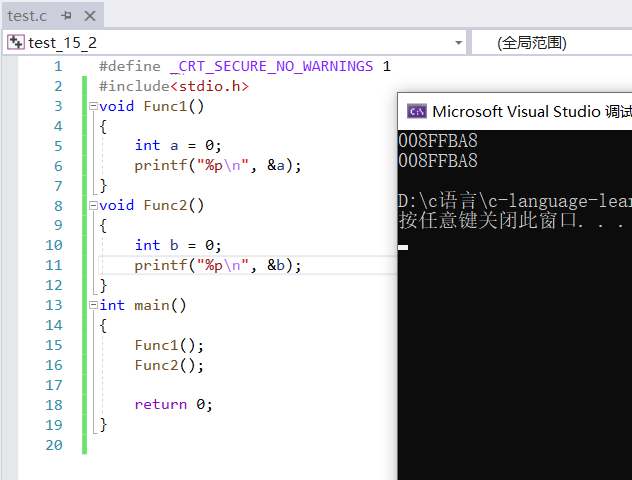
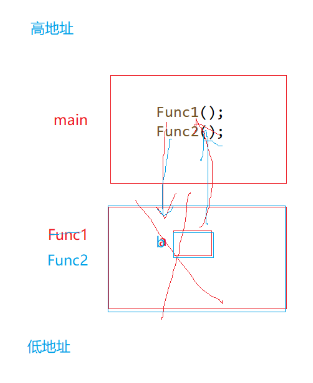
在这里插入图片描述
我们发现，a和b是使用同一块空间的，这时因为函数调用时创立栈帧，函数结束时栈帧也会销毁，但是销毁的这块栈帧空间不是不能使用了，而是归还操作系统了，下一次函数栈帧空间也在这里创建，所以a和b的地址是一样的。同理，刚刚斐波那契数列销毁的空间也会被下一次函数调用所利用。
在这里插入图片描述

2.常见复杂度对比

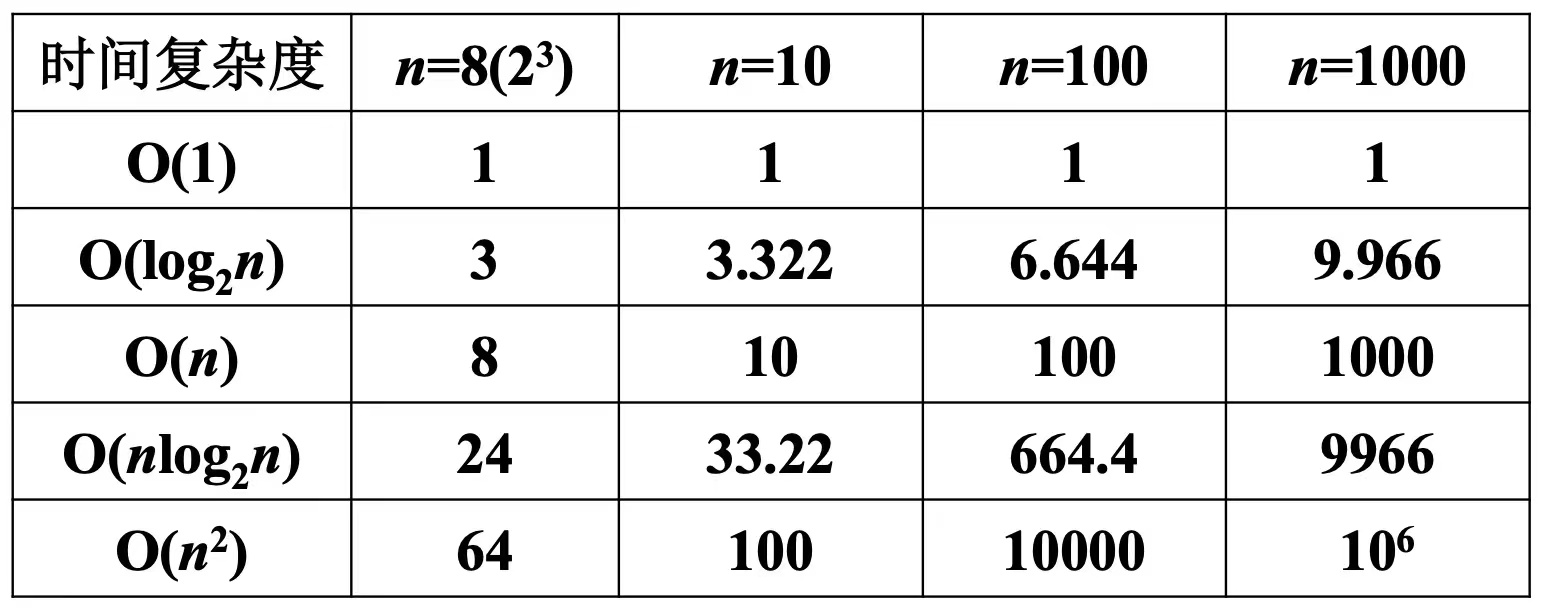
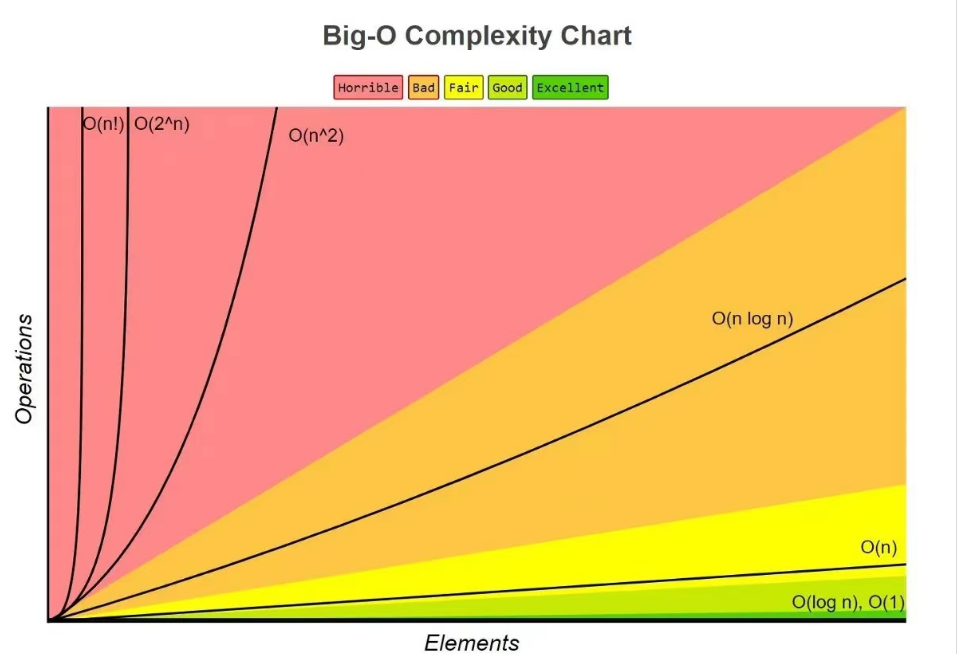
在这里插入图片描述

3.leetcode练习题

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。189 . leetcode - 旋转数组
在这里插入图片描述

1. 暴力求解，旋转K次

我们可以用一个 tmp 记录下最后一个元素，然后进行for循环，把每个元素向右移动一位，再把 tmp 传给第一个元素就行了。大家可以自己试一试，不够这样写在力扣过不去，会超时。

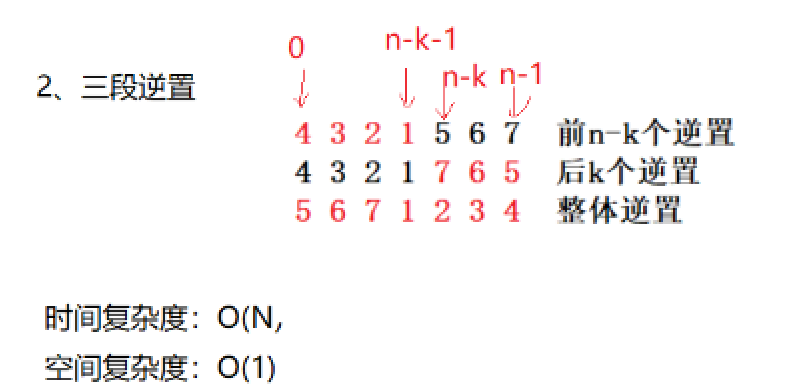
2. 三段逆置

这是个聪明人才能想出来的方法，先把前 N-K 个元素逆置，再把后 K 个逆置，再把整体逆置就完成了
在这里插入图片描述

void swap(int* a, int* b) {
    int t = *a;
    *a = *b, *b = t;
}

void reverse(int* nums, int start, int end) {
    while (start < end) {
        swap(&nums[start], &nums[end]);
        start += 1;
        end -= 1;
    }
}

void rotate(int* nums, int numsSize, int k) {
    k %= numsSize;
    reverse(nums, 0, numsSize - 1);
    reverse(nums, 0, k - 1);
    reverse(nums, k, numsSize - 1);
}

3. 空间换时间

我们可以创建一个新数组，把前 N-K 个元素放到后面，把后 K 个元素放到前面

注意：当 K 大于numsSize的时候相当于把数组转过了一遍，但是直接写 K 会越界，访问到后面的元素，所以我们可以令 k = (i+k)%numsSize

void rotate(int* nums, int numsSize, int k) {
    int newArr[numsSize];
        for (int i = 0; i < numsSize; i++)
    {
        newArr[(i+k)%numsSize] = nums[i];
    }
    for (int i = 0; i <numsSize; i++)
    {
        nums[i]=newArr[i];
    }
}