您现在的位置是：首页 >技术交流 >使用 C 语言验证非均匀概率的离散事件在样本数量足够大时，符合正态分布曲线（通过生成一个PPM格式的图像）网站首页技术交流
使用 C 语言验证非均匀概率的离散事件在样本数量足够大时，符合正态分布曲线（通过生成一个PPM格式的图像）
简介使用 C 语言验证非均匀概率的离散事件在样本数量足够大时，符合正态分布曲线（通过生成一个PPM格式的图像）
我想写本文的原因是看到著名数学科普账号 3Blue1Brown 发布的【官方双语】但是什么是中心极限定理？中提到：不论这个离散型事件的各种情况概率是不是平均的，当数量一定大时，还是会符合正态分布曲线。我就想自己试试看是不是这种情况，因为我觉得中心极限定理和正态分布是一个概率论中很神奇的一部分。
本文使用骰子点数当作离散型事件，求点数之和的概率。先实现均匀分布的状态下的程序，再调整为不均匀分布的概率，完整源代码放在最后，防止因为头文件等问题导致错误。
均匀分布下，点数之和的概率
首先，新建一个数组来存放骰子的点数，如下：
int a[] = {1,2,3,4,5,6};
生成图像使用下面的函数writePPMImage：
void writePPMImage(int* data, int width, int height, const char *filename, int maxIterations)
{
FILE *fp = fopen(filename, "wb");
// write ppm header
fprintf(fp, "P6
");
fprintf(fp, "%d %d
", width, height);
fprintf(fp, "255
");
for (int i = 0; i < width*height; ++i) {
float mapped = pow( std::min(static_cast<float>(maxIterations), static_cast<float>(data[i])) / 256.f, .5f);
unsigned char result = static_cast<unsigned char>(255.f * mapped);
for (int j = 0; j < 3; ++j)
fputc(result, fp);
}
fclose(fp);
printf("Wrote image file %s
", filename);
}
这个函数的参数：
data是一个数组，其中每个元素对应位图的每个像素颜色信息（Z 字排列），也就是说，一个元素（或者说就是像素）对应点数之和中，有一次这个值。width和height是生成位图的尺寸。filename是生成的位图文件。maxIterations是颜色最大值，也就是白色对应的值，这里我们将其设置为256，因为代码中是当作 8 通道色彩。我们只需要黑白，所以也可以更简洁，直接写成1，然后只用0和1两个整数值表示黑白即可。
下面直接写出代码，每一步的介绍请看注释：
int main() {
//设置图片尺寸为1450x1000
int width = 1450;
int height = 1000;
//待会需要随机从中选择一个元素，当作骰子的点数
int a[] = {1,2,3,4,5,6};
//用来存放各种点数之和的数量多数组，这里不要声明空数组，因为一些编译器会给没有值的元素分配一些很奇怪的值，导致运行错误（不像C语言是默认为0）
int* sumArr = new int[width];
//用来存放最后输出图像的像素色彩信息的数组
int* output = new int[width*height];
//样本量为30x1000=30000，也就是取3万次点数之和
for (int i=0; i<height*30; i++) {
//获取到一个随机点数。模6表示随机值范围是0～5，刚好对应前面数组a的每个元素
int temp = a[random()%6];
//下面的循环将会累加100次，也就是表示多少个骰子点数之和
for (int j=0; j<100; j++) {
temp = temp + a[random()%6];
}
//给这个值对应的sumArr的元素加1
sumArr[temp] = sumArr[temp]+1;
}
//因为输出图像的时候，条状图是从底部开始的，所以写这样的一个转换
for (int i=0; i<width; i++) {
for (int j=height-1; j>=height-sumArr[i]; j--) {
output[j*width+i]=256;
}
}
//输出图像
writePPMImage(output, width, height, "output.ppm", 256);
delete[] sumArr;
delete[] output;
return 0;
}
生成的 3 万个样本对应的图像如下：
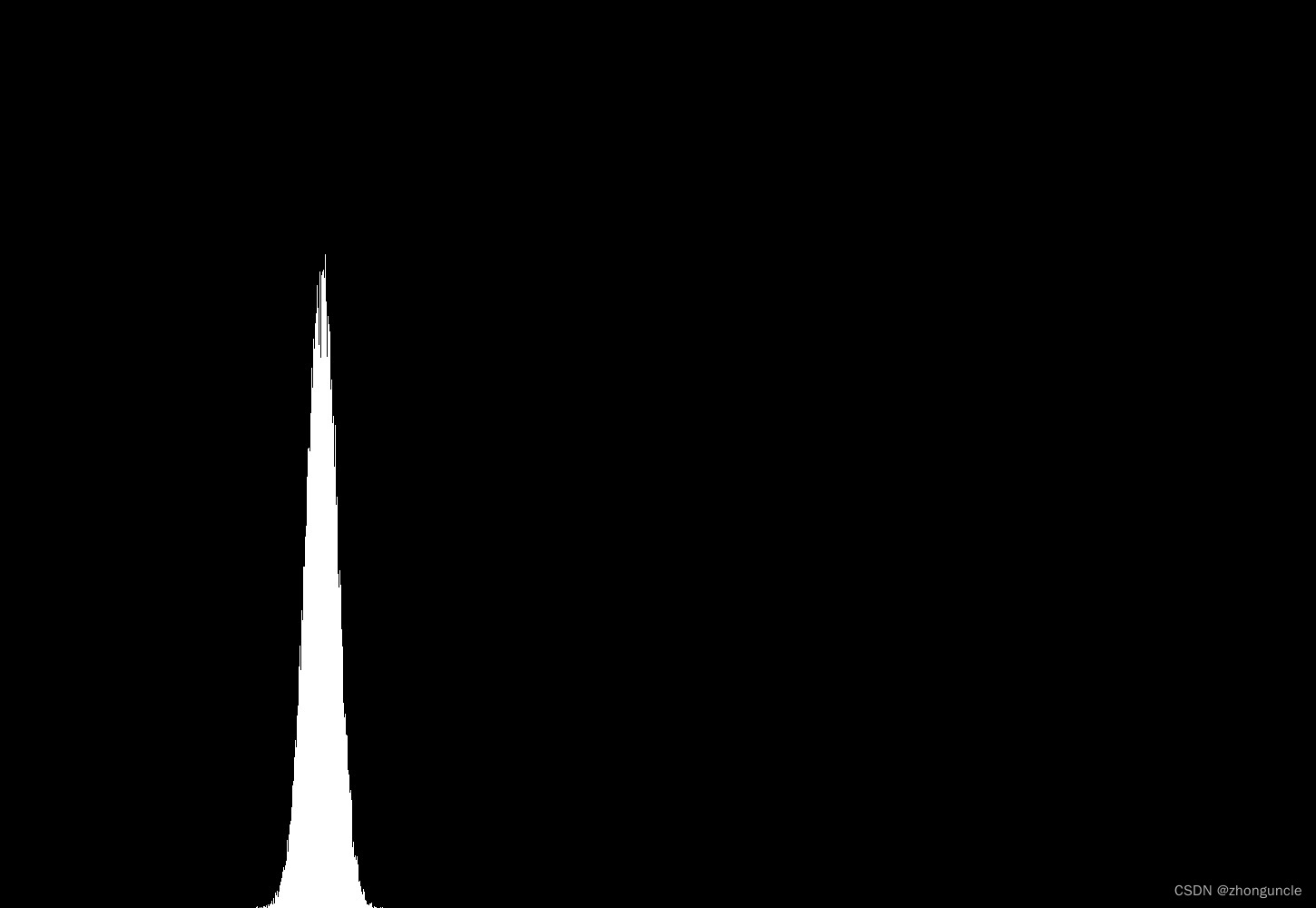
就很近似正态分布曲线了，但是这样太尖了，为了更明显一些，我们来将其“拉宽压扁”。方法是将第二个大的for循环修改成如下：
for (int i=0; i<width; i++) {
// sumArr[i]/2是为了压缩图像
for (int j=height-1; j>=height-sumArr[i]/2; j--) {
//拉宽图像
for (int k=0; k<10; k++) {
output[j*width+i*10+k]=256;
}
}
}
也就是变成 2x10 个像素表示一个样本，下面全都是按照这种缩放来展示图像。这时候图像如下：
这时候和很像标准正态分布的图像了。如果你想真的实现标准正态分布的图像，那就加上计算方差和样本均值的部分，多几步就可以了。
非均匀分布下，点数之和的概率
接下来我们来尝试一下非均匀分布的概率的图像。这个一开始难到我了，我不知道如何让每个值的概率不同，但是很快就反应过来了，这不就是箱子（数组）里抓小球（元素）嘛，那修改一下数组的元素数量和值即可，所以这时候样本空间的数组为：
int a[] = {1,1,1,1,1,2,3,4,5,6};
1有五个，也就是说1的概率为 0.5 ，其余值均为 0.1。
这时候也需要修改一下源代码，不仅是因为元素数量变了，随机值范围也得变，更是要考虑到多种测试的情况，要将其写的通用一些，所以修改成以下样式：
int main() {
int width = 1700;
int height = 1000;
int a[] = {1,1,1,1,1,2,3,4,5,6};
//count用来统计样本空间的大小，这样就不用手动去下面依次修改了
int count = sizeof(a)/sizeof(int);
int* sumArr = new int[width];
int* output = new int[width*height];
for (int i=0; i<height*30; i++) {
int temp = a[random()%count];
for (int j=0; j<100; j++) {
temp = temp + a[random()%count];
}
sumArr[temp] = sumArr[temp]+1;
}
for (int i=0; i<width; i++) {
// sumArr[i]/2是为了压缩图像
for (int j=height-1; j>=height-sumArr[i]/2; j--) {
//拉宽图像
for (int k=0; k<10; k++) {
output[j*width+i*10+k]=256;
}
}
}
writePPMImage(output, width, height, "output.ppm", 256);
delete[] sumArr;
delete[] output;
return 0;
}
这时候生成的图像如下：
可以看到，还是符合正态分布曲线的，并没有因为1的概率很大就导致图像发生变化。
那再极限一些呢？如果1的概率高达 99% 呢？
遗憾的是，要使1的概率高达 99%，需要样本空间数组有 500 个元素，这会导致一些资源分配错误，就试试看1的概率为 95% 的情况，那么这个数组如下（这里列出这个数组是为了读者方便可以复制下来自己试试看）：
int a[] = {
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, //40个
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, //40个
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, //40个
2,3,4,5,6,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, //15个1
};
这时候这个图像如下：
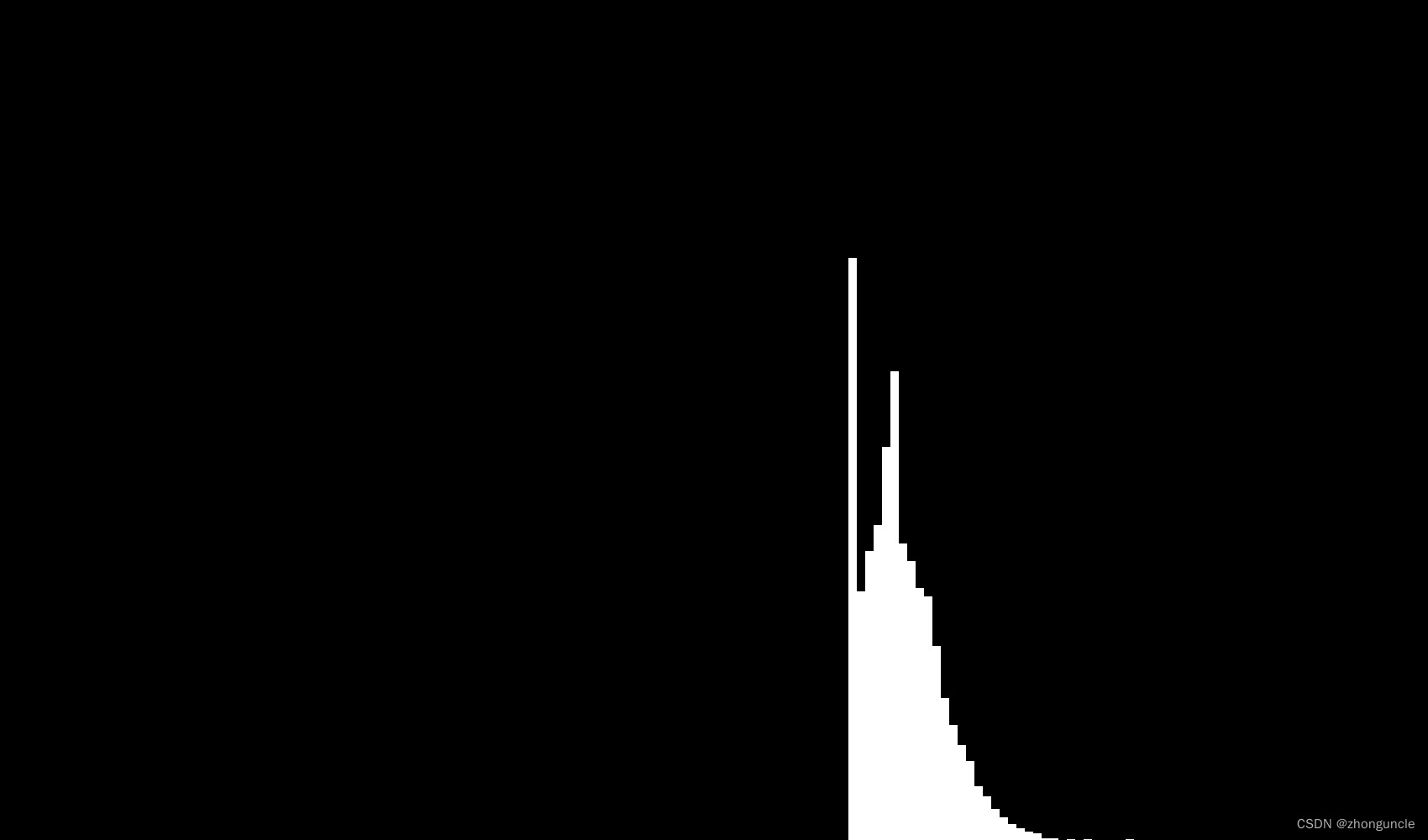
可以看到，最小值1+1=2的样本最多，但是右边还是比较像正态分布的一半的，那如果加大累加次数呢？比如说从 100 次提升到 1000 次（样本数量降低到 1 万次），这时候的图像如下：
由于可能性太多，所以这里的图像尺寸为 17000x1000px，有点看不清，所以我裁了图像的部分出来：
可以看到，最终还是符合正态分布曲线的，这也正是中心极限定理。
完整代码
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include <algorithm>
using namespace std;
void
writePPMImage(int* data, int width, int height, const char *filename, int maxIterations)
{
FILE *fp = fopen(filename, "wb");
// write ppm header
fprintf(fp, "P6
");
fprintf(fp, "%d %d
", width, height);
fprintf(fp, "255
");
for (int i = 0; i < width*height; ++i) {
float mapped = pow( std::min(static_cast<float>(maxIterations), static_cast<float>(data[i])) / 256.f, .5f);
unsigned char result = static_cast<unsigned char>(255.f * mapped);
for (int j = 0; j < 3; ++j)
fputc(result, fp);
}
fclose(fp);
printf("Wrote image file %s
", filename);
}
int main() {
//输出图像的尺寸
//图像会随着累加次数右移，所以增加累加次数的时候要把输出图像的宽度扩大一些
int width = 17000;
int height = 1000;
int a[] = {
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, //40个
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, //40个
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, //40个
2,3,4,5,6,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, //15个
};
//count用来统计样本空间的大小，这样就不用手动去下面依次修改了
int count = sizeof(a)/sizeof(int);
//用来存放各种点数之和的数量多数组，这里不要声明空数组，因为一些编译器会给没有值的元素分配一些很奇怪的值，导致运行错误（不像C语言是默认为0）
int* sumArr = new int[width];
//用来存放最后输出图像的像素色彩信息的数组
int* output = new int[width*height];
//样本量为10x1000=10000，也就是取1万次点数之和
for (int i=0; i<height*10; i++) {
//获取到一个随机点数。模6表示随机值范围是0～count，刚好对应前面数组a的每个元素
int temp = a[random()%count];
//下面的循环将会累加1000次，也就是表示多少个骰子点数之和
for (int j=0; j<1000; j++) {
temp = temp + a[random()%count];
}
sumArr[temp] = sumArr[temp]+1;
}
//因为输出图像的时候，条状图是从底部开始的，所以写这样的一个转换
for (int i=0; i<width; i++) {
// sumArr[i]/2是为了压缩图像
for (int j=height-1; j>=height-sumArr[i]/2; j--) {
//拉宽图像
for (int k=0; k<10; k++) {
output[j*width+i*10+k]=256;
}
}
}
//输出图像
writePPMImage(output, width, height, "mandelbrot-serial.ppm", 256);
delete[] sumArr;
delete[] output;
return 0;
}
蛮有意思的，希望能帮到有需要的人～
风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。
站长推荐
- U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 - stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程） - SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权 - 【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》 - 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效)