您现在的位置是：首页 >技术教程 >【数据结构】线性表之栈、队列网站首页技术教程
【数据结构】线性表之栈、队列
前言
前面两篇文章讲述了关于线性表中的顺序表与链表，这篇文章继续讲述线性表中的栈和队列。
这里讲述的两种线性表与前面的线性表不同，只允许在一端入数据，一段出数据，详细内容请看下面的文章。
顺序表与链表两篇文章的链接：
线性表之顺序表
线性表之链表
注意： 本文提到的效率全部为空间复杂度！！！！
一、栈
1. 栈的概念
栈:一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO (Last ln FirstOut)的原则.
入栈:栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据也在栈顶。
2. 栈的结构
栈的结构决定了栈只能在栈顶入数据，栈顶出数据，并且遵循着后进先出的原则。
2.1 选择数据结构完成栈（数组 or 链表)
2.1.1 数组
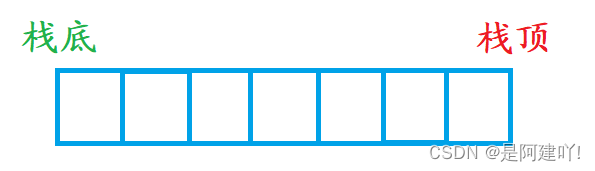
前面学习过顺序表就能知道，数组只有尾插和尾删的效率高为 O(1) , 而靠近头的位置的插入删除的效率比较低为O(N)。
而对于栈这种只能在栈顶插入、删除的数据结构可谓是完美契合数组的优点。
2.1.2 链表
前面学习过链表就可以知道，对于单链表的头插、头删的效率非常高为 O(1) , 而它的尾插、尾删需要找尾，效率比较低为 O(N)。
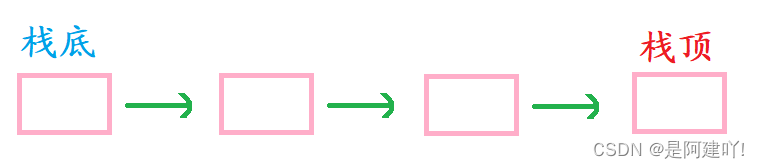
若以单链表的头为栈底，尾为栈顶，则入栈、出栈相当于单链表的尾插、尾删效率并不高。
显然这不是我们的最佳选项，但是若用一个变量记录尾的情况下，尾插、尾删的效率也可以达到O(1)。
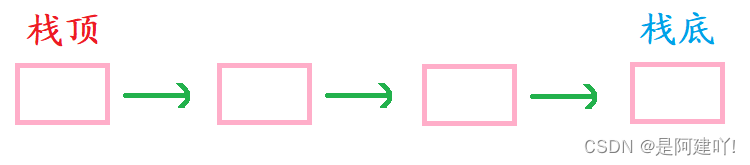
若以单链表的头为栈顶，尾为栈底，则入栈、出栈相当于单链表的头插、头删效率非常高为O(1)。
这里与前面的数组差不多，也是栈的操作完全契合单链表的优点。
栈能够使用单链表实现，当然也可以用带头双向循环链表实现，但是我认为这里使用带头双向循环链表有点大炮打蚊子，大材小用的感觉。
2.1.3 我选择用数组完成栈
为什么这里选择数组完成栈呢？
明明数组容量不足时扩容需要消耗，而链表没有这个消耗，为什么不用链表？
原因有以下几点：
- 由于数组物理结构上是连续的，缓存命中率高，访问效率高。
- 相比链表，数组只需要存储数据，而链表每一个节点还需要存下一个节点的地址。
- 虽然数组扩容有消耗，但是链表每次申请节点的时候也会有消耗。
2.2 栈的操作
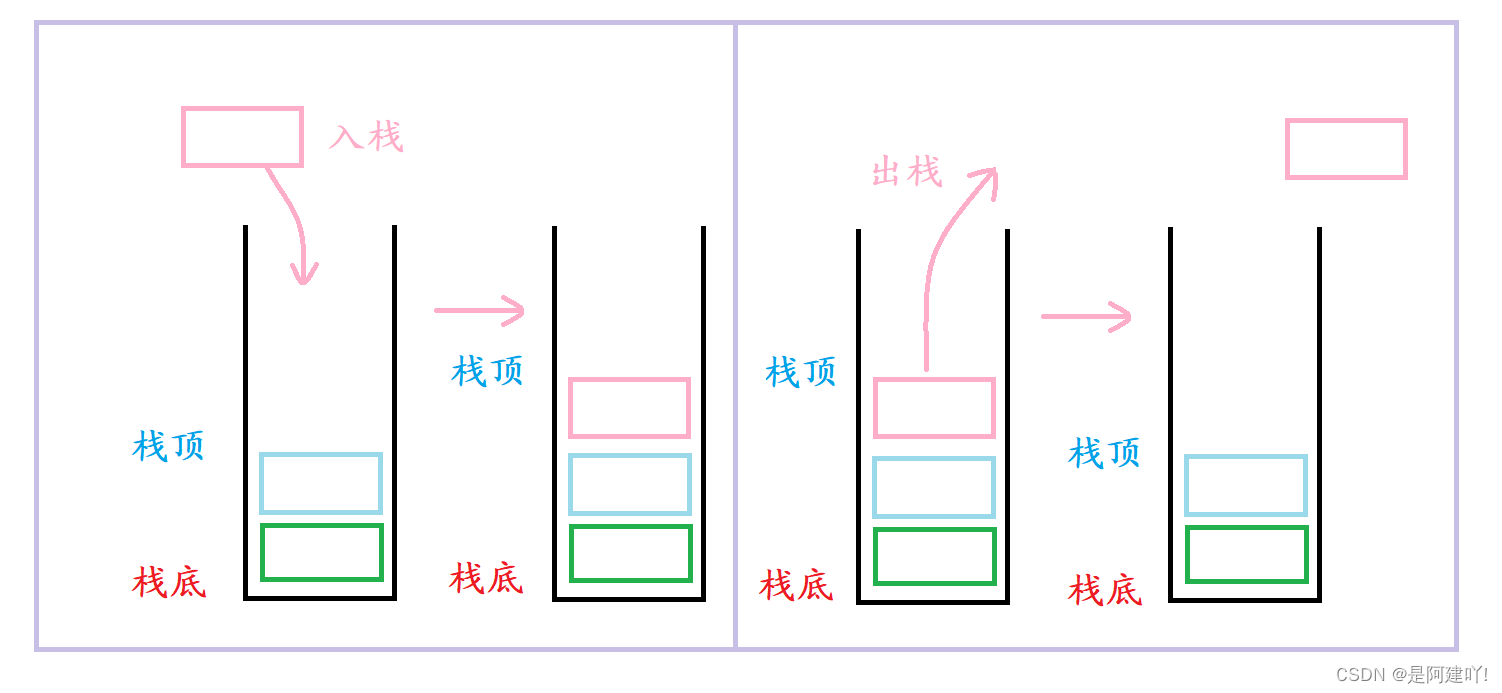
3. 栈的实现
Stack.h头文件的实现
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top; // 栈顶
int capacity; // 容量
}Stack;
// 初始化栈
void StackInit(Stack* ps);
// 入栈
void StackPush(Stack* ps, STDataType data);
// 出栈
void StackPop(Stack* ps);
// 获取栈顶元素
STDataType StackTop(Stack* ps);
// 获取栈中有效元素个数
int StackSize(Stack* ps);
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0
int StackEmpty(Stack* ps);
// 销毁栈
void StackDestroy(Stack* ps);
Stack.c文件的实现
3.1 初始化栈
栈的初始化将传入函数的结构体进行初始化：
a. 栈顶初始化的时候注意有两种情况:
1. top指向栈顶元素
2. top指向栈顶元素的后面一个位置
当然都可以，我选择 1 仅仅方便我自己理解
b. 是否在初始化的时候给栈申请部分空间
当然都可以，我这里选择不申请空间，在后面用realloc函数申请和扩容空间。
// 初始化栈
void StackInit(Stack* ps)
{
assert(ps);
ps->capacity = 0;
//ps->top = -1; //top指向栈顶
ps->top = 0; //top指向栈顶的后面一个元素
ps->a = NULL;
}
3.2 入栈
当数据入栈时需要判断栈是否为满，若为满则需要扩容，这里的StackFull函数其实并没有必要，由于栈只有尾插这一个插入操作不需要复用扩容操作，所以可以直接写在入栈操作中。
注意：
当realloc()函数的参数为NULL时，其作用与malloc()函数的作用一样。
void StackFull(Stack* ps)
{
assert(ps);
int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newcapacity);
if (tmp == NULL)
{
perror("realloc");
return;
}
ps->a = tmp;
ps->capacity = newcapacity;
}
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
if (ps->capacity == ps->top)
StackFull(ps);
ps->a[ps->top] = data;
ps->top++;
}
3.3 判空
前面假设了top是指向栈顶元素后面一个位置，所以当 top 指向 0 的时候栈是空的。
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0
int StackEmpty(Stack* ps)
{
assert(ps);
return ps->top == 0;
}
3.4 出栈
执行出栈操作时，栈不能为空，且只需要 top-- ， 不需要将其数据抹除。
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
assert(!StackEmpty(ps));
//栈为空，则不能继续出栈
ps->top--;
}
3.5 取栈顶元素
与出栈操作一样，取栈顶元素时，栈不能为空。
且top是指向栈顶元素后面一个位置，所以取栈顶元素时取的是 top - 1 指向的元素。
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
assert(!StackEmpty(ps));
//栈为空，则无栈顶元素
return ps->a[ps->top - 1];
}
3.6 获取栈中有效元素个数
由于top是指向栈顶元素的下一个位置，而元素个数正好是下标 + 1 ，也就是top。
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->top; //由于top是指向栈顶元素的下一个位置
//而元素个数正好是下标 + 1 ，也就是top
}
3.7 销毁栈
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->capacity = 0;
ps->top = 0;
}
4. 整体代码的实现
#include "Stack.h"
// 初始化栈
void StackInit(Stack* ps)
{
assert(ps);
ps->capacity = 0;
ps->top = 0; //top指向栈顶的后面一个元素
ps->a = NULL;
}
void StackFull(Stack* ps)
{
assert(ps);
int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newcapacity);
if (tmp == NULL)
{
perror("realloc");
return;
}
ps->a = tmp;
ps->capacity = newcapacity;
}
// 入栈
void StackPush(Stack* ps, STDataType data)
{
assert(ps);
if (ps->capacity == ps->top)
StackFull(ps);
ps->a[ps->top] = data;
ps->top++;
}
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0
int StackEmpty(Stack* ps)
{
assert(ps);
return ps->top == 0;
}
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
assert(!StackEmpty(ps));
//栈为空，则不能继续出栈
ps->top--;
}
// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
assert(!StackEmpty(ps));
//栈为空，则无栈顶元素
return ps->a[ps->top - 1];
}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
return ps->top; //由于top是指向栈顶元素的下一个位置
//而元素个数正好是下标 + 1 ，也就是top
}
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->capacity = 0;
ps->top = 0;
}
二、队列
1. 队列的概念
队列:只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有 先进先出 FIFO(First In First Out) 的原则。
入队列:进行插入操作的一端称为队尾
出队列:进行删除操作的一端称为队头
2. 队列的结构
2.1 选择数据结构完成队列（数组 or 链表)
2.1.1 数组
前面学习过顺序表就能知道，数组只有尾插和尾删的效率高为 O(1) , 而靠近头的位置的插入删除的效率比较低为O(N)。
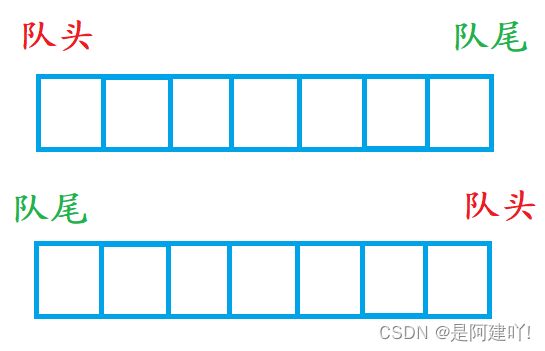
而对于队列这种只能在队尾插入、对头删除的数据结构，无论队头和队尾定义在哪，使用数组完成必定会有头删或头插，会使得队列的效率降低，所以不建议使用数组完成。
2.1.2 链表
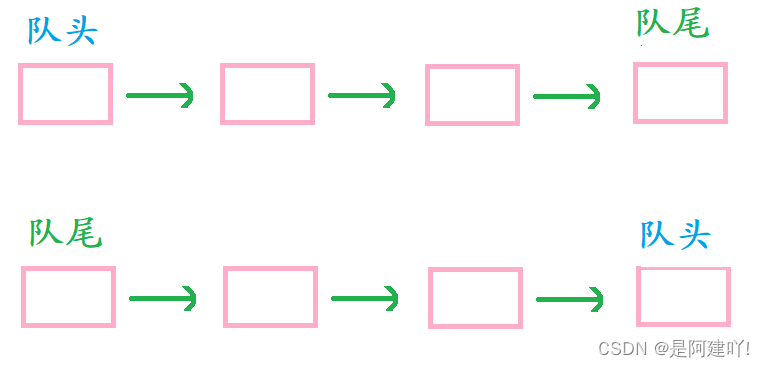
前面学习过链表就可以知道，对于单链表的头插、头删的效率非常高为 O(1) , 而它的尾插、尾删需要找尾，效率比较低为 O(N)。
(1)若以单链表的头为队头，尾为队尾，则入队列、出队列相当于单链表的尾插、头删效率并不高。
(2)若以单链表的头为队尾，尾为队头，则入队列、出队列相当于单链表的头插、尾删效率并不高。
虽然两种情况都有一种操作效率为O(N) , 但是这两种情况都是与尾有关的操作，
所以只要在结构体中定一个记录尾的成员，那么尾插、尾删的效率就能达到O(1).
2.1.3 我选择用链表完成队列
为什么这里选择链表完成队列？
通过上面的讲述原因已经显而易见了。
原因如下：
由于无论怎么改造数组都会有一个操作效率为 O(N),而链表只需要改变结构体，使其多一个指向尾的成员，就能使队列的插入、删除的操作效率为O(1).
3. 队列的实现
Queue.h头文件的实现
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef int QDataType;
// 链式结构：表示队列
typedef struct QListNode
{
struct QListNode* next;
QDataType data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* front;
QNode* rear; //指向队列最后一个元素的后面
int size;
}Queue;
// 初始化队列
void QueueInit(Queue* q);
// 队尾入队列
void QueuePush(Queue* q, QDataType data);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 获取队列队尾元素
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数
int QueueSize(Queue* q);
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0
int QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);
Queue.c文件的实现
3.1 初始化队列
这里队列的front指向队头，rear指向队尾。
当队列为空的时候，那么front和rear 都是指向 NULL。
// 初始化队列
void QueueInit(Queue* q)
{
q->front = NULL;
q->rear = NULL;
q->size = 0;
}
3.2 队尾入队列
由于使用链表实现队列，插入时需要申请一个节点。
入队列分为两种情况：
- 队列为空时，需要改变队头、队尾的指针。
- 队列不为空时，只需要将新节点接到队尾，并将尾指针向后移动即可。
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc");
return;
}
newnode->next = NULL;
newnode->data = data;
if (q->front == NULL) //分队列是否有元素两种情况
{ //队列为空
assert(q->rear == NULL);
q->front = newnode;
q->rear = newnode;
}
else
{ //队列不为空
q->rear->next = newnode;
q->rear = newnode;
}
q->size++;//入队列，队列长度加一
}
3.3 判空
当队列中的头、尾指针都指向NULL的时候为队列为空。
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0
int QueueEmpty(Queue* q)
{
assert(q);
return q->front == NULL && q->rear == NULL;
}
3.4 队头出队列
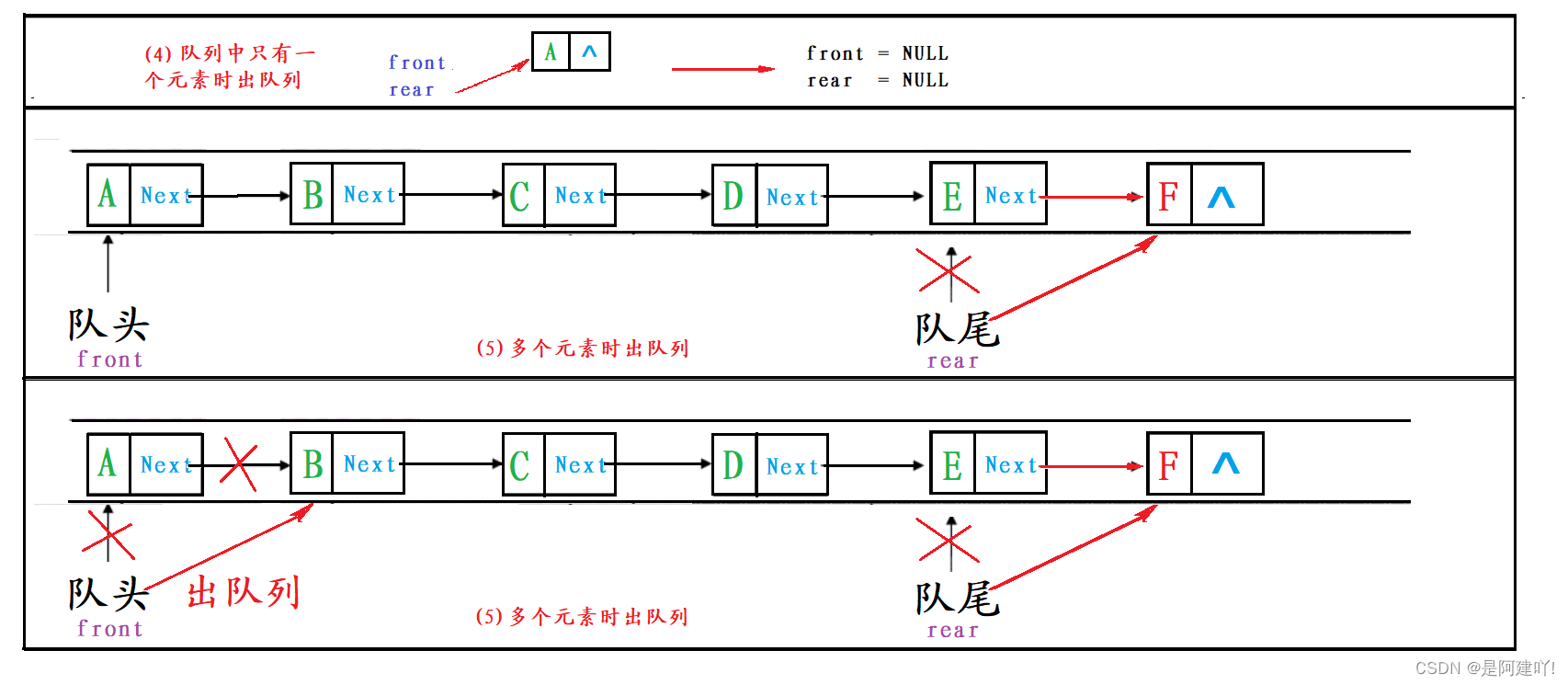
出队列分为两种情况：
- 队列中只有一个元素时：删除最后一个节点，并将
front和rear指向NULL。 - 队列中有多个元素时：删除
front指向的节点，并将front向后移动。
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
//出队列时，队列不能为空
assert(!QueueEmpty(q));
//当队列中只有一个元素的时候，不仅仅头指针需要改变，尾指针也需要改变
//因为当删除最后一个元素时，首指针释放当前节点，并向后移动，而尾指针并没有移动
//当释放后若在插入元素时，尾指针会造成野指针的情况
if (q->front->next == NULL)
{
QNode* del = q->front;
q->front = NULL;
q->rear = NULL;
free(del);
}
else
{
QNode* del = q->front;
q->front = q->front->next;
free(del);
}
q->size--;
}
3.5 获取队列头部元素
front 指向的节点存储着头部元素。
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);
//获取队列头部元素时，队列不能为空
assert(!QueueEmpty(q));
return q->front->data;
}
3.6 获取队列队尾元素
rear 指向的节点存储着尾元素。
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(q);
//获取队列头部元素时，队列不能为空
assert(!QueueEmpty(q));
return q->rear->data;
}
3.7 获取队列中有效元素个数
结构体中的 size 存储着队列中的有效元素个数
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
//结构体中定义了一个size
//而这里遍历链表得到个数，效率低O(N)
/*int size = 0; 不要用
QNode* cur = q->front;
while (cur != q->rear)
{
size++;
q->front = q->front->next;
}*/
return q->size;
}
3.8 销毁队列
销毁队列与前面销毁单链表相同，需要将每一个节点都释放。
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->front;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
}
4. 整体代码的实现
// 初始化队列
void QueueInit(Queue* q)
{
q->front = NULL;
q->rear = NULL;
q->size = 0;
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc");
return;
}
newnode->next = NULL;
newnode->data = data;
if (q->front == NULL) //分队列是否有元素两种情况
{
assert(q->rear == NULL);
q->front = newnode;
q->rear = newnode;
}
else
{
q->rear->next = newnode;
q->rear = newnode;
}
q->size++;//入队列，队列长度加一
}
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0
int QueueEmpty(Queue* q)
{
assert(q);
return q->front == NULL && q->rear == NULL;
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
//出队列时，队列不能为空
assert(!QueueEmpty(q));
//当队列中只有一个元素的时候，不仅仅头指针需要改变，尾指针也需要改变
//因为当删除最后一个元素时，首指针释放当前节点，并向后移动，而尾指针并没有移动
//当释放后若在插入元素时，尾指针会造成野指针的情况
if (q->front->next == NULL)
{
QNode* del = q->front;
q->front = NULL;
q->rear = NULL;
free(del);
}
else
{
QNode* del = q->front;
q->front = q->front->next;
free(del);
}
q->size--;
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);
//获取队列头部元素时，队列不能为空
assert(!QueueEmpty(q));
return q->front->data;
}
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(q);
//获取队列头部元素时，队列不能为空
assert(!QueueEmpty(q));
return q->rear->data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
//结构体中定义了一个size
//而这里遍历链表得到个数，效率低
/*int size = 0; 不要用
QNode* cur = q->front;
while (cur != q->rear)
{
size++;
q->front = q->front->next;
}*/
return q->size;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->front;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
}
结尾
注意： 本文提到的效率全部为空间复杂度！！！！
如果有什么建议和疑问，或是有什么错误，大家可以在评论区中提出。
希望大家以后也能和我一起进步！！??
如果这篇文章对你有用的话，希望大家给一个三连！！??
站长推荐
- SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权 - stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程） - U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 - 【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》 - 【云原生进阶之容器】第六章容器网络6.6.1--Cilium网络方案概述
【云原生进阶之容器】第六章容器网络6.6.1--Cilium网络方案概述