您现在的位置是:首页 >技术杂谈 >Python模糊控制网站首页技术杂谈
Python模糊控制
Python模糊控制
概念和术语
模糊逻辑(Fuzzy Logic)是一种方法论,其基础是可以在连续统一体上表达某物的“真实性”。这就是说某事不是真或假,而是部分正确或部分错误。
模糊变量(fuzzy variable)具有明确的值(crisp value),该值在预定义的域(在模糊逻辑术语中,称为宇宙(universe))上取一些数字。明确的值是我们如何使用普通数学来思考变量。例如,如果我的模糊变量是给某人多少小费,它的范围将是 0 到 25%,并且它可能采用 15% 的清晰值。
模糊变量也有几个用于描述变量的术语。这些项合在一起就是模糊集(fuzzy set),可以用来描述模糊变量的“模糊值”。这些术语通常是形容词,如“差”、“平庸”和“好”。每个术语都有一个隶属函数(membership function),它定义了一个明确的值如何在 0 到 1 的范围内映射到该术语。本质上,它描述了某物“有多好”。
所以,回到小费的例子,一个“好小费”可能有一个成员函数,它有一个介于 15% 和 25% 之间的非零值,其中 25% 是一个“完全好的小费”(即,它的成员资格是 1.0)并且15% 是一个“勉强好的小费”(即它的成员是 0.1)。
模糊控制系统使用一组规则链接模糊变量。这些规则只是描述一个或多个模糊变量如何与另一个相关的映射。这些是用 IF-THEN 语句表示的; IF 部分称为前件(antecedent ),THEN 部分称为后件(consequent)。在小费示例中,一条规则可能是“如果服务好,那么小费也不错”。与如何使用规则根据前提值计算结果值相关的精确数学超出了本入门指南的范围。
小费问题
“小费问题”通常用于说明模糊逻辑原理从一组紧凑、直观的专家规则中生成复杂行为的能力。
以小费为例,如果我们要创建一个控制器来估计我们应该在餐厅给的小费,我们可以这样构建它:
-
前导网络(输入)[Antecednets (Inputs)]
- 服务
- Universe(即明确的值范围):女服务员的服务有多好,从 1 到 10 打分?[service Universe (ie, crisp value range): How good was the service of the waitress, on a scale of 1 to 10?]
- 模糊集(即模糊值范围):差、可接受、惊人[Fuzzy set (ie, fuzzy value range): poor, acceptable, amazing]
- 食物
- Universe:从 1 到 10 打分,食物有多好吃?[food quality Universe: How tasty was the food, on a scale of 1 to 10? ]
- 模糊集:坏的,体面的,伟大的 [Fuzzy set: bad, decent, great ]
- 服务
-
结果(输出)[Consequents (Outputs) ]
- Universe:我们应该给多少小费,从 0% 到 25% [ tip Universe: How much should we tip, on a scale of 0% to 25%]
- 模糊集:低、中、高 [Fuzzy set: low, medium, high]
-
Rules
- 如果服务好或食品质量好,那么小费就会很高。[IF the service was good or the food quality was good, THEN the tip will be high. ]
- 如果服务是平均的,那么小费将是中等的。[IF the service was average, THEN the tip will be medium.]
- 如果服务很差而且食物质量很差,那么小费就会很低。[IF the service was poor and the food quality was poor THEN the tip will be low. ]
-
Usage
- If I tell this controller that I rated: 如果我告诉这个控制器我评价了:
- the service as 9.8, and 服务为 9.8,和
- the quality as 6.5, 质量为6.5,
- it would recommend I leave: 它会建议我给出的小费参考:
- a 20.2% tip. 20.2% 的小费。
- If I tell this controller that I rated: 如果我告诉这个控制器我评价了:
代码实战
1.选择输入输出模糊集
2.定义输入输出隶属度函数(不同的隶属度函数,会导致不同的控制特性)
3.建立模糊控制表
4.建立模糊控制规则
5.模糊推理
6.反模糊化
7.输出结果绘制结果3D图
例子:输入为服务(service)和质量(quality)两个参数,输出为得到的小费(tip)
输入变量
关于用餐时给多少小费的决定有许多变量。考虑其中两个:
quality:食物的质量service:服务质量
输出变量
输出变量只是小费金额,以百分比表示:
tip: 添加为小费的账单百分比
代码逻辑
出于讨论的目的,假设我们需要输入变量和输出变量的“高”、“中”和“低”隶属函数。这些在 scikit-fuzzy 中定义如下
import numpy as np
import skfuzzy as fuzz
import matplotlib.pyplot as plt
# Generate universe variables
# * Quality and service on subjective ranges [0, 10]
# * Tip has a range of [0, 25] in units of percentage points
x_qual = np.arange(0, 11, 1)
x_serv = np.arange(0, 11, 1)
x_tip = np.arange(0, 26, 1)
# Generate fuzzy membership functions
qual_lo = fuzz.trimf(x_qual, [0, 0, 5])
qual_md = fuzz.trimf(x_qual, [0, 5, 10])
qual_hi = fuzz.trimf(x_qual, [5, 10, 10])
serv_lo = fuzz.trimf(x_serv, [0, 0, 5])
serv_md = fuzz.trimf(x_serv, [0, 5, 10])
serv_hi = fuzz.trimf(x_serv, [5, 10, 10])
tip_lo = fuzz.trimf(x_tip, [0, 0, 13])
tip_md = fuzz.trimf(x_tip, [0, 13, 25])
tip_hi = fuzz.trimf(x_tip, [13, 25, 25])
# Visualize these universes and membership functions
fig, (ax0, ax1, ax2) = plt.subplots(nrows=3, figsize=(8, 9))
ax0.plot(x_qual, qual_lo, 'b', linewidth=1.5, label='Bad')
ax0.plot(x_qual, qual_md, 'g', linewidth=1.5, label='Decent')
ax0.plot(x_qual, qual_hi, 'r', linewidth=1.5, label='Great')
ax0.set_title('Food quality')
ax0.legend()
ax1.plot(x_serv, serv_lo, 'b', linewidth=1.5, label='Poor')
ax1.plot(x_serv, serv_md, 'g', linewidth=1.5, label='Acceptable')
ax1.plot(x_serv, serv_hi, 'r', linewidth=1.5, label='Amazing')
ax1.set_title('Service quality')
ax1.legend()
ax2.plot(x_tip, tip_lo, 'b', linewidth=1.5, label='Low')
ax2.plot(x_tip, tip_md, 'g', linewidth=1.5, label='Medium')
ax2.plot(x_tip, tip_hi, 'r', linewidth=1.5, label='High')
ax2.set_title('Tip amount')
ax2.legend()
# Turn off top/right axes
for ax in (ax0, ax1, ax2):
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
plt.tight_layout()
plt.show()
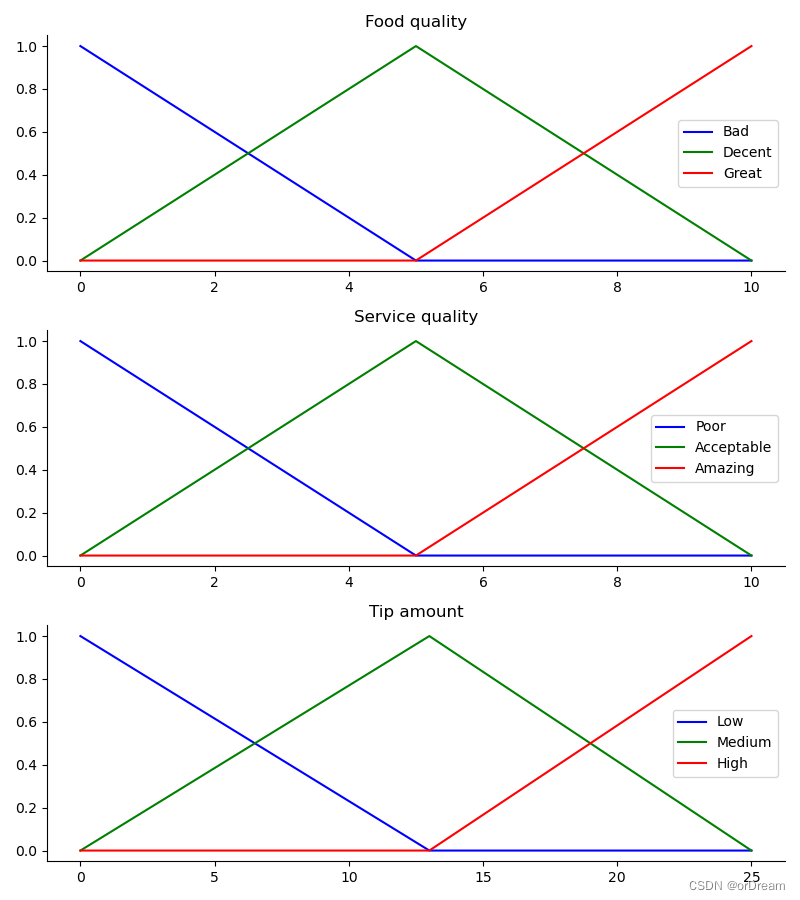
模糊规则
现在,为了使这些三角形有用,我们定义了输入和输出变量之间的模糊关系。出于我们示例的目的,请考虑三个简单的规则:
- 如果食物不好或服务很差,那么小费会很低
- 如果服务可以接受,那么小费将是中等
- 如果食物很棒或服务很棒,那么小费就会很高。
| 服务质量小费食品质量 | Bad | Decent | Great |
|---|---|---|---|
| Poor | Low | Low | Medium |
| Acceptable | Low | Medium | High |
| Amazing | Medium | High | High |
大多数人会同意这些规则,但规则很模糊。将不精确的规则映射到明确的、可操作的提示中是一项挑战。这是模糊逻辑擅长的任务。
规则应用
在以下情况下提示是什么:
- 食品质量为 6.5
- 服务质量是9.8
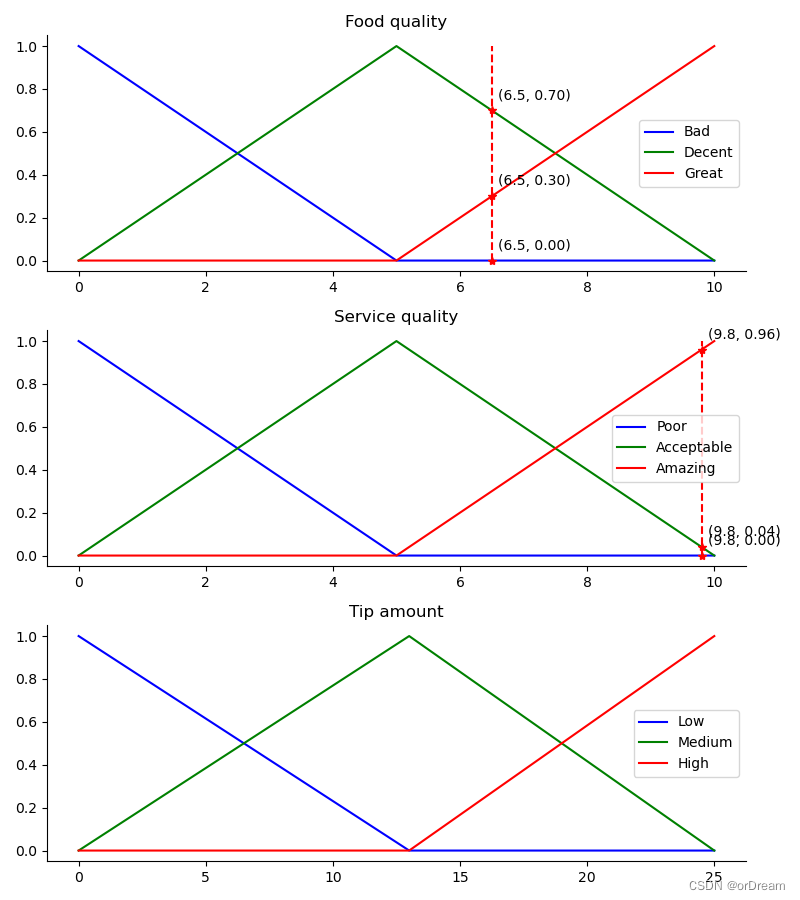
# We need the activation of our fuzzy membership functions at these values.
# The exact values 6.5 and 9.8 do not exist on our universes...
# This is what fuzz.interp_membership exists for!
qual_level_lo = fuzz.interp_membership(x_qual, qual_lo, 6.5)
qual_level_md = fuzz.interp_membership(x_qual, qual_md, 6.5)
qual_level_hi = fuzz.interp_membership(x_qual, qual_hi, 6.5)
serv_level_lo = fuzz.interp_membership(x_serv, serv_lo, 9.8)
serv_level_md = fuzz.interp_membership(x_serv, serv_md, 9.8)
serv_level_hi = fuzz.interp_membership(x_serv, serv_hi, 9.8)
# Now we take our rules and apply them. Rule 1 concerns bad food OR service.
# The OR operator means we take the maximum of these two.
active_rule1 = np.fmax(qual_level_lo, serv_level_lo)
# Now we apply this by clipping the top off the corresponding output
# membership function with `np.fmin`
tip_activation_lo = np.fmin(active_rule1, tip_lo) # removed entirely to 0
# For rule 2 we connect acceptable service to medium tipping
tip_activation_md = np.fmin(serv_level_md, tip_md)
# For rule 3 we connect high service OR high food with high tipping
active_rule3 = np.fmax(qual_level_hi, serv_level_hi)
tip_activation_hi = np.fmin(active_rule3, tip_hi)
tip0 = np.zeros_like(x_tip)
# Visualize this
fig, ax0 = plt.subplots(figsize=(8, 3))
ax0.fill_between(x_tip, tip0, tip_activation_lo, facecolor='b', alpha=0.7)
ax0.plot(x_tip, tip_lo, 'b', linewidth=0.5, linestyle='--', )
ax0.fill_between(x_tip, tip0, tip_activation_md, facecolor='g', alpha=0.7)
ax0.plot(x_tip, tip_md, 'g', linewidth=0.5, linestyle='--')
ax0.fill_between(x_tip, tip0, tip_activation_hi, facecolor='r', alpha=0.7)
ax0.plot(x_tip, tip_hi, 'r', linewidth=0.5, linestyle='--')
ax0.set_title('Output membership activity')
# Turn off top/right axes
for ax in (ax0,):
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
plt.tight_layout()
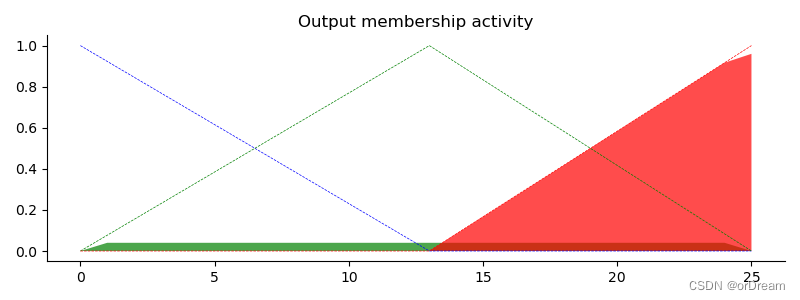
规则聚合
在已知每个输出隶属函数的活动的情况下,必须组合所有输出隶属函数。这通常是使用最大运算符完成的。此步骤也称为聚合。
去模糊化 (Defuzzification)
最后,为了得到真实世界的答案,我们从模糊隶属函数的世界回到清晰的逻辑。出于本示例的目的,将使用质心方法。
结果显示小费为20.22%
# Aggregate all three output membership functions together
aggregated = np.fmax(tip_activation_lo,
np.fmax(tip_activation_md, tip_activation_hi))
# Calculate defuzzified result
tip = fuzz.defuzz(x_tip, aggregated, 'centroid')
tip_activation = fuzz.interp_membership(x_tip, aggregated, tip) # for plot
# Visualize this
fig, ax0 = plt.subplots(figsize=(8, 3))
ax0.plot(x_tip, tip_lo, 'b', linewidth=0.5, linestyle='--', )
ax0.plot(x_tip, tip_md, 'g', linewidth=0.5, linestyle='--')
ax0.plot(x_tip, tip_hi, 'r', linewidth=0.5, linestyle='--')
ax0.fill_between(x_tip, tip0, aggregated, facecolor='Orange', alpha=0.7)
ax0.plot([tip, tip], [0, tip_activation], 'k', linewidth=1.5, alpha=0.9)
ax0.set_title('Aggregated membership and result (line)')
# Turn off top/right axes
for ax in (ax0,):
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
plt.tight_layout()
plt.show()
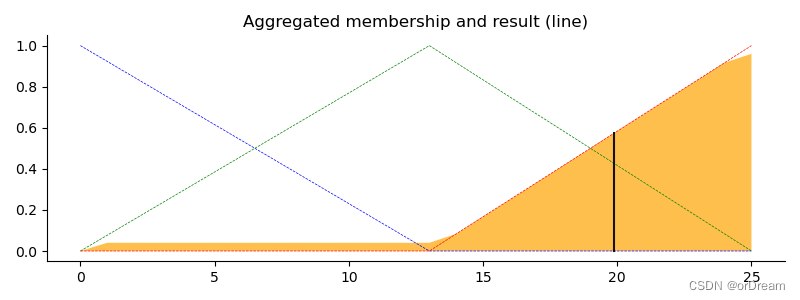
最后的思考
模糊系统的强大功能是允许基于稀疏的规则系统以最小的开销进行复杂、直观的行为。请注意,我们的隶属函数域是粗略的,仅定义为整数,但 fuzz.interp_membership 允许有效分辨率按需增加。该系统可以响应输入中任意小的变化,并且处理负担最小。
reference
@misc{BibEntry2023May,
title = {{General examples {ifmmode—else extemdashfi} skfuzzy v0.2 docs}},
year = {2023},
month = may,
note = {[Online; accessed 19. May 2023]},
url = {https://pythonhosted.org/scikit-fuzzy/auto_examples/index.html}
}






 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结