您现在的位置是：首页 >学无止境 >环环相扣，循环不止：深入解析循环队列网站首页学无止境

本盘博客会讲解力扣“622. 设计循环队列”的解题思路，这是题目链接。

先来审下题：

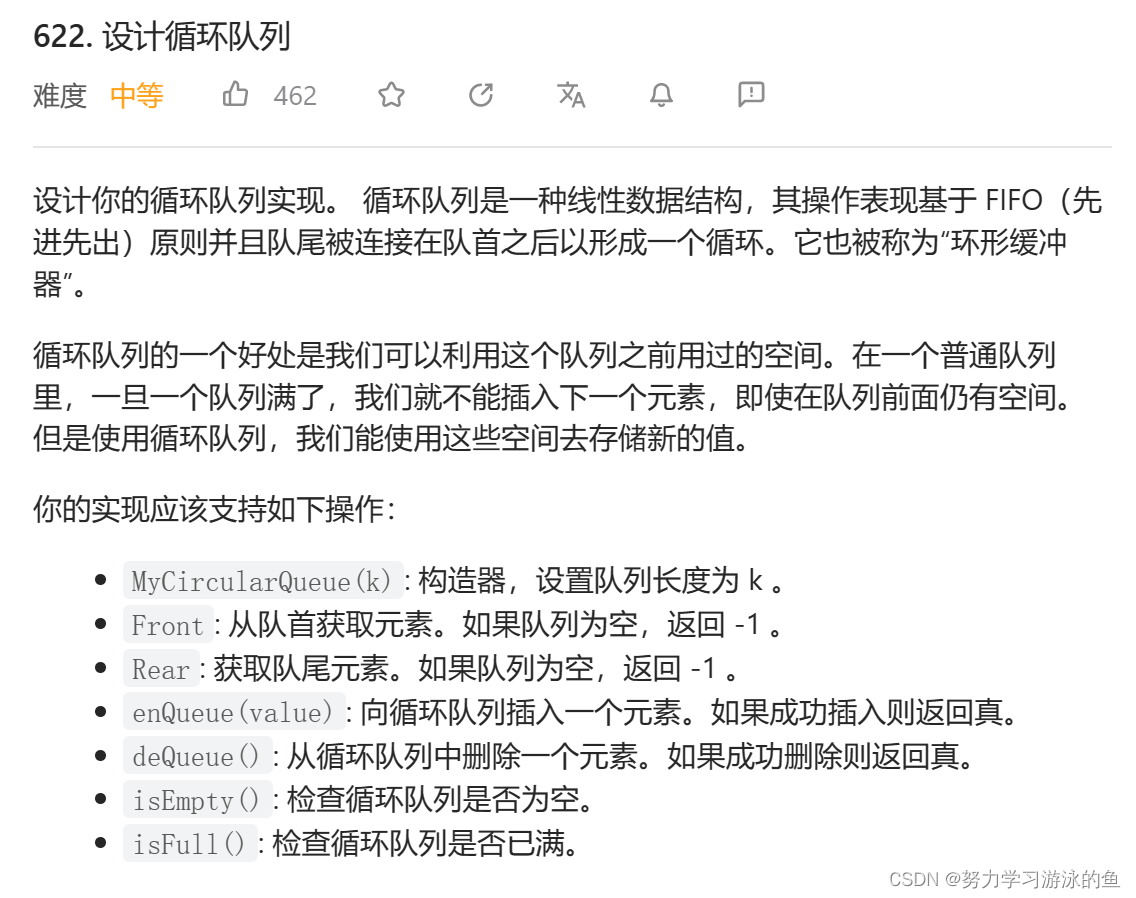
以下是示例：

以下是提示：

如何设计一个循环队列呢？这里我用数组来实现。结构的定义如下：

typedef struct {
    int* a;    // 存储数据的数组
    int k;     // 最多存储的有效数据个数
    int front; // 队头
    int rear;  // 队尾
} MyCircularQueue;

接下来分析如何入队列、出队列、判空、判满、取队头和队尾的数据。在不考虑越界的情况下，大概的逻辑是：

1. 数组初始化的空间能够存储k+1个数据。
2. 入队列时，我们在rear的位置插入数据，接着rear加1，所以rear标识的是最后一个数据的下一个位置。
3. 出队列时，我们让front加1即可。
4. 若front和rear相等，则队列为空。
5. 若rear加1后和front相等（front是rear的下一个），则队列为空。
6. 队头数据是下标为front的数据。
7. 队尾数据是下标为rear-1的数据。

但以上说法是有瑕疵的，因为加1后有可能向后越界，减1后有可能向前越界，这就需要进行特殊的处理，体现循环队列的特色：首尾相接，当向后越界时，会重新回到0；向前越界时，会来到数组的最后。具体的操作可以使用判断语句，比如当下标超出数组长度时，把下标置成0，不过我更喜欢使用取模的方式，这点后面会讲解。

初始化时，数组a的大小应该能够存储k+1个数据，也就是说，其中一个位置会空出来。为什么要这样处理呢？因为若数组只能容纳k个数据，判空和判满的条件就都是rear+1 == front，就无法区分空和满了。

MyCircularQueue* myCircularQueueCreate(int k) {
    // 开空间
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    // 数组开k+1个空间
    obj->a = (int*)malloc(sizeof(int) * (k + 1));
    // 初始化
    obj->k = k;
    obj->front = 0;
    obj->rear = 0;

    return obj;
}

入队列时，先要判断是否已满，满了就不能继续入队列了。接着插入数据，在rear的位置插入数据value，然后更新队尾rear。注意：不能简单的更新为rear+1，因为有可能越界，所以还要mod数组的长度，即(rear+1)%(k+1)。取模的效果是：当rear和k+1相等时，已经越界了，就会绕回去，重新变成0。后面的函数中，取模的效果是类似的。

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    // 满了就不能入队列
    if (myCircularQueueIsFull(obj))
        return false;

    // 插入数据
    obj->a[obj->rear] = value;
    // 更新队尾 = (旧队尾+1) % 容量
    obj->rear = (obj->rear + 1) % (obj->k + 1);
    return true;
}

出队列时，应该先判断是否为空，若空了就不能出队列了。接着，让队头front加1，但是和前面类似，还要mod数组的长度，防止越界。

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    // 空了就不能出队列
    if (myCircularQueueIsEmpty(obj))
        return false;

    // 更新队头 = (旧队头+1) % 容量
    obj->front = (obj->front + 1) % (obj->k + 1);
    return true;
}

取队头数据时，应该先判断是否为空，若未空则不能取队头数据。返回队头数据时，由于front就是队头，直接返回即可。

int myCircularQueueFront(MyCircularQueue* obj) {
    // 空了就返回-1
    if (myCircularQueueIsEmpty(obj))
        return -1;

    // 返回队头元素
    return obj->a[obj->front];
}

取队尾数据就有讲究了。首先判空，不必多说。接着返回队尾数据，而tail标识队尾数据的下一个位置，所以应返回rear-1位置的数据。但是减1后有可能变成负数，所以还要加上数组长度再取模，最终的下标是(rear-1 + k+1) % (k+1)。为什么不能直接取模呢？因为当对一个负数取模时，效果并不是我们想要的，我们应该尽量避免对负数取模。

int myCircularQueueRear(MyCircularQueue* obj) {
    // 空了就返回-1
    if (myCircularQueueIsEmpty(obj))
        return -1;

    // 返回队尾元素，下标为：(队尾-1+容量) % 容量
    //return obj->a[(obj->rear - 1 + obj->k + 1) % (obj->k + 1)];
    return obj->a[(obj->rear + obj->k) % (obj->k + 1)];
}

若front==rear，则队列为空。

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    // 队尾 == 队头
    return obj->rear == obj->front;
}

若rear+1 == front，则队列已满。但是直接这么判断是不对的，因为rear加1后有可能越界，所以要mod数组的长度再判断。

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    // (队尾+1) % 容量 == 队头
    return (obj->rear + 1) % (obj->k + 1) == obj->front;
}

销毁队列，只需销毁结构体中的成员，再销毁结构体即可。

void myCircularQueueFree(MyCircularQueue* obj) {
    // 释放空间
    free(obj->a);
    obj->a = NULL;
    obj->k = 0;
    obj->front = 0;
    obj->rear = 0;
    free(obj);
    obj = NULL;
}

完整的代码如下：

typedef struct {
    int* a;    // 存储数据的数组
    int k;     // 最多存储的有效数据个数
    int front; // 队头
    int rear;  // 队尾
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    // 开空间
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    // 数组开k+1个空间
    obj->a = (int*)malloc(sizeof(int) * (k + 1));
    // 初始化
    obj->k = k;
    obj->front = 0;
    obj->rear = 0;

    return obj;
}

bool myCircularQueueIsFull(MyCircularQueue* obj);

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    // 满了就不能入队列
    if (myCircularQueueIsFull(obj))
        return false;

    // 插入数据
    obj->a[obj->rear] = value;
    // 更新队尾 = (旧队尾+1) % 容量
    obj->rear = (obj->rear + 1) % (obj->k + 1);
    return true;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj);

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    // 空了就不能出队列
    if (myCircularQueueIsEmpty(obj))
        return false;

    // 更新队头 = (旧队头+1) % 容量
    obj->front = (obj->front + 1) % (obj->k + 1);
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    // 空了就返回-1
    if (myCircularQueueIsEmpty(obj))
        return -1;

    // 返回队头元素
    return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    // 空了就返回-1
    if (myCircularQueueIsEmpty(obj))
        return -1;

    // 返回队尾元素，下标为：(队尾-1+容量) % 容量
    //return obj->a[(obj->rear - 1 + obj->k + 1) % (obj->k + 1)];
    return obj->a[(obj->rear + obj->k) % (obj->k + 1)];
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    // 队尾 == 队头
    return obj->rear == obj->front;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    // (队尾+1) % 容量 == 队头
    return (obj->rear + 1) % (obj->k + 1) == obj->front;
}

void myCircularQueueFree(MyCircularQueue* obj) {
    // 释放空间
    free(obj->a);
    obj->a = NULL;
    obj->k = 0;
    obj->front = 0;
    obj->rear = 0;
    free(obj);
    obj = NULL;
}

轻松通过。

总结

循环队列的下标操作需要小心越界，若有可能越界，则要采取下面的处理：

1. 若下标大于数组范围，则要mod数组长度。
2. 若下标小于0，则要先加数组长度，再mod数组长度。

感谢大家的阅读！