您现在的位置是:首页 >技术交流 >八大排序-直接插入排序、希尔排序、直接选择排序、冒泡排序、堆排序、快速排序、归并排序、基数排序网站首页技术交流
八大排序-直接插入排序、希尔排序、直接选择排序、冒泡排序、堆排序、快速排序、归并排序、基数排序
目录
如果本篇博客对您有一定的帮助,请您留下宝贵的三连:留言+点赞+收藏哦。
前言
在计算机科学领域中,排序算法是最基础和最重要的算法之一。
排序算法可以将一个无序的数据序列按照一定的规则进行排序,使得数据更加有序,方便后续的数据处理。常见的排序算法有八大经典算法:冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序和基数排序。每个算法都有其独特的思想和性能特点。对于一个合适的排序算法来说,它既要保证排序的正确性,又要具备高效的时间和空间复杂度。
本文将分别介绍八大排序算法的原理、实现和优缺点。对于有一定算法基础的读者,本文也提供了几种算法的优化方法,可以帮助他们更好地应用这些排序算法。
直接插入排序(Insertion Sort)
一、概念及其介绍
插入排序(InsertionSort),一般也被称为直接插入排序。
对于少量元素的排序,它是一个有效的算法。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增 1 的有序表。
在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
二、过程图示
假设前面 n-1(其中 n>=2)个数已经是排好顺序的,现将第 n 个数插到前面已经排好的序列中,然后找到合适自己的位置,使得插入第n个数的这个序列也是排好顺序的。
按照此法对所有元素进行插入,直到整个序列排为有序的过程,称为插入排序。
从小到大的插入排序整个过程如图示:
第一轮:从第二位置的 6 开始比较,比前面 7 小,交换位置。
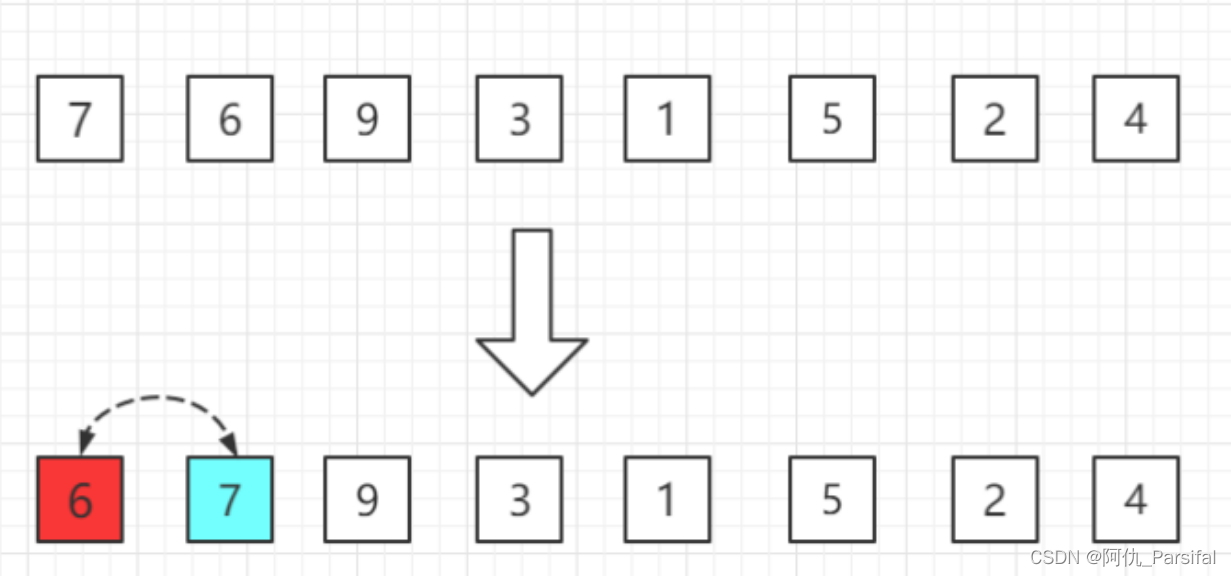
第二轮:第三位置的 9 比前一位置的 7 大,无需交换位置。

第三轮:第四位置的 3 比前一位置的 9 小交换位置,依次往前比较。
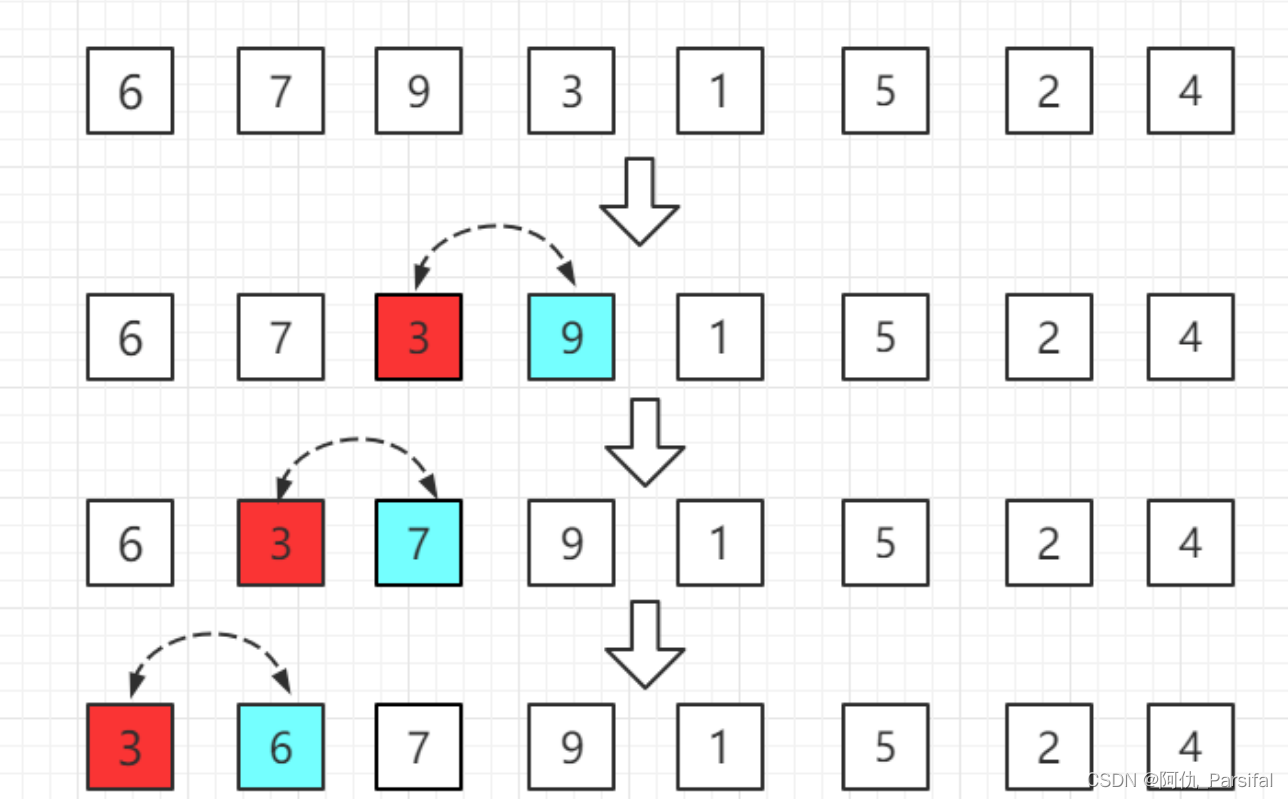
第四轮:第五位置的 1 比前一位置的 9 小,交换位置,再依次往前比较。
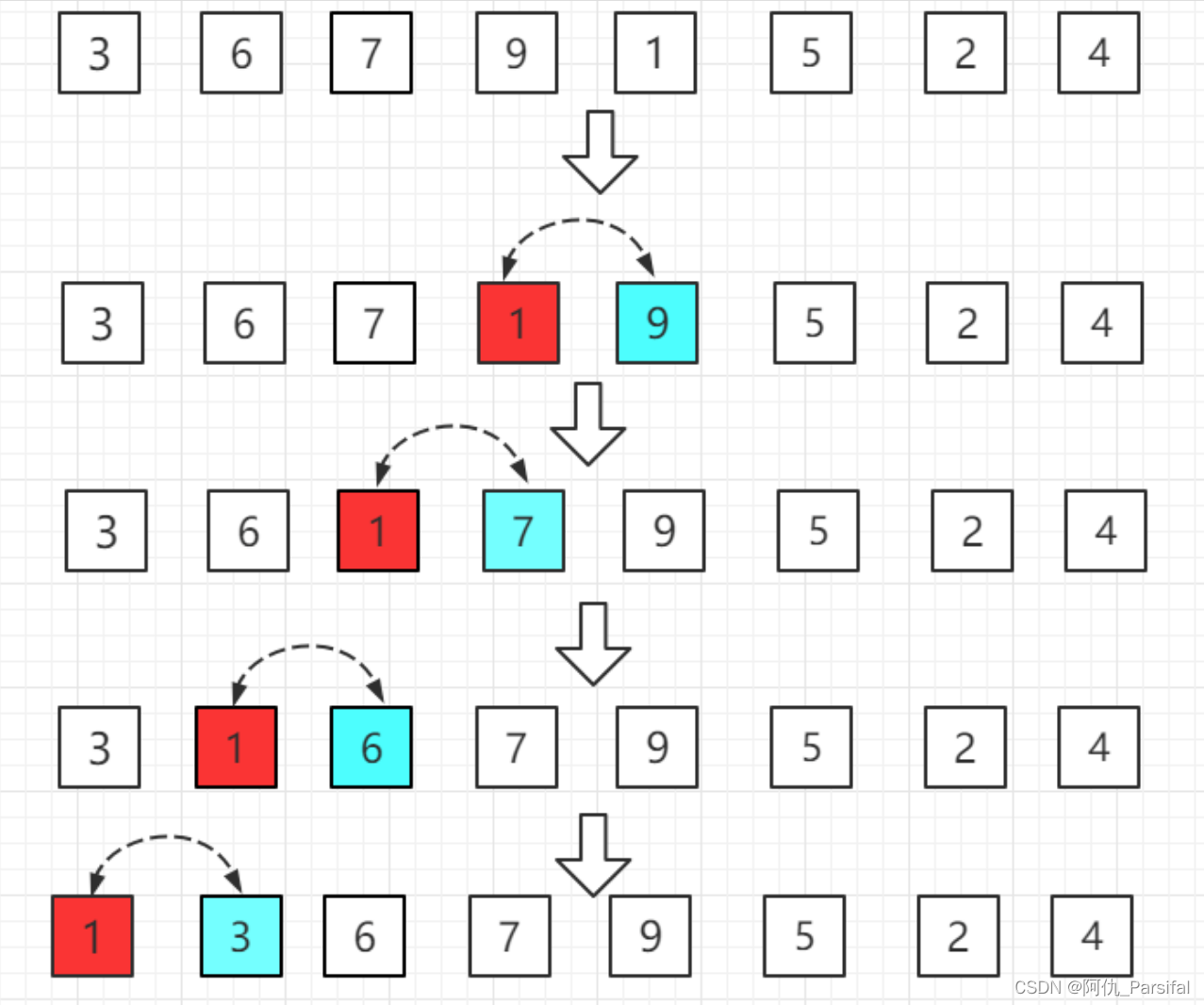
三、代码
对[1,9,6,5,7,6,8,2,4]进行直接排序
public static void sort(int[] a) {
for (int i = 1; i < a.length; i++) { //a[0]不用排序
int temp = a[i]; //记录待排序元素的值
for (int j = i - 1; j >=0; j--) {
if (temp < a[j]) {
a[j + 1] = a[j];
} else {
break;
}
a[j] = temp;
}
System.out.println("第" + i + "轮排序的结果为" + Arrays.toString(a));
}
}
public class InsertSort {
//核心代码---开始
public static void sort(Comparable[] arr){
int n = arr.length;
for (int i = 0; i < n; i++) {
// 寻找元素 arr[i] 合适的插入位置
for( int j = i ; j > 0 ; j -- )
if( arr[j].compareTo( arr[j-1] ) < 0 )
swap( arr, j , j-1 );
else
break;
}
}
//核心代码---结束
private static void swap(Object[] arr, int i, int j) {
Object t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
public static void main(String[] args) {
Integer[] arr = {1,9,6,5,7,6,8,2,4};
sort(arr);
for( int i = 0 ; i < arr.length ; i ++ ){
System.out.print(arr[i]);
System.out.print(' ');
}
}
}四、复杂度
时间复杂度也是 O(n^2),空间复杂度为常数阶 O(1)
希尔排序(Shell Sort)
一、概念
希尔排序(Shell's Sort)是插入排序的一种,是插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。
二、实现思路
- 先分组:找到一个间隔,每隔一定的间隔把这些元素排成一组(在希尔排序当中对间隔没有明确的要求,可以任意找间隔,通常会取总长度的一半)
- 对组内元素进行插入排序
- 重新设置间隔、分组,在原来的间隔基础之上减半
- 组内元素排序
- 直到间隔为1,间隔为1以为着所有的元素为一组,此时进行最后一次组内排序
三、图示过程
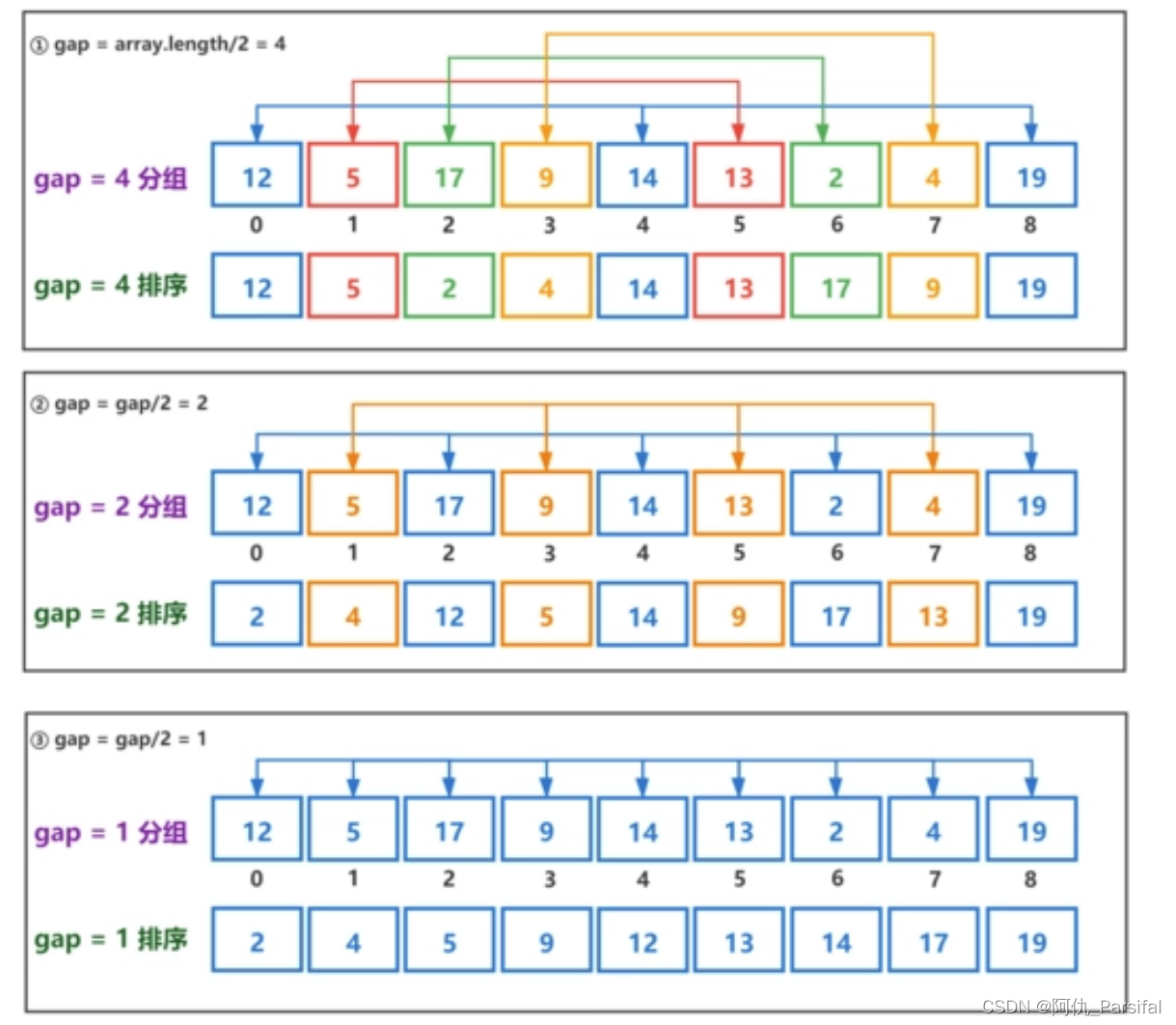
四、代码
4.1代码
public class ShellSort {
public static void main(String[] args) {
int[] arr = { 8, 9, 1, 7, 2, 3, 5, 4, 6, 0 };
System.out.println("排序前的数组为:" + Arrays.toString(arr));
shellSort(arr);
System.out.println("排序后的数组为:" + Arrays.toString(arr));
}
public static void shellSort(int[] arr) {
int n = arr.length;
// 初始步长,可以根据实际情况调整
int gap = n / 2;
while (gap > 0) {
// 从数组第gap个元素开始,逐个对其所在组进行直接插入排序操作
for (int i = gap; i < n; i++) {
int j = i;
int temp = arr[j];
if (arr[j] < arr[j - gap]) {
while (j - gap >= 0 && arr[j - gap] > temp) {
// 插入排序采用交换法
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = temp;
}
}
// 得到新的步长
gap = gap / 2;
}
}
}4.2运行结果
排序前的数组为:[8, 9, 1, 7, 2, 3, 5, 4, 6, 0]
排序后的数组为:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
4.3解释
希尔排序是插入排序的一种改进,其核心思想是将原序列分成若干个子序列,对每个子序列进行插入排序,随着排序过程的进行,逐渐缩小子序列的长度,直到整个序列变为有序。希尔排序的关键在于步长的选择,不同的步长序列会影响排序的效率。
在上面的代码中,我们采用的是初始步长为数组长度的一半,然后不断将步长除以2,直到步长为1时结束排序。在每个步长下,我们将数组分成若干个子序列,对每个子序列进行插入排序。具体来说,我们从第gap个元素开始,逐个对其所在组进行插入排序操作。在插入排序过程中,我们采用交换法,即将当前元素与其前面的元素进行比较,如果前面的元素比当前元素大,则将前面的元素后移,直到当前元素找到合适的位置插入。
最终,当步长为1时,整个序列就变成了有序序列,排序结束。希尔排序的时间复杂度与步长序列的选择有关,最坏情况下为O(n^2),但是在大部分情况下,其时间复杂度都能达到O(nlogn)的级别,比插入排序要快很多。
五、复杂度
不稳定,时间复杂度是O(nlogn)~O(n^2),空间复杂度是O(1)
堆排序(Heap Sort)
一、概念
1.1什么是堆
- 分为大顶堆和小顶堆
- 符合完全二叉树
- 父节点大于(或小于)子节点
- 第一个非叶子节点:n/2-1(向下取整)
二、排序思想
- 首先将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是堆结构的顶端
- 将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1
- 将剩余的n-1个数再构造成大根堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组
三、图示过程
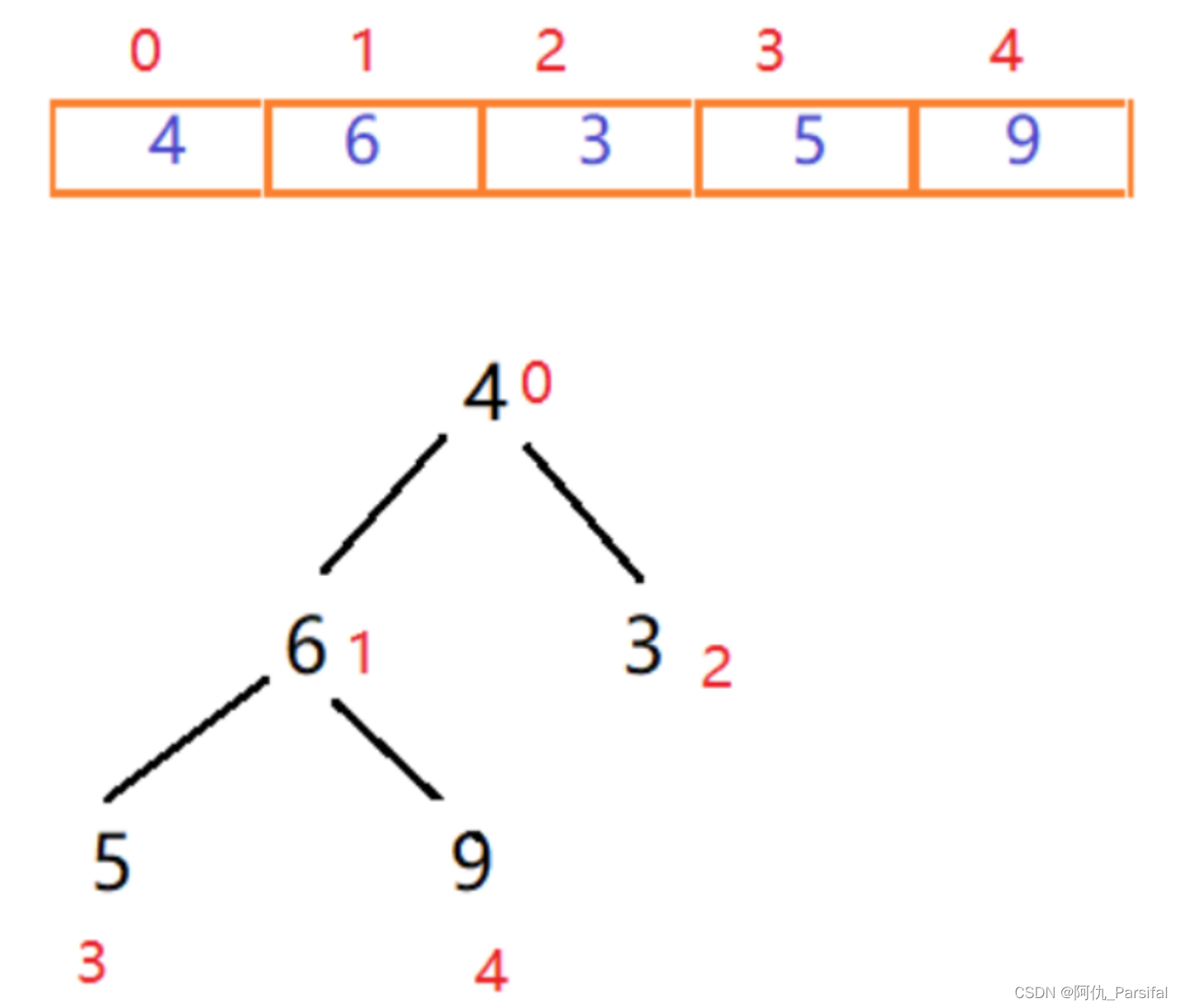
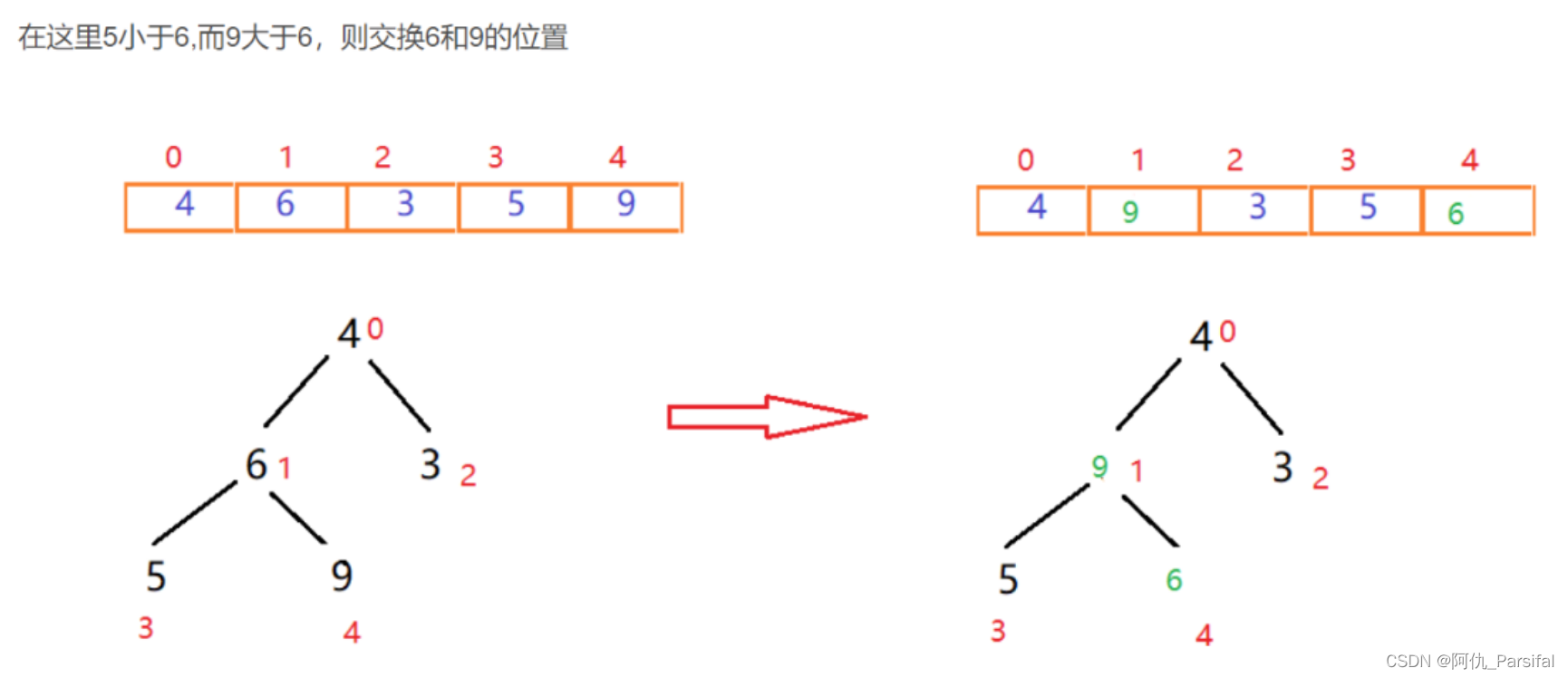
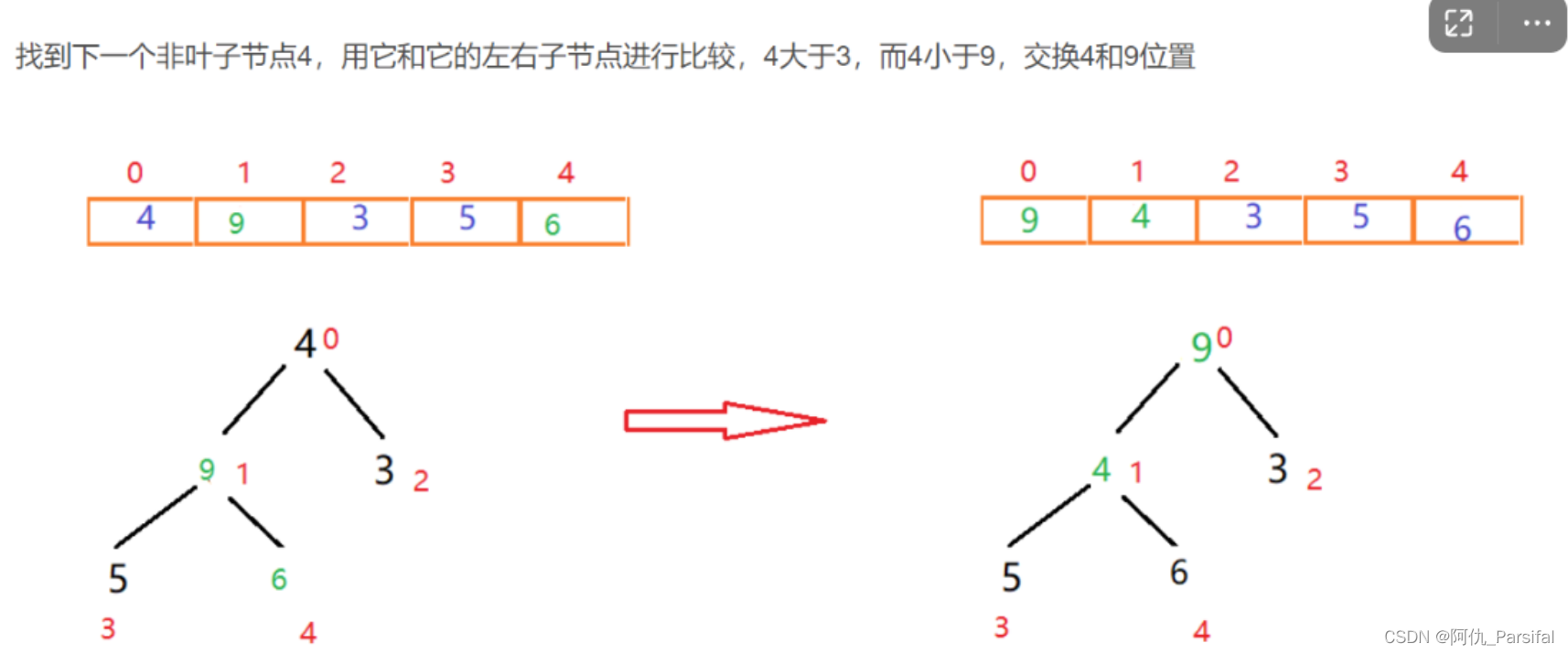
最大值和末尾的最小值交换位置
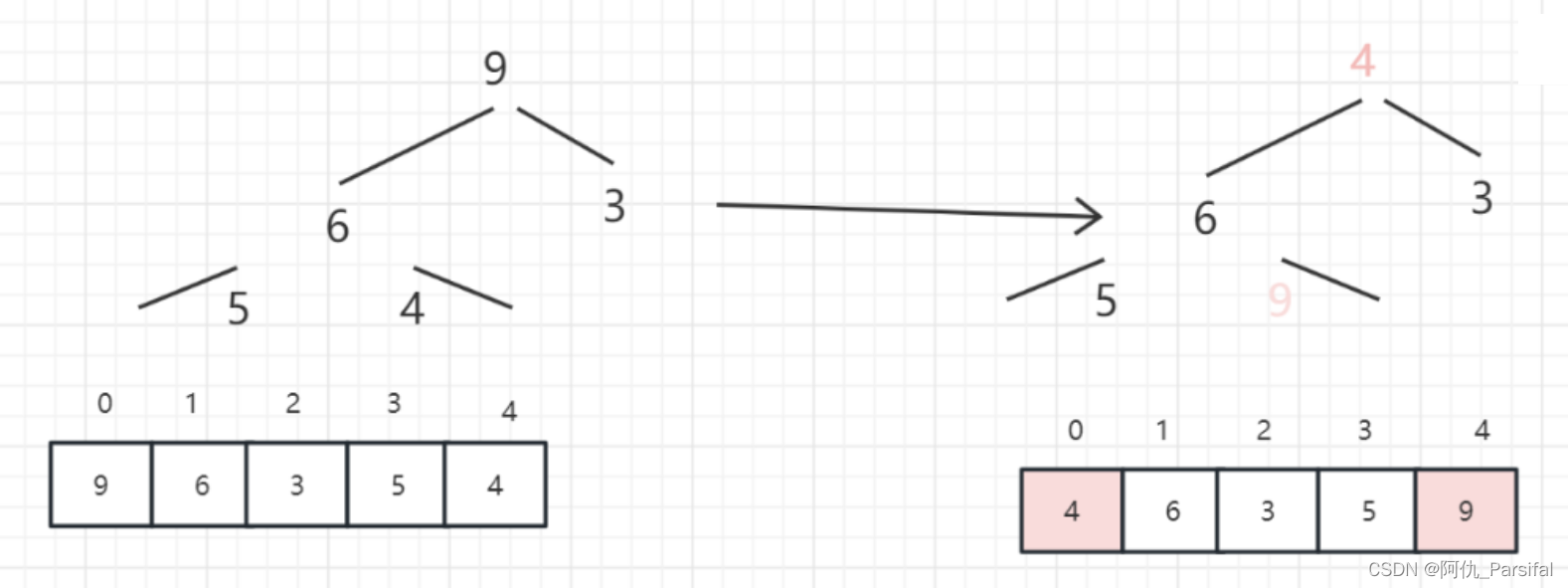
重复以上操作
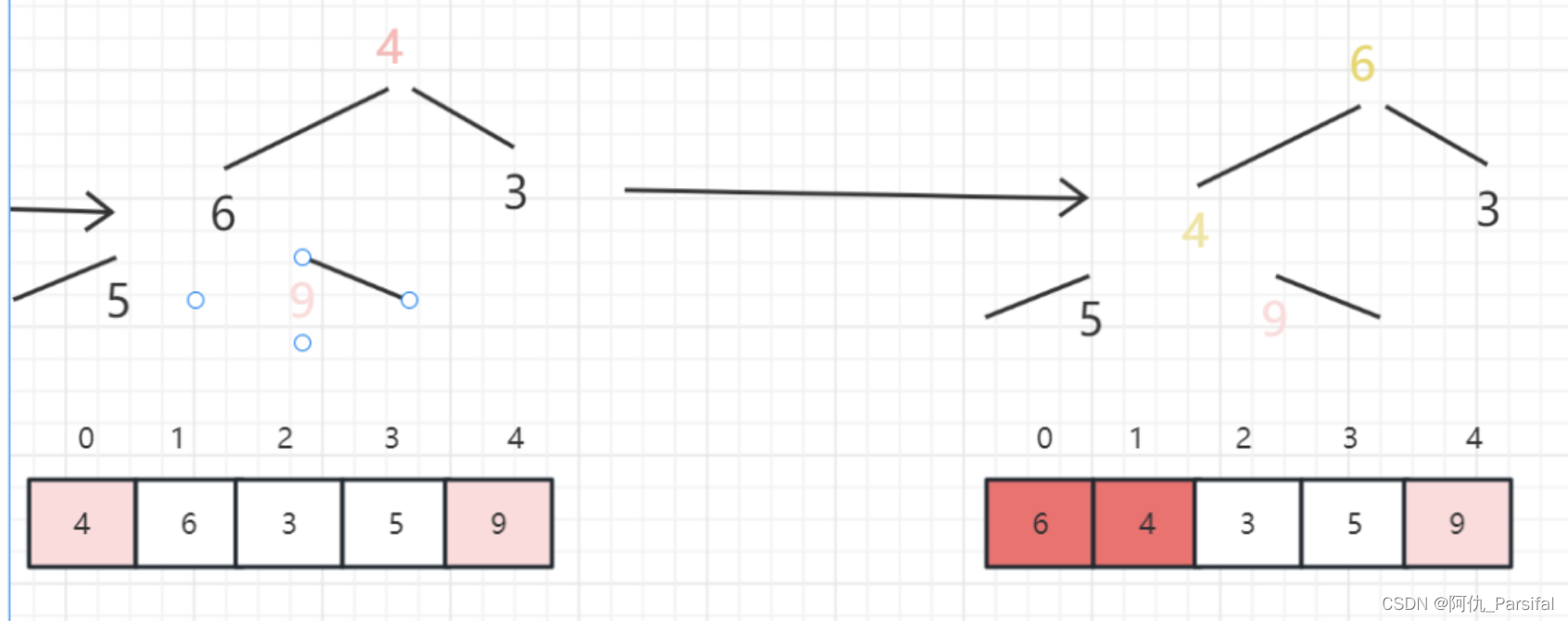
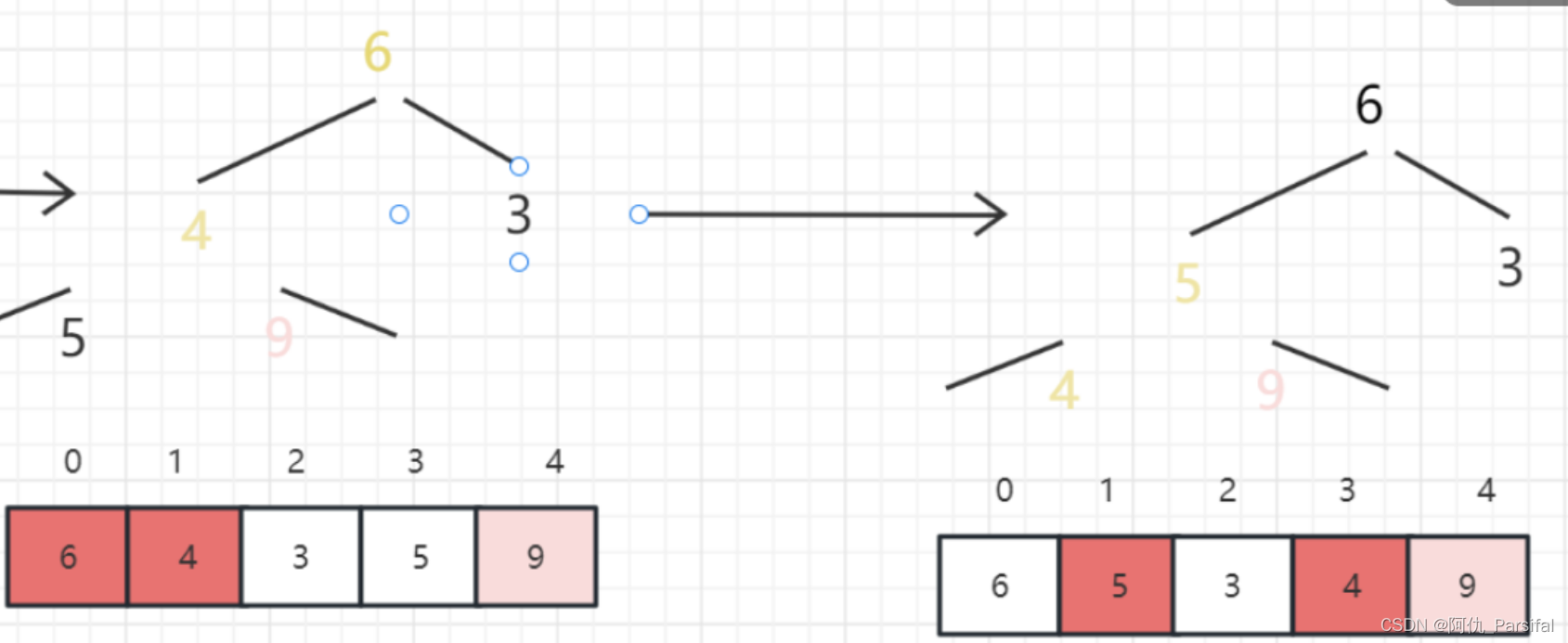
四、代码
4.1代码
public class HeapSort {
public static void heapSort(int[] arr) {
// 构建初始大根堆
buildMaxHeap(arr);
// 从最后一个非叶子节点开始,依次向上调整堆
for (int i = arr.length - 1; i > 0; i--) {
swap(arr, 0, i); // 将堆顶元素(最大值)与最后一个元素交换
maxHeapify(arr, 0, i); // 调整堆
}
}
private static void buildMaxHeap(int[] arr) {
// 从最后一个非叶子节点开始,依次向上调整堆
for (int i = arr.length / 2 - 1; i >= 0; i--) {
maxHeapify(arr, i, arr.length);
}
}
private static void maxHeapify(int[] arr, int i, int heapSize) {
int left = 2 * i + 1; // 左子节点下标
int right = 2 * i + 2; // 右子节点下标
int largest = i; // 最大值下标
// 找到左、右子节点中的最大值
if (left < heapSize && arr[left] > arr[largest]) {
largest = left;
}
if (right < heapSize && arr[right] > arr[largest]) {
largest = right;
}
// 如果最大值不是当前节点,交换最大值和当前节点,继续向下调整
if (largest != i) {
swap(arr, i, largest);
maxHeapify(arr, largest, heapSize);
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) {
int[] arr = {5, 2, 6, 0, 3, 9, 1, 7, 4, 8};
heapSort(arr);
for (int i : arr) {
System.out.print(i + " ");
}
}
}4.2运行结果
排序前的数组为:[5, 2, 6, 0, 3, 9, 1, 7, 4, 8]
排序后的数组为:[0, 1 ,2 ,3 ,4 ,5 ,6 ,7 ,8, 9]
4.3解释
代码中的buildMaxHeap()方法用于构建初始大根堆,maxHeapify()方法用于调整堆,heapSort()方法实现了堆排序算法。main()方法中用一个示例数组进行测试,并输出排序结果
直接选择排序(Selection Sort)
一、概念
- 选择排序是一种简单直观的排序算法
- 无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候,数据规模越小越好。
- 唯一的好处可能就是不占用额外的内存空间
二、实现思路
- 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
- 再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
- 重复第二步,直到所有元素均排序完毕。
三、图示过程
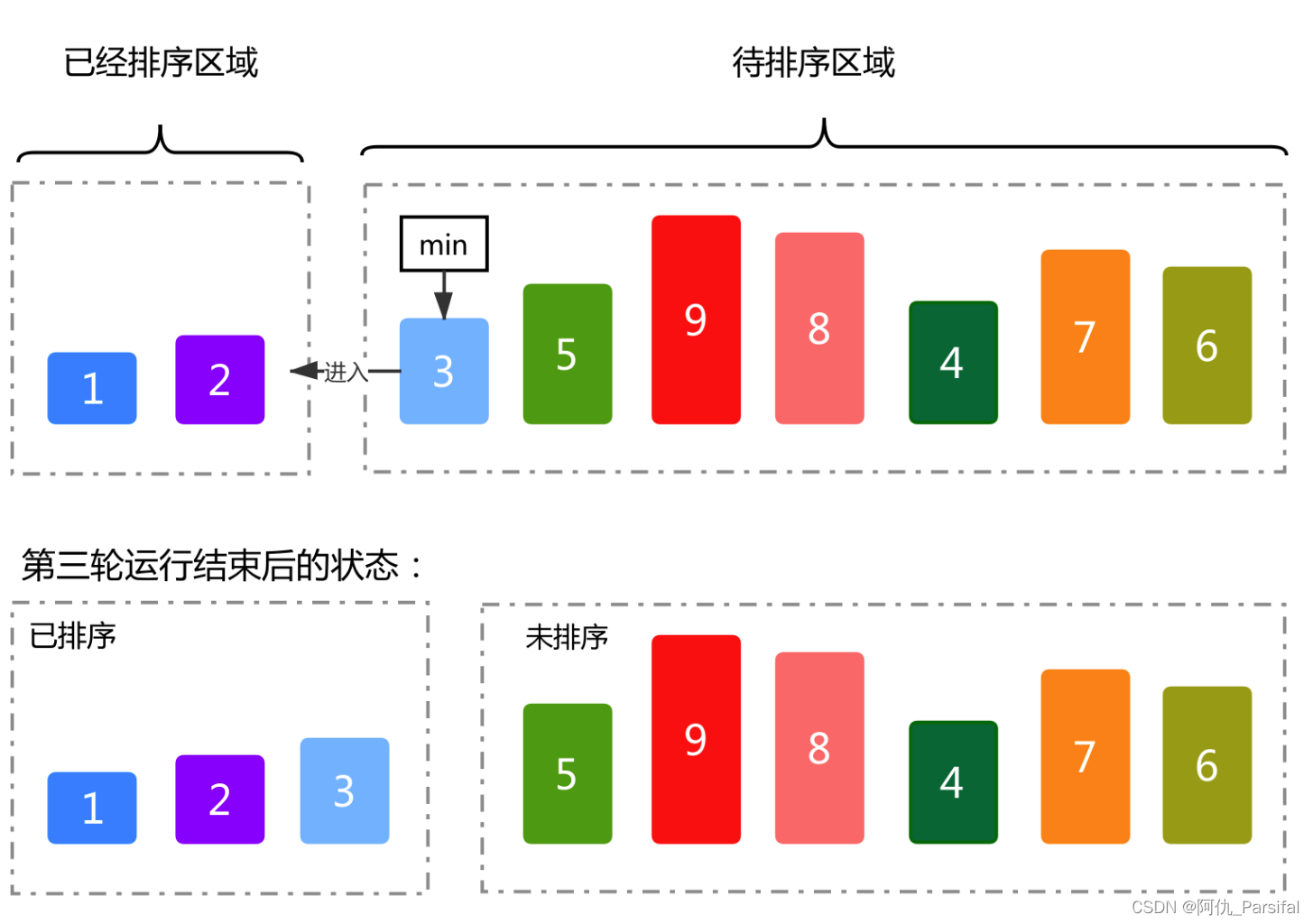
四、代码
4.1代码
//Selection Sort选择排序
public class Selection {
public static void main(String[] args) {
int[] arr = {23,34,21,243,67,432,23,34};
System.out.println(Arrays.toString(selection(arr)));
}
//选择排序
public static int[] selection(int[] arr) {
int temp = 0; //定义数据交换时的第三方变量
for (int i = 0; i < arr.length - 1; i++) {
int min = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[min] > arr[j]) { //如果arr[j]的值小于arr[min]
min = j; //保存j的索引
}
}
temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
System.out.println("第" + (i + 1) + "轮插入" + Arrays.toString(arr));
}
return arr;
}
}
4.2运行结果
排序前的数组为:[23,34,21,243,67,432,23,34]
排序后的数组为:[21,23,23,34,34,67,243,432]
五、代码优化
5.1代码方案一
第一种:使用一个if判断 i == arr.length-2 ,直接去掉最后一轮对比
问题,如果倒数第二轮排序 最后一位元素比倒数第二位元素小,那么去掉最后一轮排序,最终结果是没有排序完成的
//Selection Sort选择排序
public class Selection {
public static void main(String[] args) {
int[] arr = {23,34,21,243,67,432,23,34};
System.out.println(Arrays.toString(selection(arr)));
}
//选择排序
public static int[] selection(int[] arr) {
int temp = 0; //定义数据交换时的第三方变量
for (int i = 0; i < arr.length - 1; i++) {
if( i == arr.length-2){ //如果i=数组的最后两个值
break; //退出循环
}
int min = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[min] > arr[j]) { //如果arr[j]的值小于arr[min]
min = j; //保存j的索引
}
}
temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
System.out.println("第" + (i + 1) + "轮插入" + Arrays.toString(arr));
}
return arr;
}
}
5.2代码方案二
第二种优化:
if(i != min ) { //判断只有在min=i时才会运行下面的代码
这种优化方法省略了很多不必要的代码运行,并优化最后一轮是否需要对比
//Selection Sort选择排序
public class Selection {
public static void main(String[] args) {
int[] arr = {23,34,21,243,67,432,23,34};
System.out.println(Arrays.toString(selection(arr)));
}
//选择排序
public static int[] selection(int[] arr) {
int temp = 0; //定义数据交换时的第三方变量
for (int i = 0; i < arr.length - 1; i++) {
int min = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[min] > arr[j]) { //如果arr[j]的值小于arr[min]
min = j; //保存j的索引
}
}
if(i != min ) { //判断只有在min=i时才会运行下面的代码
temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
System.out.println("第" + (i + 1) + "轮插入" + Arrays.toString(arr));
}
}
return arr;
}
}
六、复杂度
是一种不稳定排序,时间复杂度是O(n^2),空间复杂度是O(1)
结构化:各个排序对比表格
| 排序算法 | 分类 | 规则 | 稳定性 | 时间复杂度 | 空间复杂度 | 优点 | 缺点 |
|---|---|---|---|---|---|---|---|
| 插入排序(Insertion Sort) | 插入排序 | 将元素插入到有序序列中 | 稳定 | O(n^2) | O(1) | 对小规模数据排序效率高 | 大规模数据效率低 |
| 希尔排序(Shell Sort) | 插入排序的升级版,先进行分组插入排序 | 不稳定 | O(nlogn)~O(n^2) | O(1) | 对大规模数据排序效率高 | 步长选择不当时效率低 | |
| 冒泡排序(Bubble Sort) | 交换排序 | 相邻元素比较 | 稳定 | O(n^2) | O(1) | 实现简单,空间复杂度低 | 大规模数据效率低, 时间复杂度高 |
| 选择排序(Selection Sort) | 找到最小/大元素 | 不稳定 | O(n^2) | O(1) | 简单,不占用额外空间 | 时间复杂度高 | |
| 归并排序(Merge Sort) | 分治思想,将序列不断拆分成子序列再合并 | 稳定 | O(nlogn) | O(n) | 对大规模数据排序效率高 | 占用额外空间 | |
| 快速排序(Quick Sort) | 分治思想,选取一个基准值进行比较交换 | 不稳定 | O(nlogn)~O(n^2) | O(logn)~O(n) | 对大规模数据排序效率高 | 最坏时间复杂度较高 | |
| 堆排序(Heap Sort) | 将元素构建成最大/小堆,每次取堆顶元素 | 不稳定 | O(nlogn) | O(1) | 对大规模数据排序效率高 | 空间复杂度高 | |
| 基数排序(Radix Sort) | 将元素按位数进行排序 | 稳定 | O(d(n+k)) | O(n+k) | 适用于对多关键字排序 | 数据集分布不均匀时效率低 |






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结