DeepGPS: Deep Learning Enhanced GPS Positioning in Urban Canyons

IEEE TMC｜深度学习增强的城市峡谷GPS定位
https://github.com/bducgroup/DeepGPS

Abstract

全球定位系统（GPS）在我们的日常生活中为许多新的应用带来了好处，例如导航、拼车和基于位置的服务。尽管GPS在大多数地方都能很好地工作，但由于非直瞄卫星的信号反射，它在城市峡谷中的性能是众所周知的差。人们已经做出了巨大的努力来减轻非直瞄信号的影响，而之前的工作在很大程度上依赖于精确的专有3D城市模型或其他第三方资源，这些资源不容易获得。

在本文中，我们介绍了DeepGPS，这是一种深度学习增强型GPS定位系统，它可以只考虑一些简单的上下文信息来校正GPS估计。DeepGPS融合了环境因素，包括GPS初始位置周围的建筑高度和道路分布，以及卫星状态来描述定位上下文，并利用编码器-解码器网络模型从大量标记的GPS样本中隐式学习定位上下文和GPS估计之间的复杂关系。因此，在给定定位上下文的情况下，模型可以准确地预测每个错误GPS估计的正确位置。我们用一个新的约束掩码进一步改进了模型，以过滤掉无效的候选位置，并用一个简单的迁移模型实现连续定位。

使用大型公交车轨迹数据集和现场GPS测量，实现了原型系统并对其进行了实验评估。实验结果表明，DeepGPS显著提高了城市峡谷中的GPS性能，例如，平均有效校正了90.1%的GPS估计，精度提高了64.6%。

1 INTRODUCTION

全球导航卫星系统（GNSS），如众所周知的全球定位系统（GPS），已使许多智能应用受益，包括导航[65]、即时配送[69]、拼车[40]、自动驾驶[12]和基于位置的服务[34]。精确定位对于这些应用程序提供有效和高效的服务至关重要。虽然GPS在大多数地方通常工作良好，但在城市峡谷中，GPS误差可能大于50米[28]。

由于高层建筑对卫星信号的反射[33]，城市峡谷中的GPS误差主要来自多径干扰或非视距（Non-Line of Sight NLOS）接收的影响。尽管一些硬件或软件设计[18]、[27]、[44]可以很好地解决多径干扰问题，但GPS接收器处的非视距卫星信号仍然是城市峡谷中定位误差的主要来源。原则上，GPS接收器需要从至少四颗卫星接收信号，以准确地对其位置进行三角测量[33]。在城市峡谷场景中，非视距卫星的信号可能会被一座甚至多座高层建筑反射，并导致所谓的伪距（目标卫星和GPS接收器之间距离的近似值）更大，从而导致定位误差。

早期工作为了减轻非视距接受的影响，做出的努力：早期的工作[21]对卫星信号应用射线跟踪算法来计算伪距误差，伪距误差必须使用专用硬件重建街道建筑物的反射表面，例如全景相机[54]和激光雷达[57]。基于专有的3D城市模型，最近的大多数工作都利用建筑几何形状来计算GPS初始位置周围的候选位置和接收器观测值之间的信号路径[29]、[39]、[45]、[48]或卫星能见度[23]、[49]、[60]、[63]、[68]的相似性，并输出具有最佳匹配的点作为解决方案。然而，这些作品在很大程度上依赖于精确的专有3D城市模型或其他第三方资源，例如全景图像[39]，这些资源不容易访问，因此在很大程度上将限制其实际应用。

尽管之前的工作有局限性，但它们提示我们：应该存在一些映射函数f，可以将GPS估计及其周围环境映射到接收器实际所在的地面实况位置。一方面，对于由一对经纬度表示的给定位置，其周边环境因素对卫星信号的影响是长期一致的。另一方面，GPS卫星按一定周期有规律地运行，因此它们的位置是可以预测的。当然，由于巨大的计算和存储成本，不可能枚举所有定位上下文来找到映射函数f，而我们可以通过利用深度学习的强大表示能力，建立一个深度神经网络来近似映射函数f来增强城市峡谷中的GPS定位[35]。GPS轨迹[70]为学习给定区域的深度神经网络模型提供了丰富的训练数据。经过良好训练的模型可以为该地区的用户提供快速准确的GPS定位。

在本文中，我们提出了一种深度学习增强型GPS定位系统DeepGPS，它可以在城市峡谷中实现精确定位。我们建立了一个深度神经网络，从大量标记的GPS样本中隐式地捕捉定位上下文和地面实况位置之间的复杂关系。训练后的模型作为黑盒，可以有效地将错误的GPS估计转换为正确的位置，从而大大提高城市峡谷中的定位精度。

然而，实例化DeepGPS需要解决三个关键挑战。

1. 首先，有多种因素（例如建筑物的布局和高度、卫星分布、人类动力学等）将影响城市峡谷中的GPS精度，而这些因素以不同的形式存在，导致它们具有不同的维度。如何正确地表示和融合相关的定位上下文作为深度神经网络的输入，同时又不会丢失信息，这是一个挑战。为了解决这个问题，我们将所有上下文因素转换为相同大小的矩阵，并将它们组合为一个整体的多源数据输入。这样的表示使我们能够利用计算机视觉[32]、[36]中基于2D图像的技术的最新进展，这些技术有助于捕捉GPS初始位置周围环境因素之间的空间相关性。

2. 其次，根据GPS估计和其他输入预测正确的位置可以建模为回归问题。由于位置通常表示为一对纬度和经度，因此由于浮点数的巨大搜索空间，很难训练回归模型。因此，如何对位置校正问题进行建模至关重要，因为它也决定了深度神经网络的架构。为了应对这一挑战，我们分析了城市峡谷中的GPS误差分布，并在GPS的初始位置周围生成了一组候选单元。然后，我们将位置校正问题转化为分类问题，目的是预测哪个单元最有可能包含地面实况位置。为了解决这个分类问题，我们采用了编码器-解码器网络。该模型由一个从输入矩阵中提取特征的编码器和两个解码器组成，即距离解码器和位置解码器，它们分别输入编码器生成的特征图以预测定位误差和校正位置。更重要的是，这两个解码器共享来自同一编码器的信息，并相互约束以预测最可能的误差和位置，这可以与观测结果最佳匹配。此外，我们将环境上下文嵌入到约束掩码中，该掩码可以通过过滤掉不可访问的单元来提高模型的准确性。

3. 第三，大多数基于位置的应用程序通常需要跟踪感兴趣的对象，这需要连续准确的定位。尽管我们可以利用该模型来分别校正每个GPS估计，但这种方法忽略了用户运动之间的时间相关性，因此效率低下。事实上，我们可以采用粒子滤波[59]等先进技术来跟踪用户的位置，然而，这些解决方案需要额外的设备来收集移动数据。因此，使模型很好地支持连续本地化仍然是一个挑战。为此，我们提出了一种简单的基于移动模型的连续定位方法。我们使用最新的固定位置来更新用户的移动模型，这有助于在给定两个定位实例之间的时间间隔的情况下计算用户的可达区域。可达区域对候选单元提供了不同的置信度，并帮助我们准确有效地确定具有正确位置的单元。

总之，本文做出了以下贡献：

• 据我们所知，我们是第一个通过学习不同定位环境和GPS估计之间的关系来提高城市峡谷中GPS性能的团队。
• 我们设计并实现了DeepGPS，它建立在编码器-解码器网络架构上，该系统可以准确预测定位错误，并从错误的GPS估计和多源数据中校正位置。
• 我们将领域知识纳入一个新的约束掩码中，该掩码进一步改进了神经网络，并提出了一个移动模型来实现连续定位。
• 开发了原型系统并对其进行了实验评估。基于大型公交车GPS轨迹数据集和现场GPS测量的广泛评估结果表明了DeepGPS的有效性。平均而言，我们的系统可以有效地校正90.1%的GPS估计，定位精度提高了64.6%。

本文的其余部分组织如下。我们在第2节中介绍了背景和动机。DeepGPS的设计分别在第3节和第4节中阐述和实施。性能评估在第5节中进行。我们在第6节中回顾了相关工作，并在第7节中介绍了讨论情况。最后，第8节对本文进行了总结。

2 BACKGROUND AND MOTIVATION

在这一部分中，我们将介绍GPS的背景，讨论GPS在城市峡谷中的表现，然后通过分析前人的工作来启发我们对DeepGPS的设计。

2.1 The Prime of GPS

GPS导航系统由三个部分组成：卫星星座、地面站和用户的GPS接收器。具体而言，卫星星座由32颗卫星组成，每颗卫星每12小时绕地球一周，并在地球上空连续广播其位置和其他元数据[33]。元数据包括每个卫星的各种属性，例如卫星的位置。地面站通过向所有卫星发送控制其轨道和轨迹的参数来监测和管理所有卫星。

此外，卫星携带稳定的原子钟，这些原子钟与地面站的时钟精确同步。GPS接收器从可用的卫星接收信号，并通过将光速与信号的传播延迟相乘来计算每个信号的传播距离，即伪距。根据观测卫星的位置及其伪距，接收机在如下约束条件下使用最小二乘法估计其位置$(x,y,z)$：
$$\sqrt{(x-x_i{)}^2+(y-y_i{)}^2+(z-z_i{)}^2}={\ell }_i$$
对于$i=1,2,\cdot \cdot \cdot ,m$，其中$m$是接收器的可见卫星数，$(x_i,y_i,z_i)$是第$i$颗卫星的位置，以及${\ell }_i$是接收器和第$i$颗卫星之间的测量距离。在实践中，接收器的时钟与卫星的时钟不同步，因此接收器必须至少有四颗卫星才能确定其位置以及接收器和卫星之间的未知时间偏差。

独立的GPS接收器会受到许多误差源的影响，这些误差源会严重影响GPS定位性能[33]。例如，大气条件的不一致会影响GPS信号的传播速度，导致电离层延迟和对流层延迟。此外，由于地球自转和卫星速度造成的多普勒效应也会影响GPS信号的传播时间，并引入定位误差。此外，直接从卫星接收相同信号并通过反射接收的多径干扰和仅通过反射接收信号的非视距卫星都将影响伪距离估计。最后，值得注意的是，尽管卫星时钟非常准确，但它们仍然不完美，每天的时钟误差约为8.64至17.28纳秒[3]。为了简单起见，我们只提到了GPS定位中的几个主要误差源，更多关于GPS误差的分析可以在[3]、[33]中找到。

存在各种技术，例如差分GPS[25]，以补偿现代GPS接收机中大气条件不一致和多普勒效应引起的误差[39]。与可以通过接收更多卫星信号来修复的GPS接收器时钟误差不同，可以使用拟合多项式模型来校正卫星时钟误差[52]。其他两个误差源，即多径干扰和非视距卫星，仍然是GPS定位的主要挑战，在城市峡谷中尤为严重[16]、[20]、[23]。

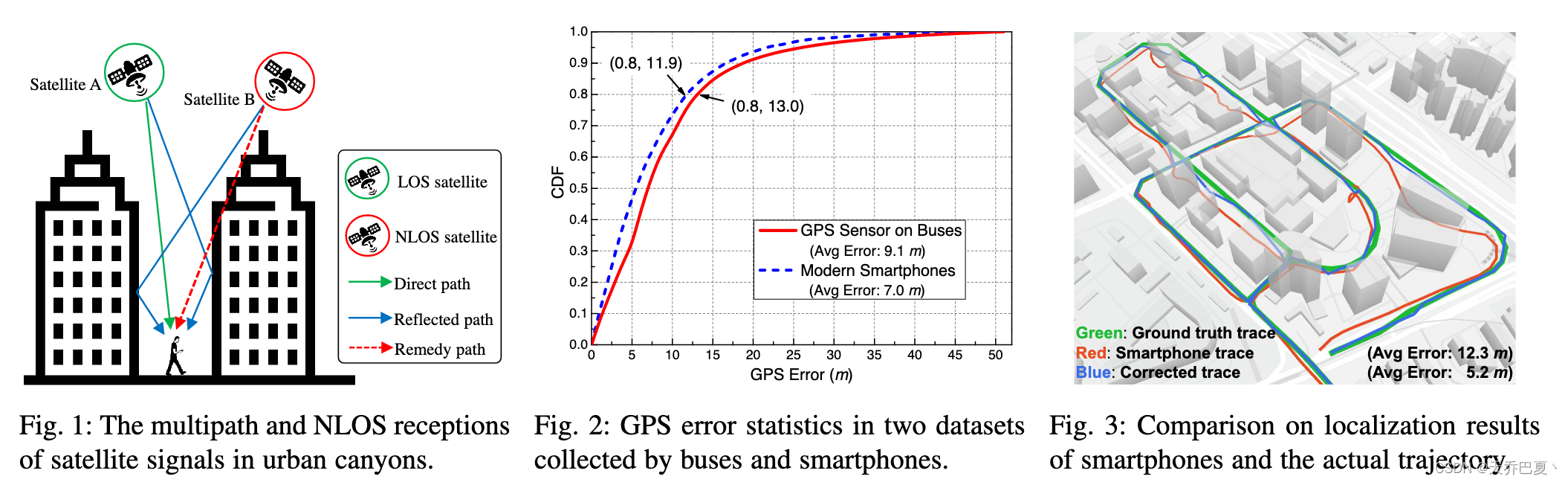
2.2 How GPS Performs in Urban Canyons

在城市峡谷中，卫星信号经常被密集分布的建筑物反射或阻挡。因此，GPS接收器无法接收到足够的读数或错误地估计伪距，从而导致更大的定位误差，例如超过50米[28]。如图1所示，用户的接收器从卫星a接收直接信号（即绿线）和反射信号（即蓝线）。这两个信号对接收器形成多径接收，并干扰其定位。由于卫星B被建筑物阻挡，接收器只能接收来自卫星B的反射信号，因此接收器称卫星B为非视距卫星。与直接信号相比，反射信号将传播更多的距离，例如100米[39]，从而产生更大的估计伪距。不幸的是，GPS接收机不能可靠地区分直接信号和反射信号。因此，多径和NLOS接收都成为城市地区GPS误差的主要原因。

为了了解GPS的实际性能，我们分析了两个真实世界的GPS数据集，这些数据集分别从配备GPS传感器的定期运营的公交车和几部现代智能手机中收集。有关我们的GPS数据集的更多详细信息，请参见第5.1节。这些GPS数据的定位误差统计数据如图2所示。由于公交车在市中心区域内沿预定路线行驶，我们发现GPS定位误差相对较大，第80个分位数误差为13.0米，平均误差为9.1米，如图2所示。尽管现代智能手机已经用先进的技术增强了它们的定位组件，例如基于无线信号的移动定位[24]，[30]，但我们仍然看到了相当大的误差，如图2所示，例如，平均和第80分位数误差分别为7.0米和11.9米。图3进一步展示了一个具体的例子，我们看到智能手机GPS接收器观测到的轨迹与实际轨迹有很大的偏差，平均定位误差高达12.3米。因此，迫切需要有效的技术来提高城市峡谷中的GPS精度。

2.3 Motivation

城市峡谷中GPS误差的根本原因是复杂动态的城市环境，特别是高层建筑引起的卫星信号反射。因此，我们认为GPS性能与GPS接收器周围的环境之间存在某种关系。这种假定是合理性的：一方面，对于由一对经纬度表示的给定位置，其周边环境因素对卫星信号的影响是长期一致的。另一方面，GPS卫星按一定周期有规律地运行，因此它们的位置是可以预测的[33]。因此，对于位置p，我们可以列举可用卫星的所有可能组合，包括卫星身份及其在天空中的位置，并且对于每个卫星组合，都将存在一个由GPS接收器估计的位置的观测值$\hat{p}$。可以通过映射函数$f$来建模实际位置$p$和GPS估计$\hat{p}$的关系，映射函数$f$被定义为：
$$f(p,c,s)\to \hat{p},$$
其中，$c$对$p$周围的城市环境进行编码，而$s$表示调用GPS定位时的卫星分布。在实践中，我们想从GPS估计$\hat{p}$中推断地面实况位置$p$，因此函数表示为$f(\hat{p},c,s)\to p$。

现有的工作[22]、[47]、[58]通常假设GPS误差，即$p$和$\hat{p}$之间的差，遵循高斯分布，而一些研究[64]报告称，GPS误差实际上遵循瑞利分布。事实上，高斯分布和瑞利分布都缺乏对大面积实际GPS估计建模的通用性。例如，Wu等人[58]必须为每个小路段的GPS估计拟合一个私有高斯分布。这些统计模型省略了重要的定位上下文，例如建筑物和卫星，因此不足以对映射函数$f$进行建模。

确实存在许多考虑建筑物和卫星信息以提高GPS性能的工作。他们使用专有的3D城市模型来近似函数$f$，方法是隐式地将位置$p$与可见卫星联系起来，或显式地跟踪$p$与观测卫星之间的信号路径。

• 对于前一类的研究工作，他们研究并扩展了阴影匹配的思想[23]、[49]、[60]、[63]、[68]，以提高定位精度。阴影匹配算法通过将卫星可见性与GPS接收器的测量值进行比较[23]，从候选位置中确定用户的位置。在给定初始GPS位置 $\hat{p}$ 的情况下，将 $\hat{p}$ 周围的一定区域均匀划分为网格，每个网格作为实际位置的候选位置。对于每个候选位置，该算法基于3D城市模型和卫星位置预测卫星能见度。如果给定卫星到候选位置的直接信号不能被障碍物（如建筑物）阻挡，则该卫星是可见的。同时，卫星能见度也可以通过GPS接收机的接收信号进行估计。由于反射的非视距信号可能导致不正确的能见度估计，阴影匹配算法通常假设接收信号强度大于预定义阈值的卫星是可见的。最后，将卫星能见度与基于信号的卫星能见度估计最匹配的候选位置视为阴影匹配的解决方案。

• 后一类的研究工作要么通过恢复“虚拟直接路径”来纠正伪距离[39]（例如，将实际路径恢复为图1中卫星B的红色虚线），要么计算候选位置的信号路径与观测到的信号路径之间的相似性[29]，[45]。

然而，基于阴影匹配的方法和基于卫星信号路径的方法都严重依赖于专有的3D城市模型，这些模型不容易获得。更糟糕的是，在阴影匹配中很难正确设置确定卫星能见度的阈值，而重新计算伪距可能会产生巨大的计算开销，这在很大程度上限制了它们在智能手机等普通设备上的实用性。

受深度强化学习理论的启发，该理论使用深度神经网络作为函数逼近器来学习Q函数[13]，我们建议使用强大的深度神经网络来逼近映射函数$f$，以更好地描述GPS估计和定位上下文之间的复杂关系，包括城市环境、卫星分布等。建立这样一个深度神经网络模型是可行的，也是有益的。

• 首先，由于深度学习[35]的强大表示能力，我们可以将粗略的上下文信息输入到深度神经网络模型中，这些信息对城市环境$c$和卫星分布$s$进行编码，而不是专有的3D城市模型。
• 其次，我们可以拥有丰富的GPS数据来很好地训练模型。由于GPS设备在车辆（如出租车和公交车）和智能设备（如智能手机）中的广泛应用，我们可以积累大量的GPS测量值作为训练样本[41]。
• 最后，尽管训练深度学习模型会很耗时，但推理速度极快[53]。与之前的工作[23]、[39]、[45]、[49]相比，基于深度学习的解决方案需要大量的3D城市模型存储和大量的实时计算，可以在云上训练和部署庞大的模型，并快速响应每个请求来修复GPS估计。

挑战。尽管具有很好的优势，但由于以下挑战，实现深度学习增强型GPS定位系统并非易事。

首先，建筑高度和卫星状态等多个关键因素可能会影响城市峡谷中的GPS性能，同时它们处于不同的模式和不同的维度。因此，如何在不丢失信息的情况下表示它们并将其正确地输入深度神经网络是一项挑战。

其次，位置通常表示为一对纬度和经度，由于搜索空间巨大，很难预测。因此，如何设计网络架构，包括输入和目标的形式，并利用更多机会来优化搜索空间，还有待探索。

第三，基于位置的应用程序通常需要跟踪感兴趣的对象。尽管我们可以调用该模型来固定每个单独的GPS估计，然而，这种方法效率低下，并且可能具有低精度。因此，如何使深度神经网络支持连续定位是一个挑战。

3 DESIGN OF DeepGPS

在本节中，我们将详细介绍DeepGPS的设计细节，并讨论如何扩展DeepGPS进行连续定位。

3.1 System Overview

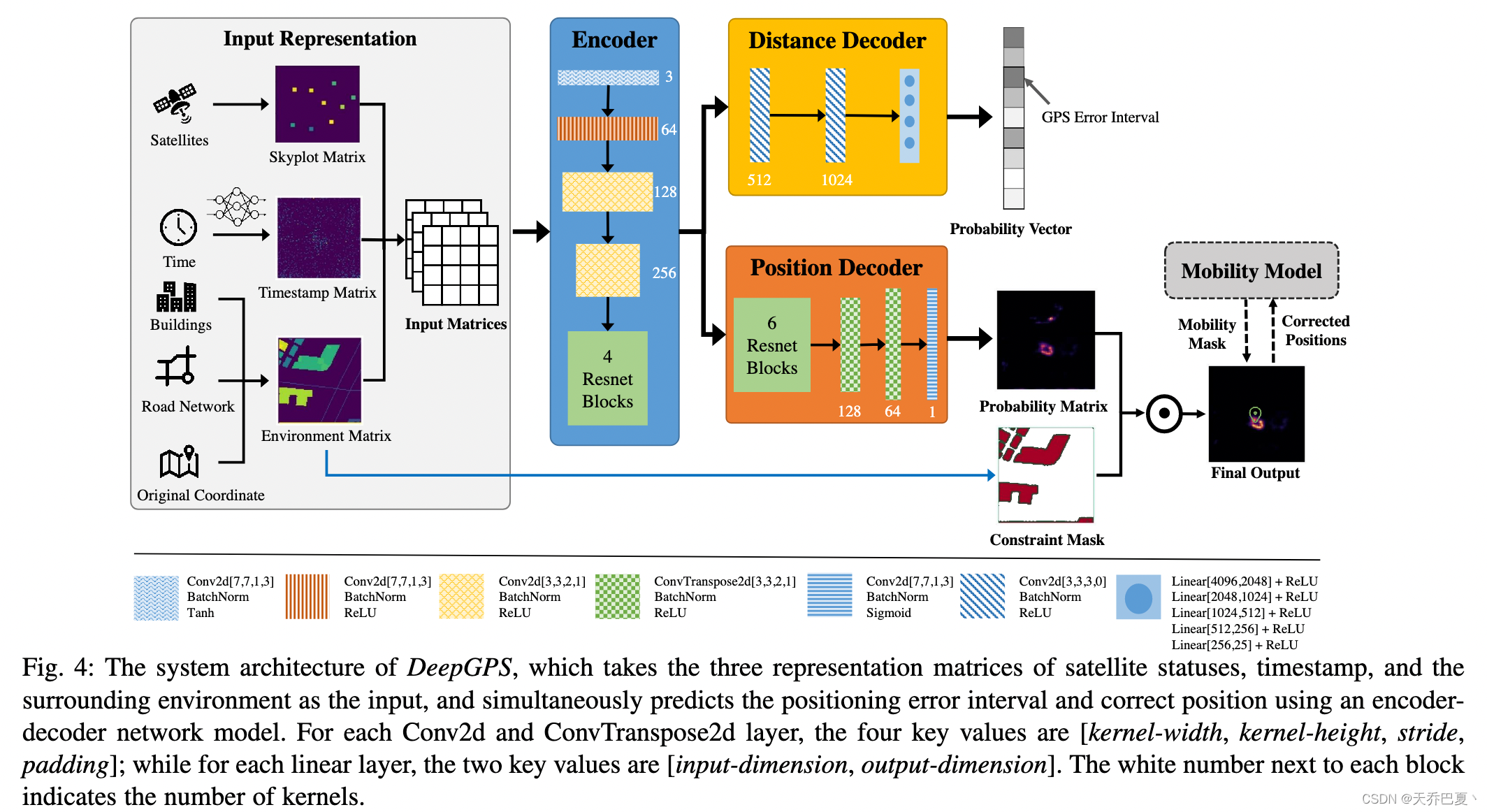
图4展示了DeepGPS的系统架构，它由四个主要模块组成：输入表示、编码器、距离解码器和位置解码器。在高层，DeepGPS融合了影响城市峡谷中GPS定位的多种因素，并以相同大小的矩阵表示。基于编码器-解码器网络设计，DeepGPS从输入矩阵中提取潜在特征，然后同时预测定位误差和给定GPS估计的正确位置。

• 输入表示模块（§3.2）考虑了卫星状态、定位时间和周围环境（即GPS接收器输出的原始坐标周围的道路和建筑物信息），并将其表示为矩阵。DeepGPS采用编码器-解码器网络模型来实现深度神经网络，用于逼近映射函数 $f$ （§3.3）。
• 编码器模块旨在从输入矩阵中提取高级特征。
• 距离解码器和位置解码器模块使用导出的特征图分别生成距离概率向量和位置概率矩阵。距离概率向量指示可能的定位误差，而位置概率矩阵指示当前GPS定位实例的正确位置。
• 此外，DeepGPS从环境矩阵中构建约束掩码，从位置概率矩阵中过滤出不可能的位置，并输出最终矩阵，其中值最大的位置是最终解。
• 此外，DeepGPS维护了一个从用户最新移动中学习的移动模型，并利用该模型来优化输出，以实现高效的连续定位（§3.4）。

3.2 Multi-Source Data Fused Input Representation

除了大气条件和多普勒效应的不一致性外，多种因素可能会影响城市峡谷中的GPS性能，这应被视为DeepGPS的输入。如第2.3节所述，城市峡谷中的GPS误差主要由卫星信号反射引起。原则上，单个物体是否被反射取决于卫星位置和GPS接收器周围建筑物的高度。在实践中，人们通常在城市地区的道路上行走或开车，因此道路信息对于限制用户的可能位置很重要。此外，还应考虑GPS定位实例的具体时间，原因如下。首先，人类的流动是有规律和一致的[66]，因此时间可以是城市动态的隐含指标，这可能会影响GPS定位。其次，导航卫星是定期运行的，时间也可以用来间接编码卫星分布的信息。总之，我们将卫星状态、时间和周围环境作为DeepGPS的输入。特别地，我们使用接收器提供的原始坐标附近的道路和建筑物的信息来描述环境。

我们更喜欢多源数据融合作为输入，而不是为每个输入数据源单独构建深度神经网络模型。这样的操作可以避免原始数据的信息丢失和多个模型的麻烦训练。为此，我们以相同大小的矩阵表示多源数据，这可以很好地捕捉感兴趣对象之间的空间关系。我们详细介绍了每个数据源的表示方式，如下所示。

(1) Representation of surrounding environment

周边环境转换为环境矩阵

当需要定位时，GPS接收器将以**[纬度、经度]的形式提供估计的位置$\hat{p}$，并提供估计位置不确定性的误差**。原则上，实际位置$p$在以估计位置$\hat{p}$为中心的圆内，其半径为GPS误差。因此，我们考虑了周围的环境，特别是建筑物的高度和布局以及道路的地理分布，以搜索实际位置p。

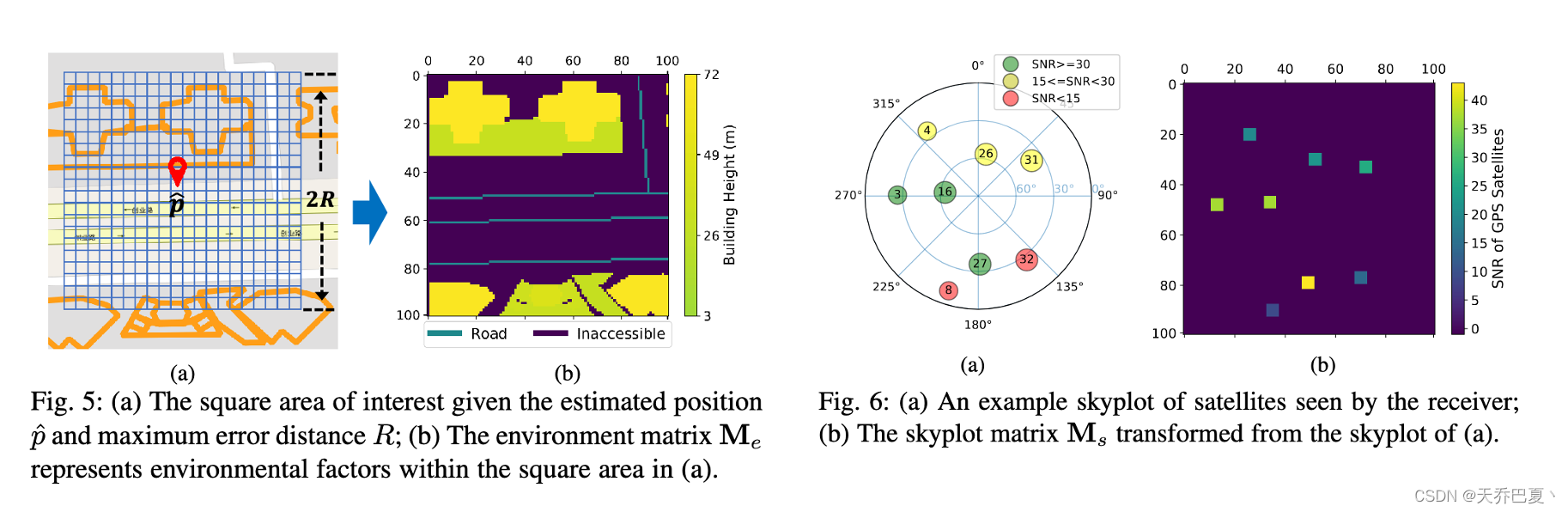
我们构建了一个环境矩阵$M_e$来表示这些可能影响该GPS定位实例的环境因素。我们首先选择一个以$\hat{p}$为中心，边长为$2R$的正方形区域，然后将该区域划分为大小为$c\times c$的单元格。这些单元格作为$p$可能所在的候选位置。正方形区域中的每个单元格对应于矩阵$M_e$的一个元素。对于矩阵中的每个元素，其值根据以下规则设置：

• i）如果该单元格是建筑的一部分，则其值设置为建筑高度；
• ii）如果小区是道路的一部分，则该值为零；
• iii）否则，它是$-1$，这意味着对应的小区是不可访问的。根据我们对大量GPS数据的分析，我们保守地设置R=50米，这大于99%的GPS误差，如图2所示。此外，我们将单元格大小设置为c=1米，以实现细粒度的位置固定。因此，矩阵$M_e$的大小为$100\times 100$。图5（a）展示了我们如何将目标区域划分为候选单元，并构建相应的环境矩阵$M_e$，如图5（b）所示。

(2) Representation of satellite statuses

卫星状态转换为天空图矩阵

除了估计的位置，我们还可以从接收器获得卫星元数据，其中包括每个卫星的方位角、仰角和信噪比（即SNR）。给定接收到的卫星元数据，可以绘制天空图来说明给定地面站点上的卫星几何形状[43]。图6（a）显示了一个示例天空图，该天空图是用我们在实地实验中收集的卫星元数据绘制的。每个圆圈代表GPS接收器检测到的卫星，数字作为卫星标识。每个圆圈的颜色表示卫星的信号强度：绿色表示非常好，黄色表示一般，而红色表示不好。

天空图是卫星状态的有效表示，以前的工作通常利用天空图来过滤非视距卫星[50]、[60]，或在3D城市模型的帮助下执行基于阴影匹配的位置固定[23]、[49]、[68]。因此，我们试图将天空图转换为矩阵，作为DeepGPS的部分输入。我们将此矩阵称为天空图矩阵$M_s$，因为它可以对所有检测到的卫星的相对位置和SNR值进行编码。我们将矩阵$M_s$设置为与$M_e$相同的大小，并将天空图上每个卫星的信息嵌入矩阵$M_s$中。首先，我们对齐天空图和$M_s$的中心。然后，对于每个检测到的卫星，利用卫星的高程和方位角将其位置从天空图映射到$M_s$。具体来说，卫星的仰角决定了其在矩阵$M_s$上的位置与$M_s$中心之间的距离，而卫星的方位角决定了与“向上”方向成正时钟方向的角度。如果矩阵Ms上的位置“有”卫星，则其值被设置为相应卫星的SNR值；否则，其值为零。图6（b）显示了图6（a）中示例天空图的天空图矩阵。

(3) Representation of timestamp

时间戳转换为时间戳矩阵

通常，GPS定位实例的时间戳表示为数字。根据GPS卫星的运行规则，每颗卫星每12小时绕地球一周，这意味着理论上它会周期性地返回同一个地方。然而，由于地球同时自转，在一个轨道周期后，从卫星到同一位置的接收器的相对位置可能不同。最近的研究[11]，[61]报告称，全球定位系统卫星的重访周期是可变的。具体而言，GPS卫星的重访周期略有不同，在240 s和250 s的范围内，每颗卫星的重访问周期都比一天稍早。此外，平均卫星重访周期比一天少246秒[11]。为了简单起见，我们将所有卫星的重访周期设置为86154 s（即24×3600−246）3，这意味着在这样的重访期之后，固定位置的接收器将再次“看到”相同的GPS卫星。基于GPS卫星的重访周期，我们从时间戳$t$生成时间戳矩阵$M_t$。

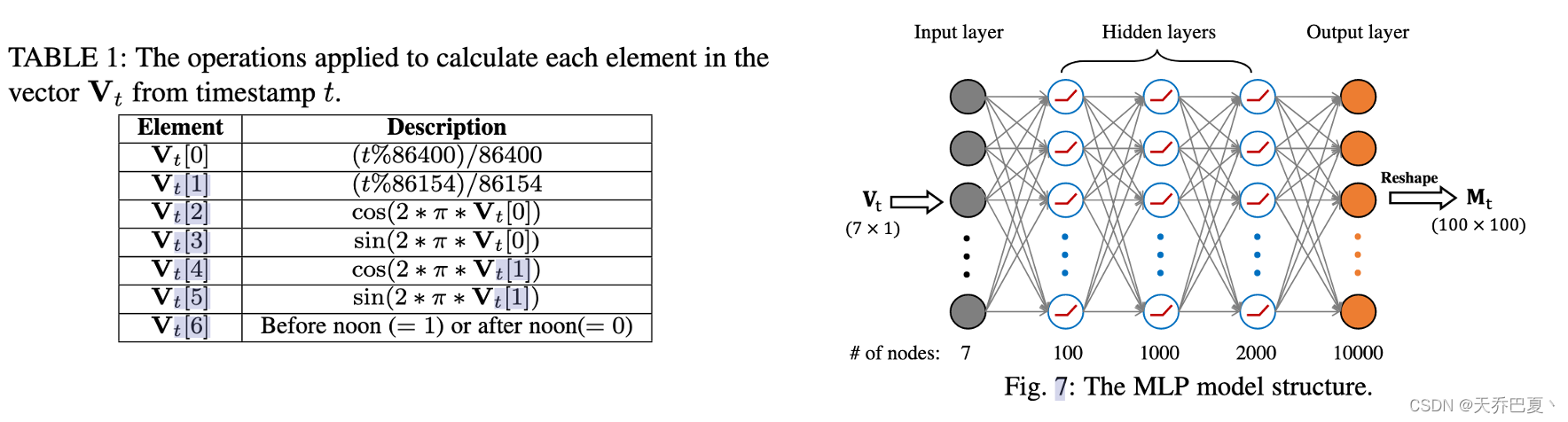
首先，我们将给定的时间戳$t$转换为7维向量$V_t$。向量$V_t$的每个元素都是从如表1所示的特定操作中导出的。具体而言，Vt[0]和Vt[1]分别代表地球自转周期和卫星重访周期的情况。请注意，重访期的总秒数设置为86154秒，自然日的总秒（即24小时）为86400秒。向量$V_t$的第3到第6个元素是将正弦和余弦应用于Vt[0]和Vt[1]的结果，这有助于快速找到周期[10]。此外，如果$t$是一天的中午之前，元素Vt[6]被设置为1，否则为0。

然后，我们应用一个简单的多层感知（MLP）模型将向量$V_t$转换为嵌入向量。MLP模型由五层组成，包括一个输入层、三个隐藏层和一个输出层。图7展示了MLP模型结构。具体地，输入层将7维向量$V_t$作为输入；三个隐藏层分别具有100、1000和2000个节点；而输出层将生成大小为10000的嵌入向量。此外，我们采用校正线性单元（ReLU）作为激活函数。导出的嵌入向量被重塑为与$M_e$和$M_s$具有相同大小100×100的矩阵。对于给定的时间戳$t$，我们将该矩阵称为时间戳矩阵$M_t$，这意味着GPS定位时间的周期性特征。

3.3 Deep Neural Network Design

给定这些输入矩阵，可以建立一个深度神经网络来直接预测正确的位置。然而，由于纬度和经度都是浮点数，搜索空间是无限的，这使得导出的模型很难训练和在实践中使用。相反，我们将目标输出设置为与输入矩阵大小相同的矩阵，并配置所需的模型来预测哪个单元格的正确位置。预测单元格的中心被视为固定位置。与此同时，我们实际上不需要校正所有的定位结果，因为许多GPS估计对于上层应用来说可能足够准确。因此，我们希望我们的模型也能预测定位误差，然后我们可以根据基于位置的应用程序的要求来确定是否固定当前的GPS估计。

为此，我们将所需的深度神经网络建模为编码器-解码器架构，其中两个解码器对编码器进行反馈，如图4所示。具体地，编码器$E$从输入矩阵（即$M_e、M_s和M_t$）中学习特征图$M$，并将$M$馈送到距离解码器$D_{dist}$和位置解码器$D_{posi}$，以分别预测定位误差和校正位置。双解码器设计的一个额外优点是，给定相同的特征图$M$，位置解码器和距离解码器可以相互绑定，并使它们的预测与接收器的观测和定位上下文最佳匹配。

Model structure

编码器：由于我们模型的输入是类似于图像的矩阵，因此我们构造了具有一系列2D卷积层的编码器E，以从由环境矩阵、天空图矩阵和时间戳矩阵表示的定位上下文中提取空间特征。此外，我们在编码器E和位置解码器$D_{posi}$中分别采用了4个和6个Resnet块，以形成一个深度神经网络，该网络可以同时探索足够的特征空间并避免梯度消失。

距离解码器：我们提出了距离解码器，$D_{dist}:M\to V_{dist}$，以在给定特征图M的情况下预测定位误差。解码器$D_{dist}$应用两个2D卷积层来处理M，然后将中间结果扁平化并馈送到四个线性层中，以导出最终输出$V_{dist}$。我们更倾向于预测一个误差区间，而不是预测一个可以建模为回归问题的精确误差。因此，我们将输出定义为$V_{dist}$概率向量，其中的每个元素对应于误差区间，其值指示概率。在我们的实现中，我们将间隔设置为2米，$V_{dist}$大小为25维，因为99%以上的GPS误差小于50米。因此，$V_{dist}$的第$i$个元素意味着误差在$(2\ast i，2\ast (i+1)]$米的范围内。

位置解码器：类似地，位置解码器，$D_{posi}:M\to R_{posi}$被设计用于从特征图M中预测正确的位置$p\prime$。如图4所示，$D_{posi}$与编码器E共享相似但相反的结构，编码器E首先将6个Resnet块应用于特征图M，然后使用两个2D转置卷积层来重新缩放中间结果，以一个2D卷积层结束。输出$R_{posi}$是与输入矩阵大小相同的矩阵，因此$R_{posi}$中的每个元素都对应于环境矩阵$M_e$中定义的候选单元。我们将目标位置设置为高斯峰值，而不是将包含地面实况位置的单元标记为1和其余0。因此，$R_{posi}$是一个概率矩阵，具有最大概率的元素暗示了地面实况位置的位置。与独热编码相比，高斯峰值表示有助于避免模型训练过程中的梯度消失[14]。

约束掩码：位置解码器$D_{posi}$可以预测任何细胞作为目标，然而，一些被建筑物或障碍物占据的细胞显然不能包含正确的位置。因此，我们提出了约束掩码$C_{env}$，它嵌入了周围环境的先验知识，以约束$D_{posi}$的输出。具体地，如果对应的单元不可访问，则$C_{env}$的元素被设置为0；否则设置为1，并且对应的单元格是有效的候选者。

Loss function

我们采用独热编码来为距离解码器$D_{dist}$准备目标向量$V_{true}$。对于每个GPS样本，我们使用GPS估计和实际位置计算其真实定位误差e，然后计算误差区间$j=\lfloor \frac{e}{2}\rfloor$，其中e落入该区间。然后，我们通过将$V_{true}$的第$j$个元素的值设置为1，将其余元素的值设为0，为该GPS样本准备目标向量$V_{true}$。由于我们将定位误差预测建模为一个分类问题，因此我们采用交叉熵损失来测量$D_{dist}$的输出$V_{dist}$和目标$V_{true}$之间的距离，该距离定义为：
$$L_{dist}=-\sum _{i=1}^n{b}_{i}log(p_i)$$
其中$b_i$是二进制指示符（如果第$i$个区间为真为1，否则为0），$p_i$是第$i$个区间的Softmax概率，n是$V_{dist}$的大小。默认情况下，我们将n设置为25。

对于位置解码器，我们利用均方误差损失（即L2范数损失）来测量增强输出$R_{env}$和目标$R_{true}$之间的距离，这是地面实况位置的高斯表示。因此，位置解码器$D_{posi}$的损失函数定义为：
$$L_{posi}=||R_{true}-R_{env}|{|}^2$$
其中$||\cdot |{|}^2$是L2范数损失。

最后，我们模型的总损失函数是$L_{dist}$和$L_{posi}$的加权和，即。，
$$L_{overall}=\lambda \times L_{dist}+L_{posi}$$
其中λ是正则化参数，用于平衡距离解码器和位置解码器对编码器的影响。为了确定λ的正确设置，我们分别训练$D_{dist}$和$D_{posi}$来观察它们的损耗，然后设置λ以使两个解码器的损耗很好地平衡。根据我们的实验，我们最终设置$\lambda =0.001$，这可以实现两个解码器的最佳预测性能。

Model training

我们利用大量标记的GPS样本，以及道路网络、建筑测量数据和卫星数据来训练DeepGPS。对于每个GPS定位实例及其地面实况位置，我们通过利用道路网络和建筑物高度的信息来构建环境矩阵$M_e$、来自定位时间的时间戳矩阵$M_t$和来自相应天空图的卫星矩阵$M_s$。此外，我们通过独热编码和矩阵$R_{true}$构建了25维的向量$V_{true}$，该矩阵将包含实际位置的单元标记为高斯峰值。向量$V_{true}$和矩阵$R_{true}$分别是距离解码器$D_{dist}$和位置解码器$D_{posi}$的目标输出。

在适当设置$\lambda$和损失函数$L_{overall}$的情况下，我们使用标记的GPS样本对网络进行整体训练。由于距离损失和位置损失加起来更新公共编码器，因此两个解码器可以相互访问彼此的信息，从而实现更准确的预测。值得注意的是，我们将MLP模型作为编码器E的一部分来处理，MLP模型将时间$t$转换为时间戳矩阵$M_t$，因此我们与编码器一起训练MLP模型。

3.4 Extend to Continuous Localization

有了足够的定位实例，就可以推断出用户的移动信息，这可以用来通过减少位置不确定性来进一步改进位置固定。具体而言，DeepGPS引入了一个移动模型，如图4所示，该模型旨在粗略估计用户的移动速度，并利用该速度计算可达区域以约束未来的定位。

Mobility model

移动性模型。DeepGPS利用最新的k个校正定位实例，特别是位置$(p_{i-1}^{\prime },...,p_{i-k}^{\prime })$和相应的定位时间$(t_{i-1},...,t_{i-k})$，来推断用户的移动。为了简单和通用，DeepGPS只估计用户的平均移动速度$v$，因为其他移动信息，例如移动方向，需要额外的传感器数据。对于给定的用户，DeepGPS通过以下等式使用最新的k个定位实例不断更新平均速度$v$：
$$v=\frac{{\sum }_{j=1}^{k-1}\frac{L\left(p_{i-j}^{\prime },p_{i-j-1}^{\prime }\right)}{t_{i-j}-t_{i-j-1}}}{k-1}$$
其中$L\left(p_{i-j}^{\prime },p_{i-j-1}^{\prime }\right)$计算位置$p_{i-j}^{\prime }$和$p_{i-j-1}^{\prime }$之间的距离。当速度计算的位置不足时，我们将k设置为初始使用的可用数字。

Mobility improved position fixing

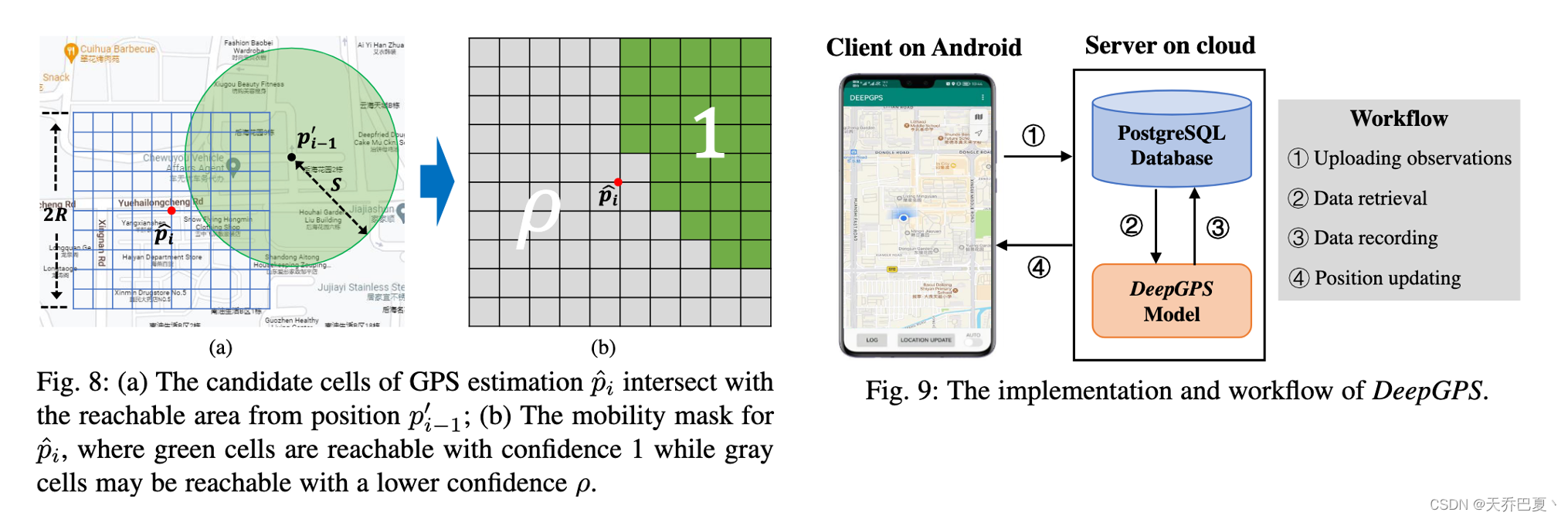
移动性提高了定位能力。一旦平均移动速度$v$准备好，我们就可以导出用于位置校正的额外移动性约束。对于GPS估计的位置${\hat{p}}_i$，一方面，我们构建了一个边长为$2R$的以${\hat{p}}_i$为中心的正方形区域，并将该正方形区域划分为大小为$c\times c$的单元。另一方面，构建了以位置$p_{i-1}^{\prime }$为中心的圆，即最后一个定位实例的校正位置，其半径为$S=v\times ∆t$，其中，$∆t$是定位${\hat{p}}_i$的时间$t_i$和定位${\hat{p}}_{i-1}$时间$t_{i-1}$之间的时间差。圆圈区域根据用户最近的移动速度指示用户的可到达区域。结合GPS位置和可达区域，正方形区域和圆形区域的交叉点中的单元格最有可能包含正确的位置，而正方形区域的其他单元格则不太可能。基于这种直觉，我们构造了一个矩阵，称为移动掩码$C_{mob}$，其每个元素对应于正方形区域中的一个单元。具体地说，如果单元格（或部分）被圆圈覆盖，则其值设置为1；否则，我们将其值设置为$\rho (0\le \rho <1)$，这意味着该单元格可能包含置信度为$\rho$的正确位置。值得注意的是，如果我们设置$\rho =1$，我们实际上禁用了移动性改进的定位功能。图8举例说明了一个使用移动信息和GPS估计来确定移动掩码的例子。

移动掩码将在约束掩码之后生效，而不是将约束掩码和移动掩码一起应用于位置解码器的原始输出。背后的原因是，我们可以使移动性模型独立于深度神经网络，从而减轻模型训练的开销。因此，我们将移动掩码$C_{mob}与R_{env}$点乘，$R_{env}$是将约束掩码应用于位置解码器的原始输出的处理结果，然后导出最终的概率矩阵$R_{mob}=R_{env}\odot C_{mob}$，根据迁移率信息对其进行校正。最后，输出$R_{mob}$中具有最大值的单元的中心作为DeepGPS的校正位置。

事实上，我们的移动模型可以通过更丰富的移动数据和先进的跟踪技术得到进一步增强。例如，如果用户智能手机的惯性测量单元（IMU）传感器数据可用，我们可以获得更多关于用户的移动信息[62]，例如移动速度和方向，并利用更先进的技术，例如粒子滤波器[59]来跟踪用户的移动，从而细化可到达区域，以大大降低位置的不确定性。我们把这项研究作为我们未来的工作。

4 IMPLEMENTATION

我们在云（作为服务器）和几个Android智能手机（作为客户端）上设计并实现了一个原型，如图9所示。Android客户端收集原始GPS测量值并将其上传到云服务器，云服务器负责预测误差距离和正确位置。我们详细介绍了每个组件的实现和整个工作流程，如下所示。

Android上的客户端。我们在使用Android操作系统的智能手机上实现了客户端组件，这使我们能够通过Android API轻松访问原始GPS测量结果（包括GPS估计位置和误差、卫星元数据等）[2]。客户端可以记录原始GPS测量值以进行数据分析。如果用户需要在城市峡谷中进行更准确的定位，她可以触发“LOCATION UPDATE”按钮来修复GPS估计，这是由云上的DeepGPS模型支持的。如有必要，用户还可以通过打开“AUTO”选项来启用自动位置更新功能，这将允许DeepGPS分析用户的粗略移动信息，以进行连续定位。

云上的服务器。我们在PyTorch 1.8.1（CUDA 11.1）[7]中实现了DeepGPS模型，服务器的CPU为Intel（R）Core（TM）i7-10700K 3.80GHz，GPU为RTX3090，内存为48GB。为了训练我们的模型，我们使用Adam作为优化器，并将学习率α=1e−5和批量大小设置为128。此外，我们在云上部署了DeepGPS模型，用户可以随时随地访问定位服务。云部署还将减轻智能手机客户端的计算和存储开销[37]。

在服务器端，我们还维护了一个空间数据库，该数据库在PostgreSQL[6]中使用空间数据库扩展程序PostGIS[5]实现，用于高效的数据查询。空间数据库用于存储测试城市的道路网络和建筑测量数据（例如，建筑物的高度和边界）。

空间数据库与DeepGPS模型交互，用于数据检索和记录。一方面，在给定来自客户端的估计位置的情况下，DeepGPS可以检索到围绕位置的道路网络和建筑信息，以构建环境矩阵。另一方面，当用户启用连续定位时，DeepGPS会将用户的历史定位数据记录到数据库中，以动态更新该用户的移动模型。

工作流程。如图9所示，DeepGPS根据每个请求执行位置固定，如下所示。

① 当需要精确定位时，客户端首先通过安卓API获取GPS估计位置 $\hat{p}$ 和其他卫星元数据，然后将这些数据（包括 $\hat{p}$ 、时间戳t和卫星元数据）和误差阈值δ传达给服务器。注意，阈值δ是可选的，用户可以让DeepGPS始终校正GPS估计。如有必要，可以通过一些基于位置的应用程序根据其对定位精度的要求来指定阈值δ。

② 在接收到请求后，DeepGPS模型从空间数据库中检索位置 $\hat{p}$ 周围的道路网络和建筑物的数据，然后通过利用多源数据分别构建环境矩阵$M_e$、时间戳矩阵$M_t$和卫星矩阵$M_s$。一旦这些输入矩阵准备就绪，并且提供了δ，则模型将首先利用距离解码器$D_{dist}$来预测可能的误差e。如果e小于阈值δ，DeepGPS会将 $\hat{p}$ 视为正确的位置$p^{\prime }$，因为 $\hat{p}$ 对于用户的应用来说足够准确。否则，DeepGPS调用位置解码器$D_{posi}$来预测正确的位置$p^{\prime }$。由于我们无法知道地面实况位置，DeepGPS在预测正确位置后没有进一步的操作。如果没有提供δ，则直接执行$D_{posi}$来推断$p^{\prime }$。

③ 一旦处理了定位请求，DeepGPS就会将一条记录$<t，\hat{p}，p^{\prime }>$记录到数据库中。该记录表明请求者在时间$t$访问了位置$p^{\prime }$，并将被附加到请求者的特定文件中。这些记录有助于DeepGPS动态更新给定用户的移动模型。

④最后，服务器将位置$p^{\prime }$发送回客户端。

5 PERFORMANCE EVALUATION

在本节中，我们使用大型公交车GPS轨迹数据集和使用Android客户端收集的实时GPS测量值来评估DeepGPS的性能。

5.1 Experiment Setup

我们在中国深圳市进行了所有实验，深圳拥有世界第二多的摩天大楼[9]。

Dataset

我们收集了五种不同类型的数据用于绩效评估。具体而言，道路网络和建筑测量数据用于表示定位环境，卫星数据描述卫星的分布和状态。此外，我们将公交车轨迹数据和现场GPS测量作为模型训练和测试的定位实例。

1. 道路网络。我们从OpenStreetMap（OSM）[4]下载深圳市的道路网络。OSM文件以节点（即点）、方式（即道路）和关系（即POI的属性）的形式包含我们测试城市的所有道路和兴趣点（points-of-interest POIs），例如湖泊和草地。特别是，我们可以利用关系来区分给定单元格是否可访问。

2. 建筑调查数据。我们从合作者那里获得建筑调查数据。此测量文件与OSM文件的格式相似，包含有关深圳市所有建筑的布局、高度和特性的信息。具体来说，节点列表是端到端连接的，以形成每个建筑的轮廓，而高度和建筑属性（例如名称）则以关系标记。这些数据有助于我们识别城市中的建筑高度和人迹罕至的区域。

3. 公交车轨迹数据。配备GPS设备的公共巴士可以定期向运营中心报告其状态。一般来说，深圳市的公交车按照固定的路线和时间表定期运行，每5秒发送一次报告[56]。每个报告都包括时间戳、GPS位置、行驶速度、方向、状态等。我们准备了一个公交车GPS轨迹数据集，该数据集由16690辆公交车于2020年6月12日收集，覆盖1845条路线。这些公交线路覆盖了深圳市的大部分城区。我们总共有41540968份公交车报告。

4. 实时GPS测量。通过在智能手机上安装我们的Android客户端（见第4节），五名志愿者驾驶私家车每5秒收集一次GPS测量值，沿着深圳市南山区市中心的一些计划路线行驶。他们的智能手机包括华为Mate 10 pro、Mate 30 pro、Mate 40 pro和三星Galaxy Note 5。最后，我们收集了16814个有效的定位样本。

5. 卫星数据。我们的Android客户端可以收集卫星元数据，因此在采集定位样本时，真实的现场GPS数据集包含卫星信息。然而，这些巴士报告不包括卫星元数据。为了弥补这一点，我们访问了CelesTrak[1]，以检索给定每个总线报告的时间戳和实际位置的历史卫星元数据。因此，我们可以用相应的卫星数据补充所有总线报告。

Ground truth collection

地面实况收集。与之前的工作[22]、[53]、[58]类似，我们使用先进的基于隐马尔可夫的地图匹配算法[47]将公交车轨迹的GPS序列和实时GPS测量映射到路段。由于公共巴士和测试车辆都沿着规划的路线行驶，我们可以利用这些先验知识来验证地图匹配结果，并手动纠正这些错误的匹配结果。最后，对于每个GPS估计位置$\hat{p}$，我们将其在匹配路段上的投影视为地面实况$p$。

Testing regions and model training

测试区域和模型训练。由于我们的目标是提高城市峡谷中的GPS性能，因此我们选择了深圳市南山区、福田区和宝安区这三个市中心区作为我们的测试区域。这三个地区拥有深圳市最密集的高层建筑，我们将它们分别表示为区域N、区域F和区域B。我们还收集了N区域的实际GPS测量值。

我们保留了属于这三个区域的公交车报告，以便进行实验。考虑到不同的地区有不同的环境，因此我们使用每个地区自己的公交车报告为每个地区训练一个专门的DeepGPS模型。对于每个区域，我们使用70%的公交车报告来训练其模型，同时保留剩余的30%用于测试。所有现场GPS数据仅用于测试。此外，我们稍后将使用三个区域的数据训练的统一模型与这些定制模型的性能进行比较。

Performance metrics.

我们定义了以下三个指标来评估DeepGPS的性能。

• 精度。预测精度被定义为模型输出的位置与地面实况之间的平均距离。
  $$accuracy=\frac{1}{N}\sum _{i=1}^{N}L(p_i,p_i^{\prime }),$$
  其中N是GPS样本的数量，$p_i$和$p_i^{\prime }$分别是第$i$个地面实况和正确位置，而函数$L(p_i,p_i^{\prime })$返回它们之间的距离。

• 有效比率。除了精度之外，我们还定义了有效比率来评估DeepGPS相对于原始GPS估计的定位改进。具体而言，我们将有效比率定义为DeepGPS预测的正确位置比GPS估计的位置更接近地面实况的样本的比例，即
  $$ratio=\frac{{\sum }_{i=1}^N\mathbb{I}(L(p_i,p_i^{\prime })<L(p_i,{\hat{p}}_i))}{N}\times 100\%$$
  其中，如果条件$a$为真，则指示函数$\mathbb{I}(a)$将返回1；否则为0。

• 预测错误。由于我们的模型可以预测定位误差距离，因此我们定义了平均预测误差来评估DeepGPS，如下所示：
  $$\text{ error }=\frac{{\sum }_{i=1}^N\left|\arg \max \left({\mathbf{V}}_{dist}^i\right)-\arg \max \left({\mathbf{V}}_{\text{true }}^i\right)\right|}{N}\times 2$$
  其中argmax（V）返回向量V中最大元素的索引。回想一下，向量V中的每个间隔对应于2米，因此将平均索引偏移乘以2来得出预测误差。

我们使用精度和有效比来评估位置解码器$D_{posi}$的有效性，同时利用预测误差来评估距离解码器$D_{dist}$。在下面的实验中，我们设置λ=0.001和δ=0，以强制位置解码器校正每个GPS估计。默认情况下，我们为移动率模型设置k=5和ρ=0.4，并为单元大小设置c=1米。

5.2 Evaluation on Bus Data

Overall performance

对于每个测试区域，我们使用在该区域收集的GPS样本来训练定制模型。此外，我们基于三个区域的训练数据训练了一个统一的模型。为了研究DeepGPS的泛化能力，我们还将一个区域的模型应用于其他两个区域进行交叉验证。在本小节中，我们已经禁用了用于实验的移动性模型。

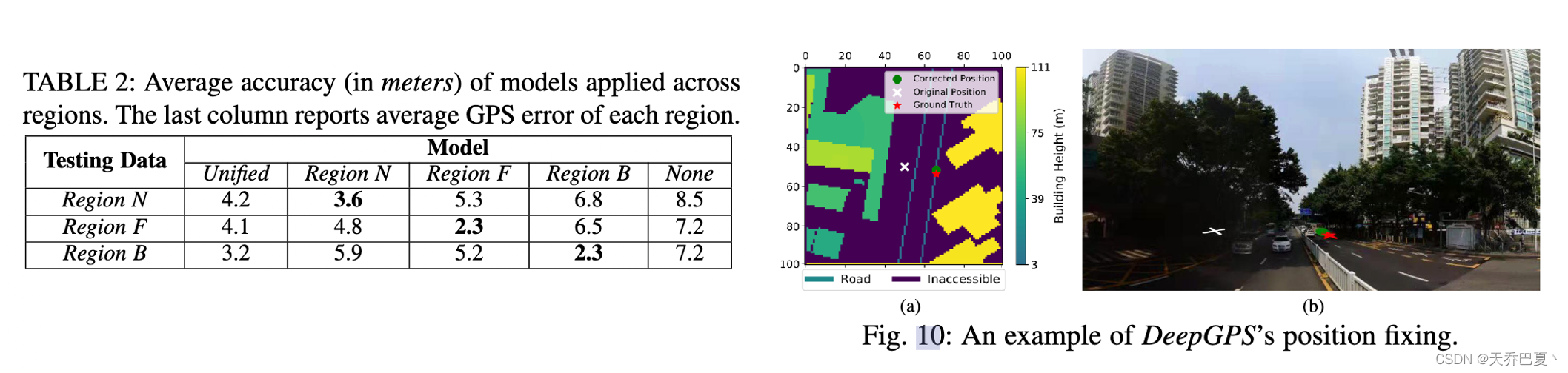
如表2所示，我们发现统一模型对三个区域实现了较高的定位精度，精度分别为4.2米、4.1米和3.2米。与统一模型相比，定制模型的精度要高得多。具体而言，每个定制模型在其自己的区域上实现了最佳精度，例如，在区域N、区域F和区域B的数据集上训练的模型的最佳精度结果分别为3.6米、2.3米和2.3米。尽管我们仍然观察到跨区域应用的相对较高的精度。例如，针对区域N训练的模型在区域F的测试数据上实现了4.8米的平均精度，这比区域F的平均GPS误差（即7.2米）好得多。这些结果表明，DeepGPS模型具有良好的通用性，如果使用目标区域的样本进行专门训练，则可以获得最佳性能。与原始GPS误差相比，DeepGPSim对GPS定位的验证率为57.6%，

图 10 演示了一个具体示例，其中 DeepGPS 正确修复了 GPS 估计。由于周围建筑物的影响，GPS错误地将用户定位在相邻路段上，如图10（a）所示。我们进一步手动调查定位环境，如图10（b）所示，这是我们测试城市中的一个典型街道峡谷。

我们观察到有效比率和预测误差有类似结果，分别如表3和表4所示。从表3中的实验结果可以看出，尽管统一模型可以在三个区域实现较高的有效配给，即平均有效率为85.3%，但每个定制模型在目标区域的有效率最高，平均有效率为90.1%。即使自定义模型是在一个区域的样本上训练的，并用于校正其他区域的GPS估计，DeepGPS仍然表现良好，有效率大于72.0%。表3中的结果表明，在大多数情况下，DeepGPS可以获得比GPS原始输出更好的校正位置。

表4给出了DeepGPS的距离解码器$D_{dist}$的评估结果。我们发现预测误差很小，即1.4～4.1米。特别地，如果我们在同一区域上训练和测试DeepGPS模型，则平均预测误差仅为1.7米，这对应于仅在25维向量$V_{dist}$中的一个区间偏移。因此，$D_{dist}的表现相当不错。根据以上实验结果，我们发现DeepGPS具有良好的通用性和定位性能。平均而言，DeepGPS将GPS定位精度提高了64.6%，在90.1%的情况下可以有效校正GPS估计。

Effect of building heights

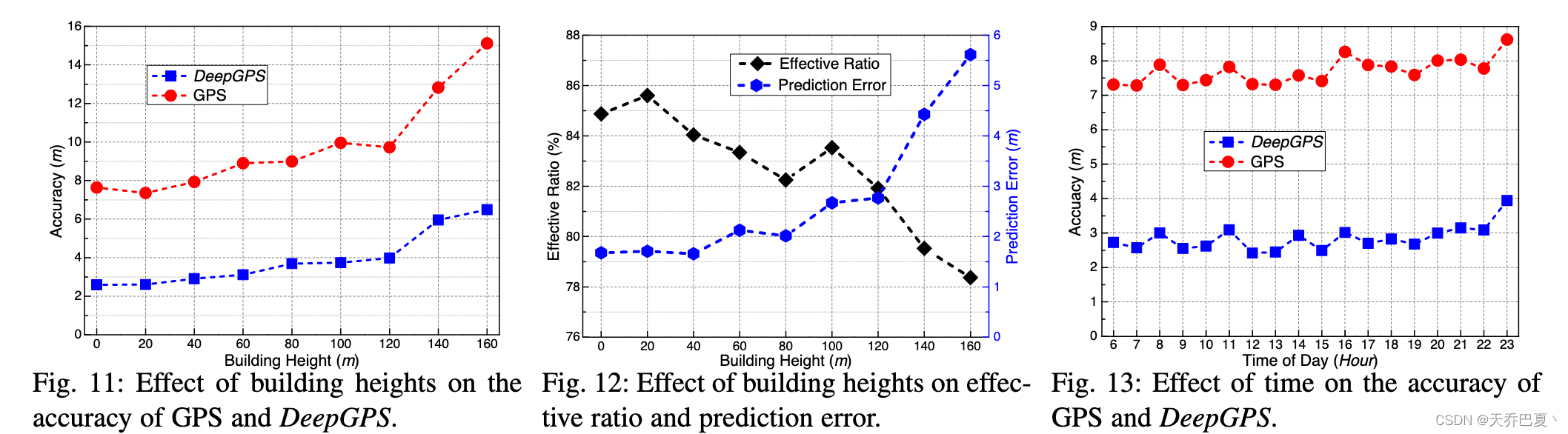
我们通过利用包含建筑高度信息的环境矩阵$M_e$，探讨了建筑高度对城市峡谷定位性能的影响。对于每个GPS样本，我们将GPS接收器周围的建筑高度计算为$M_e$中元素的平均值，这些元素的值大于零。图11比较了GPS和DeepGPS在不同建筑高度下的定位精度。注意到x轴的每个值x指示建筑物高度的范围，[x，x+20）米。通常，较高的建筑物更有可能反射甚至阻挡卫星信号，从而显著影响定位。当接收器周围有较高的建筑物时，GPS和DeepGPS的精度结果都会变差。然而，DeepGPS仍然比GPS表现更好，定位误差要小得多。

如图12所示，我们观察到建筑高度也会影响DeepGPS在有效比率和预测误差指标上的性能。一般来说，较高的建筑物会导致DeepGPS的有效比率降低，同时增加预测误差。

Effect of positioning time

我们还研究了时间对GPS和DeepGPS精度的影响，并将结果绘制在图13中。我们看到，这两个系统的准确性在一天中的不同时间略有不同。DeepGPS始终比GPS工作得好得多。此外，我们在图15中观察到有效比率和预测误差这两个指标的变化趋势相似。从这两张图中，我们观察到DeepGPS在几个小时内（例如上午11点和晚上11点）的性能略有下降。然而，原因还有待进一步探讨。

5.3 Evaluation on Real-field Data

在本小节中，我们将利用现场GPS测量来进一步评估DeepGPS。具体来说，我们将研究每个模型组件的性能以及一些重要参数的影响。

Visualization

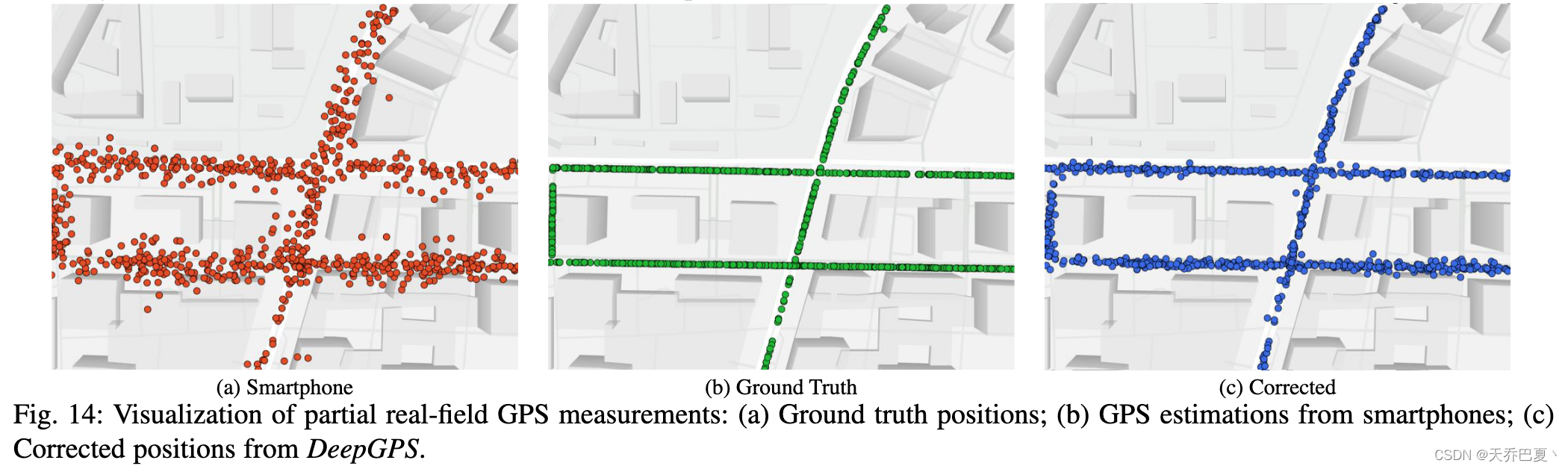
我们在N区的街道峡谷中使用现代智能手机收集原始GPS测量值，并在图14中可视化部分GPS数据。与图14（a）所示的地面实况位置相比，智能手机的GPS估计非常嘈杂，与地面实况的偏差很大。相反，DeepGPS可以有效地纠正这些错误的GPS估计，如图14（c）所示。除了离散位置的比较外，图3还比较了三个完整的轨迹，即地面实况轨迹、智能手机轨迹和DeepGPS的校正轨迹。图3显示，DeepGPS通过将误差从12.3米大幅降低到5.2米，从而提高了GPS性能。

Impact of different model components

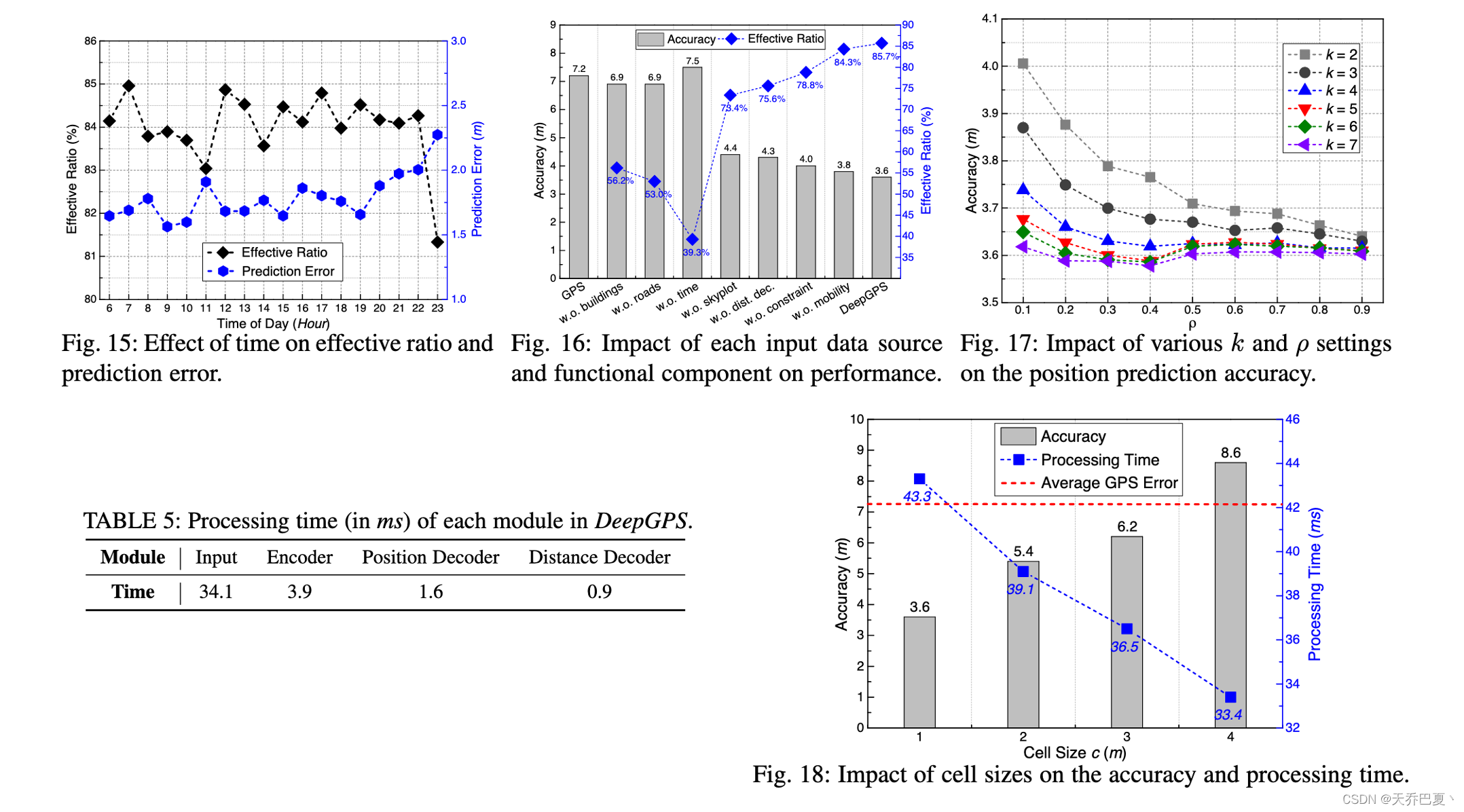
不同模型组件的影响。为了了解输入数据源和功能组件如何影响DeepGPS的性能，我们进行了各种消融实验。我们将GPS性能作为基线，并采用不同的系统设计进行比较。在接下来的实验中，我们移除每个组件并训练剩余的模型。所有变体模型分别使用相同的训练和测试数据集进行训练和测试。结果如图16所示，其中“w.o.”是without的缩写，“dist.dec.”代表距离解码器。

通常，我们发现这些输入数据，即建筑高度、道路信息和时间戳，对DeepGPS的性能的影响比其他模块（如约束掩码和移动性模型）大得多。如果我们省略建筑物或道路信息的输入，DeepGPS的性能将严重下降到6.9米，精度与GPS误差相似，有效率小于60%。因此，证明了环境是影响城市峡谷GPS定位性能的重要因素。

从图16中，我们惊讶地发现，时间对定位性能的影响最大。在不输入时间戳矩阵的情况下，DeepGPS的精度将下降到7.5米，甚至比GPS误差更大（即7.2米），而有效率低至39.3%。这种现象可以解释如下。在城市峡谷中，多径和非视距卫星是GPS性能下降的主要原因。对于特定地点的GPS接收器来说，接收到的GPS信号是否被反射主要取决于周围的建筑物和卫星的分布，即接收器可以观察到的卫星几何形状。考虑到GPS卫星是周期性运行的，因此，当接收器周围的环境保持不变时，由于卫星几何形状的近似重复，该位置的多径和非视距卫星具有固有的可重复性特征[19]。图16显示了天空图也会影响DeepGPS的性能。然而，与其他输入数据源相比，其影响有限，准确度和有效率分别降至4.4米和73.4%。与天空图相比，时间戳是一个更关键的因素，可以捕捉卫星几何形状和定位性能之间的重要关系。

在我们的深度神经网络模型中，我们使用距离解码器和位置解码器一起训练编码器，图16中的结果也证明了距离解码器的有效性，它将精度从4.3米提高到3.6米。它证实了距离解码器可以通过在位置预测上添加隐式约束来影响位置解码器。

我们提出了两种功能掩码，即约束掩码和移动掩码，以进一步改进DeepGPS。约束掩模利用环境信息来完成地图匹配等工作，并通过过滤掉不可能的单元格来减少定位误差，精度提高了10%。此外，移动掩码进一步将DeepGPS的精度提高了约5%。

Impact of k and ρ

移动性模型利用最新的k个校正定位来计算用户的移动速度，并为无法到达的小区分配置信度ρ。因此，我们进行了实验来研究k和ρ对定位精度的影响。如图17所示，当我们使用更正确的位置，即增加k来进行速度计算时，对于给定的ρ，精度通常会增加。然而，当k≥5时，更多的定位样本带来的精度提高可以忽略不计。

随着置信度ρ的增加，对于k≤5的设置，精度增加；对于其他k值，当ρ≤0.4时，定位精度增加，但随着ρ的增大，定位精度会变差。当速度计算不够准确时（例如，在k≤5个样本的情况下），DeepGPS倾向于平等对待所有候选小区，倾向于选择更大的ρ来获得更好的定位精度。当我们能够准确估计移动速度时（即，在k≥5个样本的情况下），用户的实际位置应该很可能在可到达区域覆盖的这些单元格中（即，图8中置信度为1的绿色单元格），因此我们需要一个小的ρ来过滤掉不可到达的单元格。然而，ρ值太小（例如，0.1）意味着DeepGPS将盲目相信移动性模型，并可能错误地过滤掉某些定位实例的正确小区，这些定位实例偶尔会落在无法到达的小区中。因此，ρ太小有点激进，会损害定位精度。另一方面，较大的ρ值会削弱移动掩码的过滤能力，并错误地选择一些无法到达的小区作为输出，从而降低定位精度。从图17中，我们得出结论，k=5和ρ=0.4是很好的设置，可以在避免额外计算的同时实现最佳精度。

Processing time

我们评估了DeepGPS的效率，并在表5中给出了四个关键模块的平均处理时间。为了处理每个请求，输入模块花费最多的时间，例如34.1ms来构建三个矩阵，而编码器或任何解码器的处理时间都很短，例如＜4ms。此外，通过搜索最终输出矩阵中具有最大概率的元素，将花费数毫秒来导出正确的位置。DeepGPS校正GPS估计的总处理时间约为43毫秒。作为一个明确的比较，最先进的方法Gnome[39]需要几秒钟来校正GPS估计（不包括离线预计算的时间），该方法基于3D建筑模型和卫星位置重新计算伪距以进行位置校正。因此，训练用于推断正确位置的深度学习模型是有效的。

Impact of cell size

图18显示了在单元大小c的各种设置下的定位精度和端到端处理时间。通常，较大的单元可以减少输入矩阵的大小，从而减少整个处理时间。然而，它们同时会带来更大的定位误差。例如，4 m×4 m单元导致定位误差为8.6米，这比GPS误差大。相反，1米×1米的单元将精度提高到3.6米，而代价是仅增加10毫秒的延迟。由于增加的处理时间很小，因此DeepGPS采用了1 m×1 m的单元，以获得更好的定位性能。

6 RELATED WORK

为了提高城市地区的全球定位系统精度，我们付出了巨大的努力。车辆可以结合各种技术，例如地图匹配[47]、[53]和航位推算[31]，以及GPS估计，将其位置映射到路段。行人用户可以在智能手机上利用蜂窝/WiFi信号[24]、[30]、惯性传感器[15]、[62]、磁罗盘[55]和气压计[26]来增强定位。目前已经提出了其他技术，如协作GPS[17]和差分GPS[25]，通过在多个接收器之间共享定位信息来提高GPS精度。例如，Chen等人[17]提出了BikeGPS，通过在一组自行车之间共享GPS接收，实现共享自行车在城市峡谷中的精确定位。然而，这些工作需要额外的传感器或多个GPS接收器之间的协作。此外，它们不会应对城市峡谷中GPS误差的根本原因，即非视距卫星信号。

先前的工作探索了非视距信号接收的缓解方案，可分为三类，基于名称追踪的方法[21]、[67]、基于阴影匹配的方法[20]、[23]、[49]、[50]、[60]、[63]、[68]和基于卫星信号路径的方法[29]、[39]、[45]、[48]。第一类[21]、[67]的研究将射线跟踪算法应用于卫星信号以校正伪距误差。例如，Zhang等人[67]提出了一种3D地图数据库辅助的基于GNSS的协同定位方法，该方法利用光线跟踪算法来校正每个GPS接收器的NLOS伪距，并采用因子图优化技术来协同优化多个接收器之间的定位。然而，这种方法依赖于3D建筑模型和多个GPS接收器之间的协作。对于高质量的光线跟踪，一些方法需要使用专用硬件重建街道建筑的反射表面，例如全景相机[54]或激光雷达[57]。

在第2.3节中，我们讨论了基于阴影匹配的方法和基于卫星信号路径的方法，它们利用专有的3D城市模型和实时卫星信息来明确校正GPS估计。作为前一类的代表作，Ng等人[49]使用机器学习分类器为智能手机实现阴影匹配，以区分视距和非视距卫星。然而，基于阴影匹配的方法主要依赖于精确的3D城市模型，移除非视距卫星可能会减少可用卫星读数的数量，并且无法计算接收器的位置。此外，后一类的最新工作Gnome[39]使用谷歌街景的全景图像来调整3D城市模型的建筑高度，然后通过利用这些建筑数据从候选网格中估计真实位置。Gnome严重依赖第三方资源，而这些资源并不是广泛可用的，并且会产生巨大的计算开销。因此，3D建筑模型的有限可用性将在很大程度上限制这些方法的实际应用。

随着GPS轨迹数据[70]的广泛可用，许多工作试图从统计学的角度测量和校准GPS误差[28]，[42]，[46]，[51]，[58]。例如，Ma等人[42]使用历史公交车GPS轨迹数据评估城市路段的GPS环境友好性。Wu等人[58]假设GPS误差遵循高斯分布，并基于专门从路段的GPS数据中学习的统计模型，将单个GPS位置定位到该路段。与这些工作不同的是，我们利用大量的GPS样本来训练深度神经网络，该网络将GPS估计转换到正确的位置，并可以为大城市地区服务。

7 DISCUSSION

在本节中，我们将讨论DeepGPS的性能比较、实现、更新和数据发布等问题。

与其他工作的准确性比较。以前的工作严重依赖于精确的专有3D建筑模型，这些模型不容易访问，因此，我们无法实现直接性能比较的现有方法。相反，我们根据他们的实验结果总结了他们的平均定位精度，并将DeepGPS与上一节中提到的关于定位精度性能指标的三部代表作[39]、[49]、[67]进行了比较。如表6所示，我们发现DeepGPS显著优于现有方法，实现了更好的定位精度，例如，精度分别提高了53.8%、40.0%和41.9%。

在智能手机上部署。在智能手机上部署DeepGPS时，我们必须解决两个关键挑战。首先，DeepGPS的执行取决于一个训练有素的模型，该模型的大小有点大，即大约170MB，以及其他资源，例如道路网络和建筑测量数据，这些数据通常都是大尺寸的。例如，深圳市的道路网络文件约为344MB，建筑测量数据约为420MB。因此，DeepGPS的部署至少消耗934MB的内存，这对于普通智能手机来说是一个相对巨大的存储开销。其次，DeepGPS将产生相当大的计算成本。给定定位请求，系统需要查询道路网络和建筑测量数据，以检索初始GPS位置周围的环境信息，然后计算环境矩阵、天空图矩阵和时间戳矩阵。然后，将这三个矩阵输入到模型中，以推断定位误差并校正位置。目前，我们将这些计算留给功能强大的服务器，而不是智能手机。

未来，我们将研究如何通过研究一些先进的模型压缩技术来压缩深度神经网络模型，同时保持其性能[38]。此外，我们发现GPS实际上在大多数地区都表现良好，除了那些高层建筑密集的地区。因此，我们可以对整个城市的GPS误差分布进行调查，并确定GPS表现不佳的地区。对于每个地区，我们都准备了一个环境包，其中只包含该地区的道路网络和建筑调查数据。与城市规模的道路网络和建筑调查数据相比，这样的地区级环境包将小得多，对智能手机也很友好。因此，用户可以下载他们所需要的软件包。然而，需要付出更多的努力来减少计算开销。

系统弹性和更新。即使城市环境发生变化，例如建造新建筑和/或拆除旧建筑，DeepGPS仍然有效。这是因为我们的深度神经网络模型捕捉到了GPS估计和定位上下文之间的一般映射关系。一旦城市环境变化被记录在道路网络文件或建筑测量数据中，这样的信息就可以立即被编码在环境矩阵中。此外，我们提出了约束掩码$C_{env}$，它嵌入了周围环境（如建筑物）的先验知识，以约束正确位置的预测。因此，如果某个区域被新建筑占用，则在约束掩码$C_{env}$中，这些建筑覆盖的单元将标记为不可用。有了这些设计，我们的系统可以有效地校正GPS估计，从而对环境变化具有弹性。

尽管有上述新颖的设计，我们仍然建议使用最新的资源数据定期重新训练模型，包括新收集的GPS样本、最新的道路网络和建筑测量数据。周期性的模型再训练旨在及时更新GPS估计与定位上下文之间的映射关系。具体来说，在给定的一段时间后，例如三个月，我们可以使用最新的资源数据重新训练模型。一般来说，再培训过程可以在几个小时内完成。例如，为中国深圳市训练模型大约需要6.6个小时。在模型再训练过程中，现有模型仍然可以用于服务定位请求。一旦完成模型再培训，我们将用更新的模型取代旧模型，以提供更准确的定位服务。

再现性数据发布。我们分享了DeepGPS实现的源代码和真实的现场GPS样本[8]，供社区复制我们的结果并启发未来的研究。

8 CONCLUSION

本文提出了DeepGPS，其利用编码器-解码器网络模型预测每一个错误的 GPS 估计的正确位置。更具体地说，DeepGPS融合了影响城市峡谷 GPS 精度的多个因素（建筑高度、道路分布、时间以及GPS卫星状态），并通过两个并行解码器以预测定位误差和正确的定位位置。我们通过过滤掉不可访问的候选位置，通过一种新颖的约束掩模设计进一步增强了DeepGPS，并使用一种简单而有效的移动模型实现了连续定位。该系统已得到实施和评估。基于大规模公交车轨迹数据集和现场GPS测量的大量实验表明，DeepGPS可以显著增强城市峡谷中的GPS定位，例如，平均有效校正90.1%的GPS估计，精度提高64.6%。