您现在的位置是：首页 >学无止境 >基本的排序算法网站首页学无止境
基本的排序算法
一、插入排序
基本思想：在待排序的元素中，假设前面n-1(其中n>=2)个数已经是排好顺序的，现将第n个数插到前面已经排好的序列中，然后找到合适自己的位置，使得插入第n个数的这个序列也是排好顺序的。按照此法对所有元素进行插入，直到整个序列排为有序。
如下图
代码如下
void StraightSort(int arr[], int n)//排列成升序
{
for (int i = 1; i < n; i++)//直接从第二个元素开始排序，因为一个元素一定有序
{
int tmp = arr[i];//记录要排序的元素
int j = 0;
for (j = i - 1; j >= 0 && arr[j] > tmp; j--)//将大于tmp的元素后移
{
arr[j + 1] = arr[j];
}
arr[j + 1] = tmp;//将空出来的位置填上要排序的元素
}
}时间复杂度是O(n^2),空间复杂度O(1)
时间复杂度是否可以优化？
我们在前面有序序列中找元素的位置时，其实可以用二分法进行查找优化，这样时间复杂度可以变为O(nlogn)
代码如下
void BinsertSort(int arr[], int n)
{
for (int i = 1; i < n; i++)
{
int tmp = arr[i];
int low = 0, high = i - 1;
while (low <= high)
{
int mid = low + (high - low) / 2;
if (arr[mid] <= tmp)
low = mid + 1;
else
high = mid - 1;
}
//二分查找完成之后,low前面的元素全部<=tmp(不包含low),high后面的元素全部>tmp(不包含high)
for (int j = i; j > low; j--)//将大于tmp的元素全部往后移
arr[j] = arr[j - 1];
arr[low] = tmp;
}
}这里介绍另外一个算法---希尔排序
算法思想：将相隔为 d (d=n/2) 的元素进行插入排序，然后d=d/2在进行插入排序，直到d=1。这样咋一看好像和之前的排序没啥区别，甚至更加繁琐，但本质是为了让原本无序的数组在一定范围内变得相对有序，这样移动元素时会减少移动的次数，从而减少时间复杂度，所以它的时间复杂度其实和数组的无序程度有关，数组越无序，时间复杂度越低，数组越有序，时间复杂度越高，在n^1.3~n^2之间
代码如下
void Shellsort(int arr[], int n)
{
for (int d = n / 2; d >= 1; d /= 2)
{
//这里的排序要好好琢磨一下，是按照顺序每次将tmp和与它相隔d的倍数的元素进行排序
for (int i = d + 1; i < n; i++)
{
int tmp = arr[i], j = 0;
for (j = i - d; j >= 0 && tmp < arr[j]; j -= d)
arr[j + d] = arr[j];
arr[j + d] = tmp;
}
}
}二、交换排序
基本思想：初始状态时，将有序序列看作空序列，并将所有记录作为无序序列。比较无序序列的两个待排序的关键字，若为逆序则相互交换位置，否则保持原来的位置不变
主要有两种算法：冒泡排序和快速排序
1.冒泡排序---时间复杂度O(n^2)，空间复杂度O(1)
相信大家都会，这里就不做过多介绍，直接上代码
//冒泡排序
void BubbleSort(int arr[], int n)
{
for (int i = 0; i < n - 1; i++)//要排序n-1趟
{
for (int j = 0; j < n - 1 - i; j++)//每次要比较n-1-i对元素
{
if (arr[j] > arr[j + 1])
{
int t = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = t;
}
}
}
}时间复杂度O(n^2),空间复杂度O(1)
2.快速排序---平均时间复杂度O(nlogn)
这个算法敢叫快速排序，就已经可以看出它的不同寻常，下面我们就来见识一下
基本思想：当我们排序一个无序数组时，我们可以先确定一个元素的位置，让它的左边全是小于等于它的元素，右边全是大于等于它的元素，然后分别在它的左边和右边进行相同的操作，直至数组有序，很显然这是一个分而治之的思想，即将一个问题化简成几个与它相似的子问题，一般是用递归来实现，代码的实现不是很复杂，先实现代码，然后再讲为啥它快速
int partiton(int arr[],int low,int high)
{
int tmp=arr[low];//假设我们找[low,high]中第一个元素的位置
while(low<high)//当low==high时,说明没有可以排序的数据，结束循环
{
while(low<high&&arr[high]>=tmp)high--;
arr[low]=arr[high];
while(low<high&&arr[low]<=tmp)low++;
arr[high]=arr[low];
}
arr[low]=tmp;
return low;
}
void QuickSort(int arr[],int low,int high)
{
if(low<high)//中间没有元素，说明该元素位置是固定的，不用在排序了
{
int povit=partiton(arr,low,high);//先确定一个元素的位置
QuickSort(arr,low,povit-1);//在排序它的左边
QuickSort(arr,povit+1,high);//在排序它的右边
}
}
注意上面的递归过程不是函数的递归顺序，而是方便我们理解递归过程的逻辑化的示意图，本质递归会先将左边的数据排序后，才会排序右边的数据，这里我们左右同时开工，是为了更好的理解它的算法思想和时间复杂度问题。
根据上面的递归过程示意图我们就能大致能感受到它的时间复杂度很低，每一层的遍历个数都小于O(n),所以时间复杂度跟递归层数有关为O(n*递归层数)，而递归层数如下图
显然递归层数与二叉树的深度有关，而二叉树的深度其实和选中要确定的数据大小有关，如果每次选中的数据都在区间的中间位置，那么二叉树深度会减少，而每次选中的数据都在偏前或偏后的位置，二叉树的深度会增加(有点类似于平衡二叉树) ，但是平均来说算法的时间复杂度是O(nlogn) ,而空间复杂度就是看递归的深度，即二插树的深度，平均为O(nlogn)
三、选择排序
基本思想：对n个待排序的记录进行n-1趟扫描，第i趟扫描将从无序序列中选出最小关键字值的记录，并将其与第i个记录交换
如下图
代码如下
//选择排序
void SimpleSelectSort(int arr[], int n)
{
for (int i = 0; i < n - 1; i++)//只要比较n-1次，就能排好序
{
//假设i是最小元素的下标，这里记录最小元素的下标，这样元素的只要交换一次
int index = i;
for (int j = i + 1; j < n; j++)
{
//找到最小元素的下标
if (arr[index] > arr[j])
index = j;
}
//将它移到最前面
int tmp = arr[i];
arr[i] = arr[index];
arr[index] = tmp;
}
}时间复杂度O(n^2),空间复杂度O(1)
其实选择排序本质上就是在找数组中的最大值或最小值，然后进行交换，这里再介绍一种方法
堆排序---时间复杂度是O(nlogn)
基本思想：堆这种结构分为大根堆和小根堆，它的堆顶元素要么是最大值(大根堆)，要么是最小值(小根堆),所以我们只要利用这个性质，不断的创建堆，得到堆顶元素，就能得到有序的数组
-
堆中某个结点的值总是不大于或不小于其父结点的值
-
堆总是一棵完全二叉树
这里简单说一下堆的结构（以小根堆为例）
代码如下
//堆排序---大根堆
void Adjust(int arr[], int parent, int len)//parent代表哪个堆要调整
{
for (int i = 2 * parent + 1; i < len; parent = i,i = i * 2 + 1)
{
if (i + 1 < len && arr[i + 1] > arr[i])//比较左右孩子的大小
i++;
if (arr[parent] > arr[i])//比较堆顶元素和较大孩子的大小，如果大于则说明位置正确
break;
else//如果不大于，则让最大元素做堆顶，在从子树中找该元素位置
{
int tmp = arr[parent];
arr[parent] = arr[i];
arr[i] = tmp;
}
}
}
void HeapSort(int arr[], int n)
{
//将数组变成大根堆
for (int i = n / 2 - 1; i >= 0; i--)
Adjust(arr, i, n);
for (int i = n - 1; i > 0; i--)
{
//交换堆顶元素
int tmp = arr[0];
arr[0] = arr[i];
arr[i] = tmp;
//调整数组，使得它再次成为堆
Adjust(arr, 0, i);
}
}这里讲一下Adjust函数的实现思想：首先，堆的结构是一个递归的结构，堆的左子树和右子树可以看成是另外两个堆，而Adjust的应用场景是二叉树的左右子树都满足堆的定义时，我们调整堆顶的元素，让整个二叉树都满足堆的定义成为堆，那么一个元素肯定是满足堆的定义的，即叶子结点一定满足堆的定义，我们只要从最后一个非叶子结点开始调整就能得到一个堆，最后一个非叶子节点的下标是n/2-1(可以自行带几个值验证一下，n是元素个数)---这是HeapSort中第一个for循环的思路
那么我们如何对堆顶元素和左右堆进行调整，得到真正的堆呢？
首先我们要找到孩子子树中的最大值（也就是孩子结点中的较大值，因为堆的定义是堆顶元素最大），如果堆顶的元素大于孩子节点中的最大值，那么符合定义，直接跳出循环，如果小于，那么就将它们交换，然后调整以该孩子节点所在的堆，直到找到该元素所在的位置，其实就是元素不断下坠的过程
四、归并排序
基本思想：将两个有序的序列合并成一个有序的序列
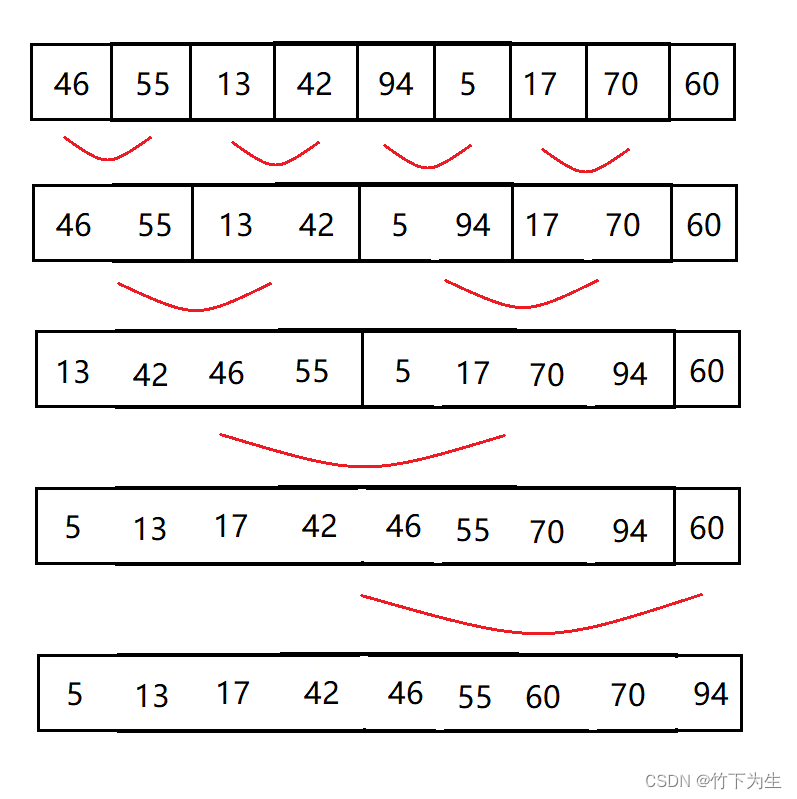
递归实现
//归并排序
void Merge(int arr[], int low, int mid, int high)//[low,mid]和[mid+1,high]两个区间
{
//int num[high-low+1];//如果编辑器支持变长数组，也可以这么写
int num[100] = { 0 };//这里的数组大小根据需求变化
int i = low, j = mid + 1, k = 0;
while (i <= mid && j <= high)
{
if (arr[i] < arr[j])
num[k++] = arr[i++];
else
num[k++] = arr[j++];
}
while (i <= mid)num[k++] = arr[i++];
while (j <= high)num[k++] = arr[j++];
memcpy(arr + low, num, sizeof(int) * k);
}
void MergeSort(int arr[], int low, int high)//[low,high]
{
if (low < high)
{
//注意当mid = low + (high - low + 1) / 2，则只能将数组拆分成(low,mid-1)和(mid,high)
//理由同下
//注意当mid = low + (high - low) / 2，则只能将数组拆分成(low,mid)和(mid+1,high)
//如果数组被分为(low,mid-1)和(mid,high)
//那么当mid和high相差1时，mid==low，而后进行的下一个递归是(mid,high)<=>(low,high)
//也就是当前进来的递归参数，然后就会进入死循环=>第二个递归出现问题
//那么我们只要避免low==mid时，第二个递归的参数和当前所在递归参数相同就行，所以选择(mid+1,high)
int mid = low + (high - low) / 2;
MergeSort(arr, low, mid);//将左边的排好序
MergeSort(arr, mid + 1, high);//将右边的排好序
Merge(arr, low, mid ,high);//最后合并
}
}迭代法
void Merge(int arr[], int low, int mid, int high)//[low,mid]和[mid+1,high]两个区间
{
//int num[high-low+1];
int num[100] = { 0 };
int i = low, j = mid + 1, k = 0;
while (i <= mid && j <= high)
{
if (arr[i] < arr[j])
num[k++] = arr[i++];
else
num[k++] = arr[j++];
}
while (i <= mid)num[k++] = arr[i++];
while (j <= high)num[k++] = arr[j++];
memcpy(arr + low, num, sizeof(int) * k);
}
void MergeSort(int arr[], int n)
{
for (int sub = 1; sub < n; sub *= 2)
{
int first = 0, last;
while (first + sub < n)
{
last = first + 2 * sub - 1;
if (last > n - 1)
last = n - 1;
Merge(arr, first, first + sub - 1, last);
first = last + 1;
}
}
}五、基数排序
基数排序是基于权重大小来进行排序的一种算法，在整数排序时，可以使用，算法的思想就是先比较个位数得到排列顺序，再比较十位数得到新的排序顺序(注意该次排序以十位数为主，如果十位数相同，则会由之前个位数的排序顺序决定)，一直到最高位。
如下图
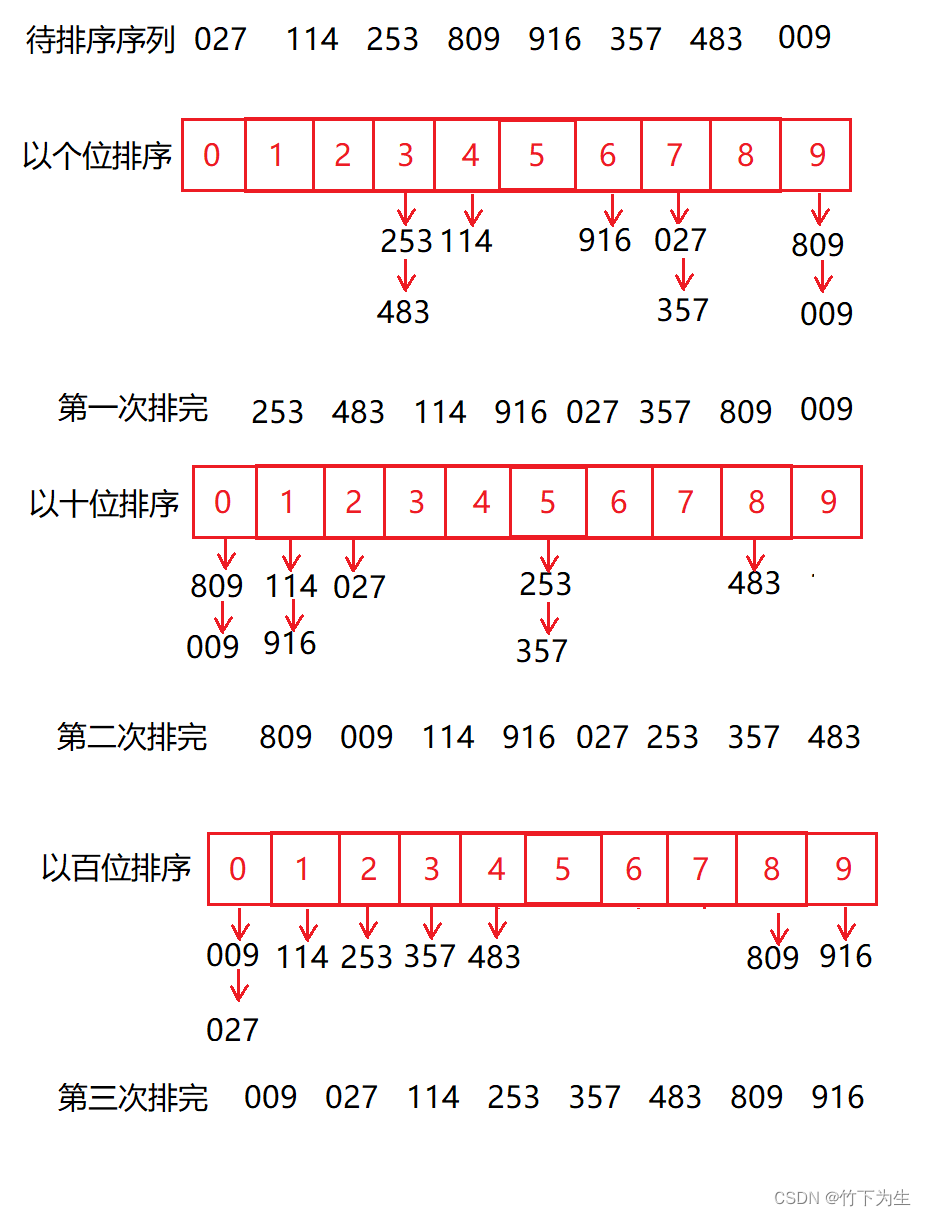
代码如下
//基数排序
void RadixSort(int arr[], int n)
{
int max = INT_MIN;
for (int i = 0; i < n; i++)
max = fmax(max, arr[i]);
int exp = 1;
while (max >= exp)
{
int cnt[10] = { 0 };
for (int i = 0; i < n; i++)
{
int digit = (arr[i] / exp) % 10;
cnt[digit]++;
}
//计算每个数存在的区间，如27这个数，以7这个十位排序时，就将前面0~7的个数相加，得到挂在7下面的元素的最后一个数的位次
for (int i = 1; i < 10; i++)
{
cnt[i] += cnt[i - 1];
}
//int buf[n];//如果编辑器支持可变数组，可以写
int buf[100];//根据数据的个数进行调整
//注意这里必须要从后往前遍历，不然会不满足拿出来的顺序，因为我们是倒着拿出来的
for (int i = n - 1; i >= 0; i--)
{
int digit = (arr[i] / exp) % 10;
buf[cnt[digit] - 1] = arr[i];
cnt[digit]--;
}
memcpy(arr, buf, sizeof(int) * n);
exp *= 10;
}
}基数排序的代码比较难理解，可以多画画图，多理解理解
如果你觉得这篇博客对你有所帮助的话，请不要忘记点赞和评论哦！！！！！！！！
站长推荐
- U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 - stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程） - SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权 - 【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》 - 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效)