您现在的位置是：首页 >其他 >【C++】如何克服红黑树的恐惧？看这篇文章足够了网站首页其他
【C++】如何克服红黑树的恐惧？看这篇文章足够了
红黑树的实现会比AVL简单-.-
判断是否是AVL树
上一篇文章我们详细介绍了AVL树并且实现了AVL树，这篇文章我们将在前言中引入判断是否是AVL树的方法，然后我们就进入红黑树的实现，如果是能自己实现AVL树的同学那么实现起红黑树就会非常简单了，下面我们介绍一下如何判断AVL树：
首先AVL树本质是根据平衡因子的调节来实现平衡，所以我们可以根据平衡因子来判断，代码如下：
bool IsBalance()
{
return _IsBalance(_root);
}int _Height(Node* root)
{
if (root == nullptr)
{
return 0;
}
return _Height(root->_left) > _Height(root->_right) ? _Height(root->_left) + 1 : _Height(root->_right) + 1;
}bool _IsBalance(Node* root)
{
if (root == nullptr)
{
return true;
}
int left = _Height(root->_left);
int right = _Height(root->_right);
if (abs(right - left) >= 2)
{
cout << root->_kv.first << "节点的高度差大于等于2" << endl;
return false;
}
if (right - left != root->_bf)
{
cout << root->_kv.first << "节点的平衡因子错误" << endl;
return false;
}
return _IsBalance(root->_left) && _IsBalance(root->_right);
}如上代码所示，我们先写了一个求树高度的函数，因为等会要判断每个节点的左右高度差，然后我们先求出整棵树的左右子树的高度，然后判断左右子树高度差是否小于2，如果不小于则说明不是AVL树，然后再判断平衡因子，平衡因子是等于右子树高度减去左子树高度，如果右树高度减去左树高度不等于平衡因子大小则说明平衡因子错了也不是AVL树，然后我们再分别判断每颗子树即可。下面我们跑一下测试：
void test1()
{
/*int a[] = { 16,3,7,11,9,26,18,14,15 };*/
int a[] = { 4,2,6,1,3,5,15,7,16,14 };
AVLTree::AVLTree<int, int> at;
for (auto& e : a)
{
//打条件断点
/*if (e == 14)
{
int x = 0;
}*/
at.insert(make_pair(e, e));
cout << e << "插入：" << at.IsBalance() << endl;
}
at.Inorder();
cout << endl;
cout << at.IsBalance() << endl;
}
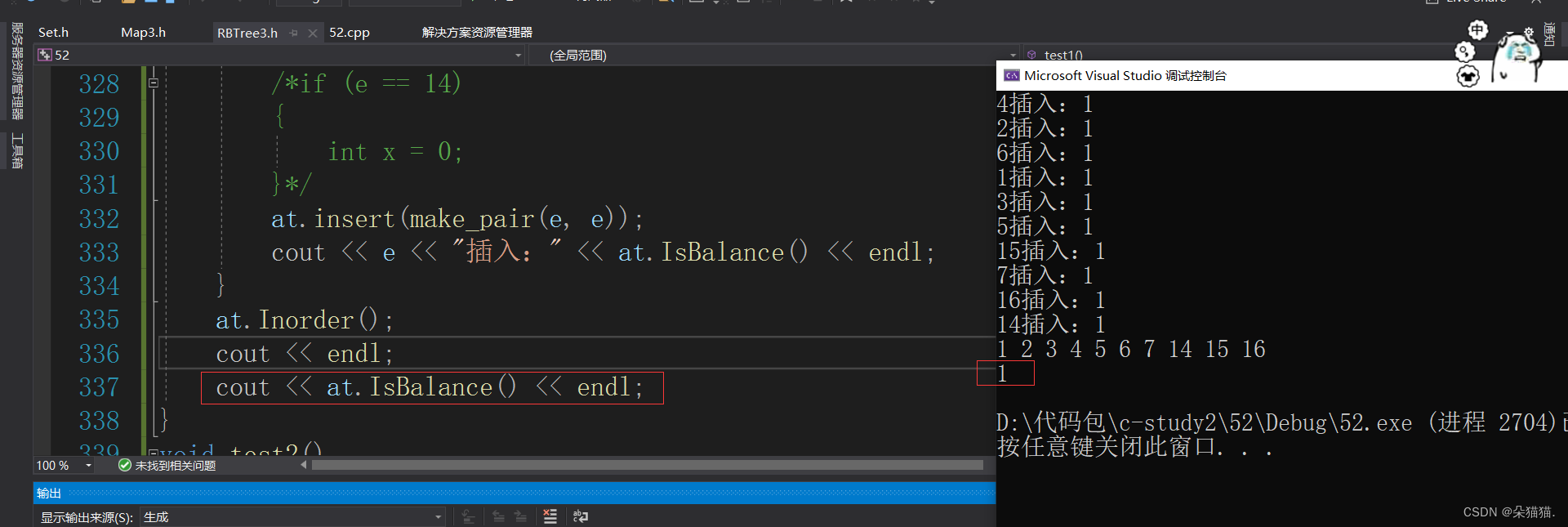
上面条件断点的方式大家可以学一下，当数据量很多需要调试的时候，比如上图中的数据只有插入14的时候才会引发旋转，所以我们可以单独在14这个节点测一下旋转是否正确，只需要写个if语句然后在语句中随便写一个代码，因为如果语句为空是打不上断点的，如下图：
下面在跑一下随机数测试：
void test2()
{
srand(time(0));
const size_t N = 100000;
AVLTree::AVLTree<int, int> at;
for (size_t i = 0; i < N; i++)
{
size_t x = rand();
at.insert(make_pair(x, x));
}
cout << at.IsBalance() << endl;
}
可以看到也是没有问题的，以上AVL树就结束了，下面我们就开始红黑树的学习。
一、红黑树
红黑树的性质：
1. 每个结点不是红色就是黑色。
2. 根节点是黑色的。
二、红黑树的实现
红黑树与AVL数有很多相似的地方，所以我们直接实现红黑树不同的地方即可：
首先我们先将节点写出来：
#include <assert.h>
#include <iostream>
using namespace std;
enum Colour
{
RED,
BLACK
};
template <class K,class V>
struct RBTreeNode
{
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
pair<K, V> _kv;
Colour _col;
RBTreeNode(const pair<K, V>& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_col(RED)
{
}
};与AVL树不同的是红黑树多了一个颜色，所以我们用一个枚举来控制颜色，下面我们先将红黑树插入与AVL树插入差不多相同的地方写好：
template <class K,class V>
class RBTree
{
typedef RBTreeNode<K, V> Node;
public:
bool insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
//根节点必须为黑色
_root->_col = BLACK;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//开始红黑树
}
private:
Node* _root = nullptr;
};下面我们分析红黑树的插入：
从上图中我们可以看到，当新增节点的父节点是黑色时，不会违反任何规则，所以当新增节点的父节点是黑色时不用调整直接插入成功了。
如果是上图这样的情况当新增节点的父亲是红色该怎么办呢？我们可以看到这样是会出现两个连续的红色节点的违反了规则3，当出现这样的情况，我们给出的方法是将parent节点和uncle节点改为黑色，然后将grandfather改为红色，如下图：
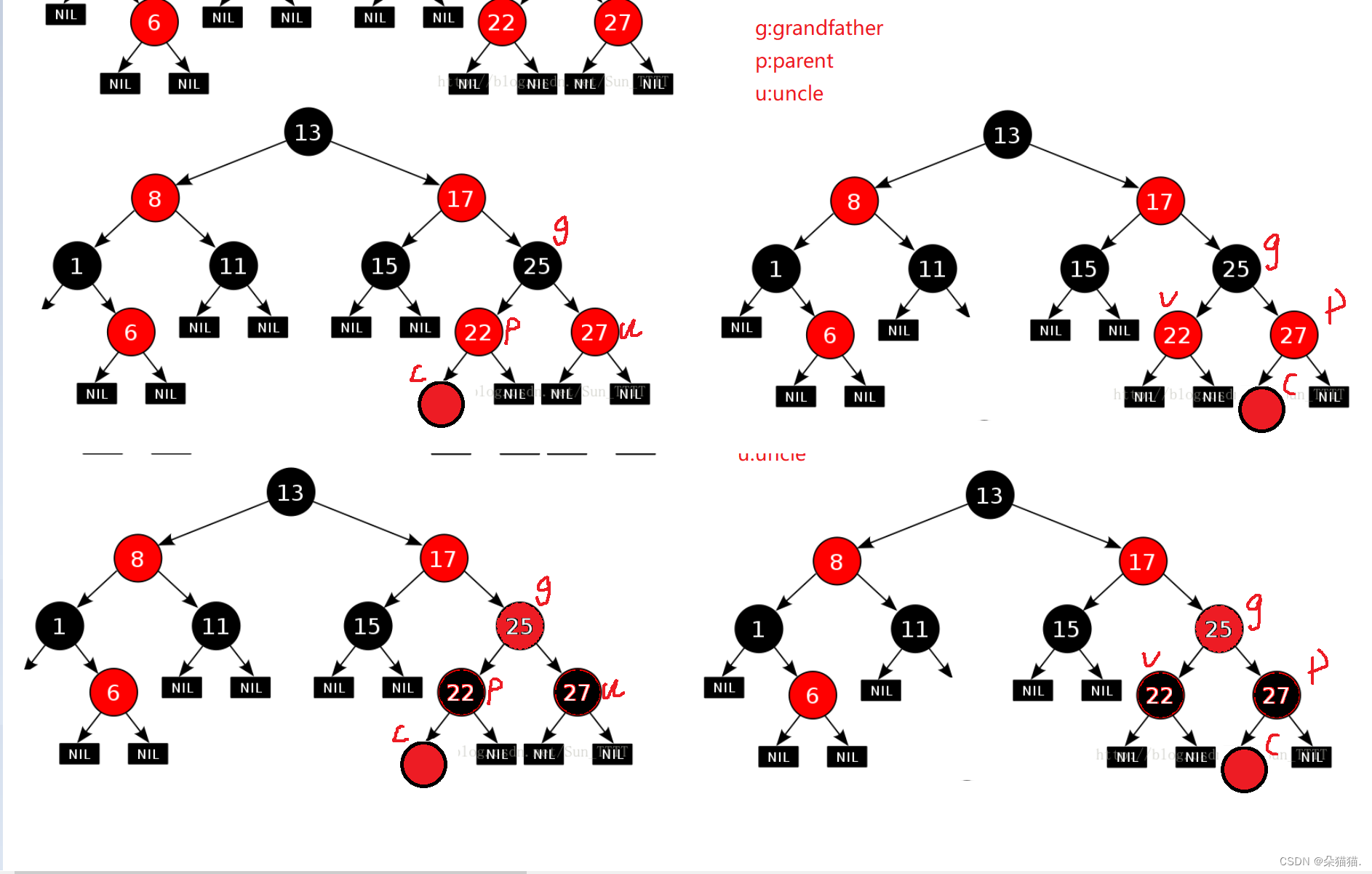
如上图当我们修改完parent,uncle,grandfather的颜色后发现grandfather节点和其父节点也出现了连续的红色，所以这种情况是需要向上调整的，让cur变成grandfather即可：
如上图所示，向上调整完成后如果grandfather是根节点我们还需要将根节点修改为黑色，然后我们发现修改完成后每条路径的黑色节点数量都是相同的并且一个红色节点都有两个黑色节点，下面我们完成代码：
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//开始红黑树
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (parent == grandfather->_left)
{
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)
{
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
//向上调整
cur = grandfather;
parent = cur->_parent;
}
}
}
}这里我们可以看到当parent在祖父的左边那么uncle就是祖父的右边所以要分两种情况，parent在祖父的左边是一种情况，parent在祖父的右边是一种情况。上图我们演示的情况是当叔叔存在并且为红色我们的解决方案，下面看看当叔叔节点不存在或者叔叔节点为黑色的解决方案：
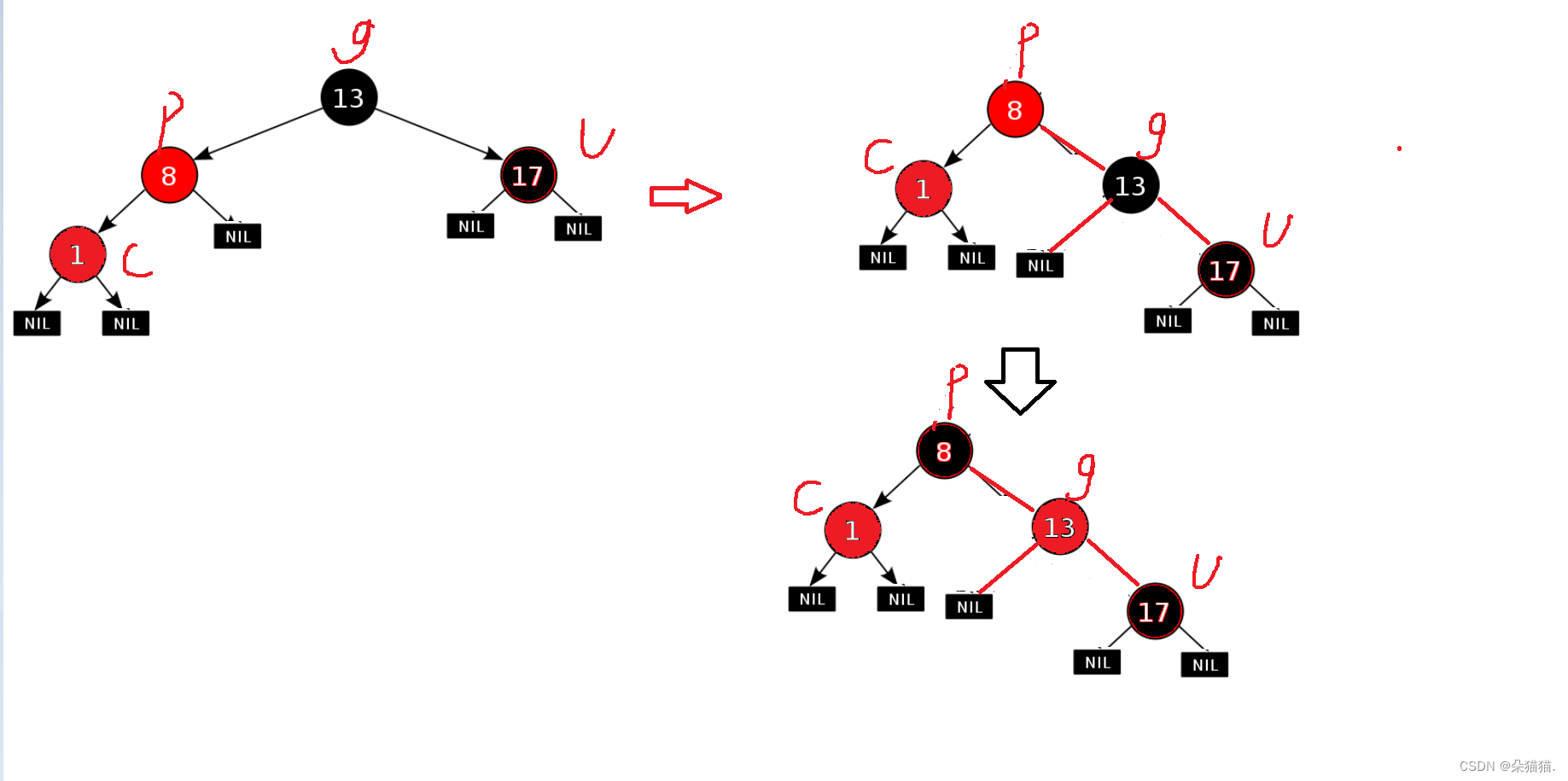
我们可以看到当出现叔叔是黑色的情况是需要旋转的，如果新增节点和parent和grandfather在一条线上的话那就需要先对grandfather节点进行单旋，然后将parent节点变成黑色，grandfather节点变成红色。
这里再次说明：
uncle的情况有两种。1.如果uncle节点不存在，那么cur一定是新插入节点。因为如果cur不是新插入节点，则cur和parent一定有一个黑色节点，就不满足性质4了，就像上图中大家可以把叔叔节点删掉，删掉后发现cur一定是新增节点。
2.如果uncle节点存在，则其一定是黑色的。因为cur节点原先是黑色的，因为新增节点让cur变成了红色。如下图：
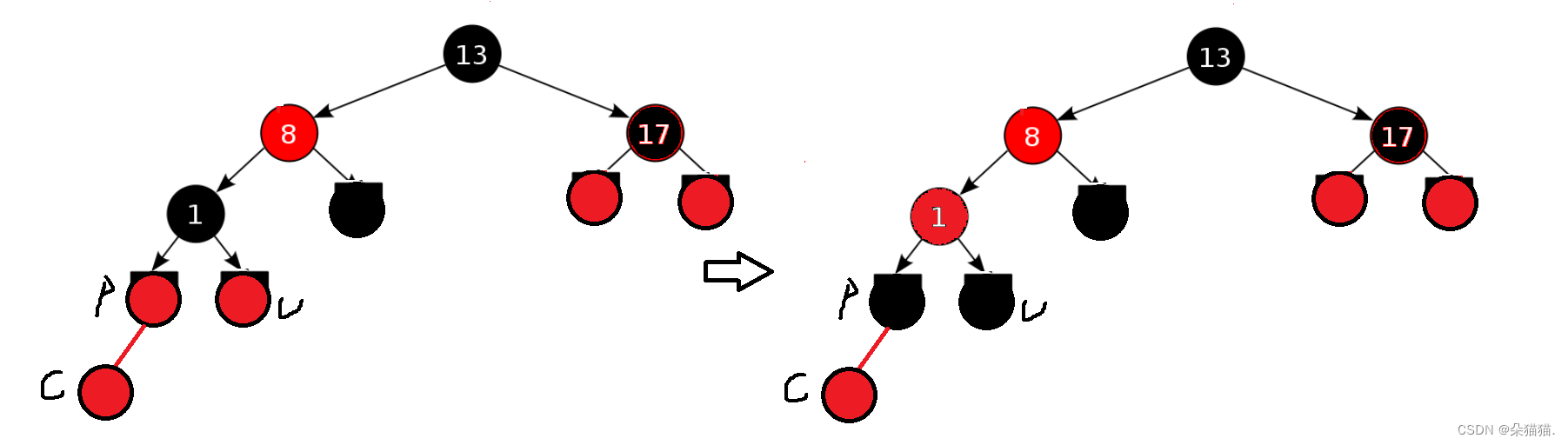
理解了以上知识我们再看看第三种情况：
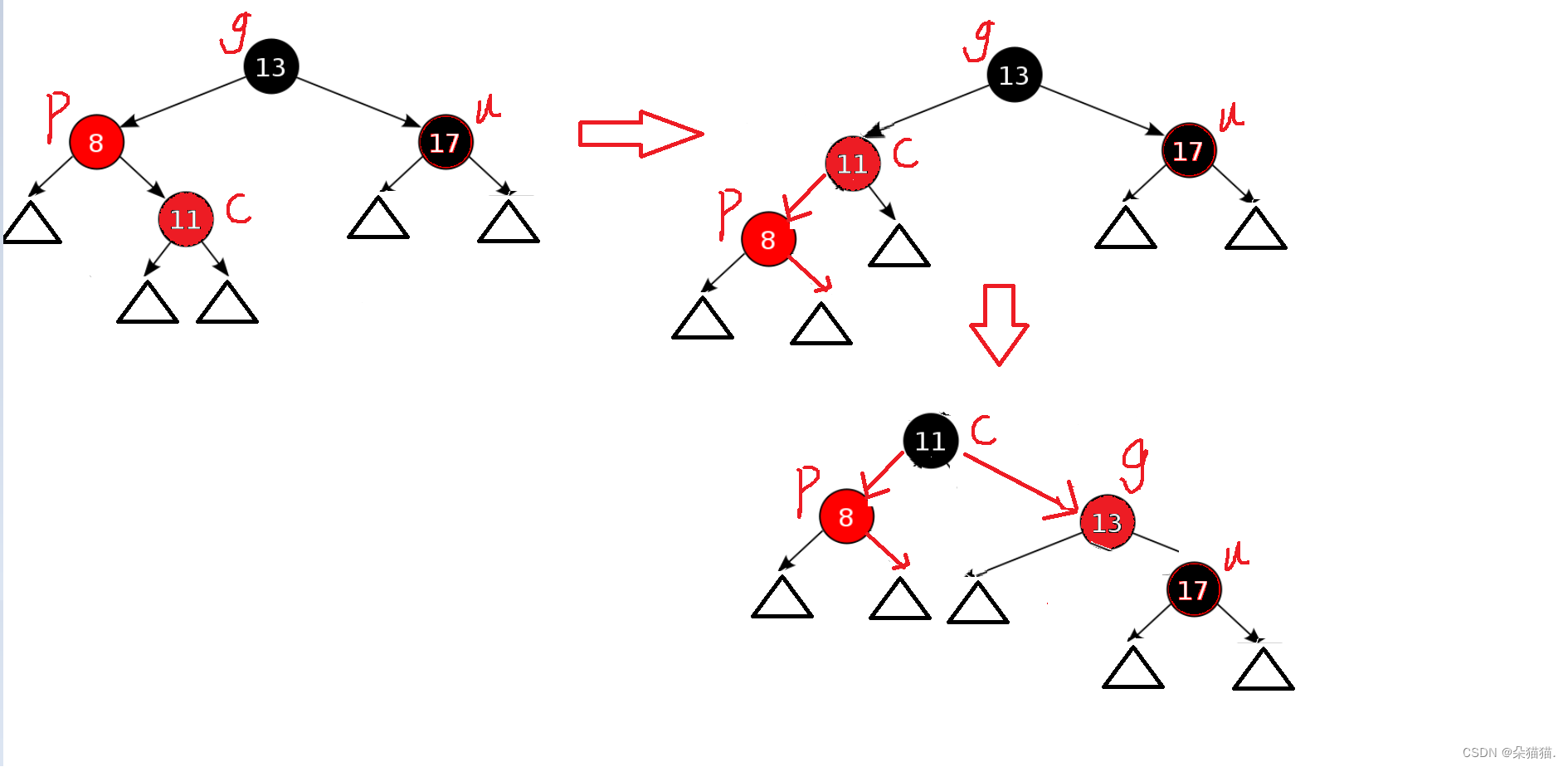
三角形代表多种情况的子树，我们可以看到如果cur和父节点和祖父节点不在一条直线上的时候，这个时候需要双旋，（第一次旋转的是parent，第二次旋转的是grandfather,可以根据图理解）双旋后将cur变成黑色，把parent变成红色，把grandfather变成红色。代码如下：
bool insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
//根节点必须为黑色
_root->_col = BLACK;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//开始红黑树
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (parent == grandfather->_left)
{
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)
{
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
//向上调整
cur = grandfather;
parent = cur->_parent;
}
else
{
// g
// p u
// c
//如上图，u为黑色或不存在，cur与grand和parent在一条直线，先单旋，再变色
if (cur == parent->_left)
{
//右单旋的原因是单纯左边高，结合上图
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
// g
// p u
// c
//当cur在parent的右边祖父节点和父节点和cur是折线形状时，就是双旋
//由于父节点单纯右边高所以先左旋，然后整体高再右旋
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
parent->_col = RED;
grandfather->_col = RED;
}
break;
}
}
else
{
//parent是grandfather->right
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)
{
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
//向上调整
cur = grandfather;
parent = cur->_parent;
}
else
{
// g
// u p
// c
//如上图，u为黑色或不存在，cur与grand和parent在一条直线，先单旋，再变色
if (cur == parent->_right)
{
//左单旋的原因是单纯左边高，结合上图
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
// g
// u p
// c
//当cur在parent的右边祖父节点和父节点和cur是折线形状时，就是双旋
//由于父节点单纯左边高所以先右旋，然后整体高再左旋
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
parent->_col = RED;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return true;
}需要我们注意的是，第一种情况叔叔存在并且为红色，这种情况需要向上调整所以不能break退出循环，但是第二种情况和第二种情况一旦旋转后那么一定是平衡了所以直接break即可，在退出前我们将根节点颜色再次置为黑色，然后返回true即可。下面我们写一个析构函数然后测试代码：
~RBTree()
{
_Destroy(_root);
_root = nullptr;
}
void _Destroy(Node* root)
{
if (root == nullptr)
{
return;
}
_Destroy(root->_left);
_Destroy(root->_right);
delete root;
}注意了，上面我们没有将单旋的代码演示出来是因为单旋和AVL中的实现一模一样只不过没有了平衡因子的修改。
下面我们想想如何判断一颗树是不是红黑树呢？要判断红黑树只需要根据红黑树的几条性质就能判断，代码如下：
bool IsBalance()
{
return _IsBalance(_root);
}
bool _IsBalance(Node* root)
{
if (_root&&_root->_col != BLACK)
{
cout << "根节点的颜色不是黑色" << endl;
return false;
}
int benchMark = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
{
++benchMark;
}
cur = cur->_left;
}
return _Check(root, 0, benchMark);
}
bool _Check(Node* root, int blackNum, int benchMark)
{
if (root == nullptr)
{
if (blackNum != benchMark)
{
cout << "某条路径的黑色节点与其他路径不相等" << endl;
return false;
}
return true;
}
if (root->_col == BLACK)
{
++blackNum;
}
if (root->_col == RED
&& root->_parent
&& root->_parent->_col == RED)
{
cout << "存在连续的红色节点" << endl;
return false;
}
return _Check(root->_left,blackNum,benchMark) && _Check(root->_right,blackNum,benchMark);
}首先我们检查根节点是否存在并且根节点是否是黑色，然后检查每条节点的路径是否相等以及是否有连续红色节点，由于涉及到递归所以我们重新用另一个函数实现，在check函数中，我们的第二个参数是黑色节点数量，第三个参数是一个基准值，这个基准值我们给的是红黑树中最左路径。当递归到空树有两种情况，第一种情况是判断当前这条路径的黑色节点数量是否与基准值相同，如果不相同就返回false，相同就证明这条路径遍历完了返回true即可。每次递归遇到黑色节点就让NUM++，这里是传值传参所以每条路径的黑色节点数量互不影响。然后判断当前节点和其父节点是否都为红色，这里判断父亲的原因是因为简单，如果判断当前节点和孩子节点是否有连续红色节点的话，那么还要分左孩子和右孩子还要空的情况会更复杂。判断父节点之前也先确定父节点是否存在，因为如果是根节点的话父亲为空。然后递归判断每一颗子树即可，下面我们就验证一下：
void test1()
{
int a[] = { 4,2,6,1,3,5,15,7,16,14 };
RBTree<int, int> at;
for (auto& e : a)
{
at.insert(make_pair(e, e));
}
at.Inorder();
cout << endl;
cout << at.IsBalance() << endl;
}
void test2()
{
srand(time(0));
const size_t N = 100000;
RBTree<int, int> rt;
for (size_t i = 0; i < N; i++)
{
size_t x = rand() + i;
rt.insert(make_pair(x, x));
}
cout << rt.IsBalance() << endl;
}
通过多次测试我们发现代码并没有问题，以上就是红黑树的全部内容了。
总结
站长推荐
- U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 - stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程） - SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权 - 【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》 - 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效)