【控制理论】——PID算法网站首页 技术教程

【控制理论】——PID算法

柯宝最帅 2023-05-18 04:00:01

简介【控制理论】——PID算法

前言

前言

声明：学习笔记来自b站421施工队和正点原子电机教程，仅供学习交流！！

一、PID算法

PID 是 Proportional（比例）、Integral（积分）、Differential（微分）的首字母缩写，它是一种结合比例、积分和微分三个环节于一体的闭环控制算法。本质是根据输入的偏差值，按照比例、积分、微分的函数关系进行运算，运算结果用以控制输出。

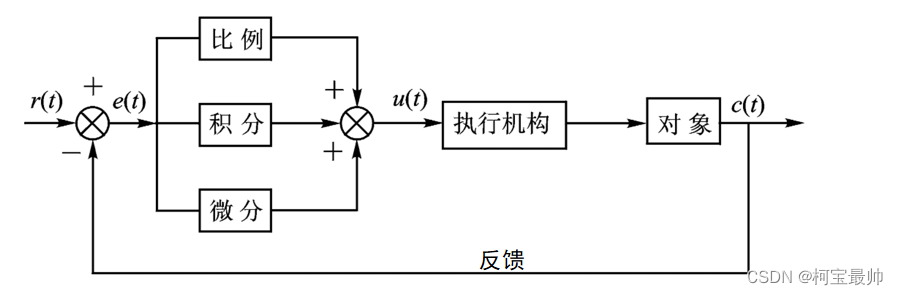
PID算法适用于线性系统（满足叠加性和齐次性）——二阶以内的线性系统。

不适用系统：高阶系统，非线性系统。如果要使用，高阶系统需可以简化为二阶系统，非线性系统要利用李雅普诺夫第一方法在非线性系统的平衡点处线性化。更多可继续研究！

1、控制系统分类&参数&信号

分类：

①开环控制系统（无反馈）：一般开环系统、前反馈控制系统（执行器在对对象作用时补偿了干扰，如下图）

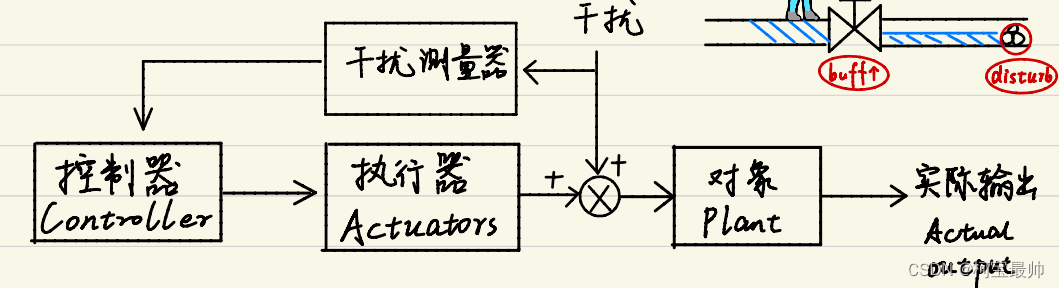
②闭环控制系统（有反馈）：单闭环（输出端有反馈）、双闭环（不仅输出端有反馈，中间副对象也有反馈，如下图双环）

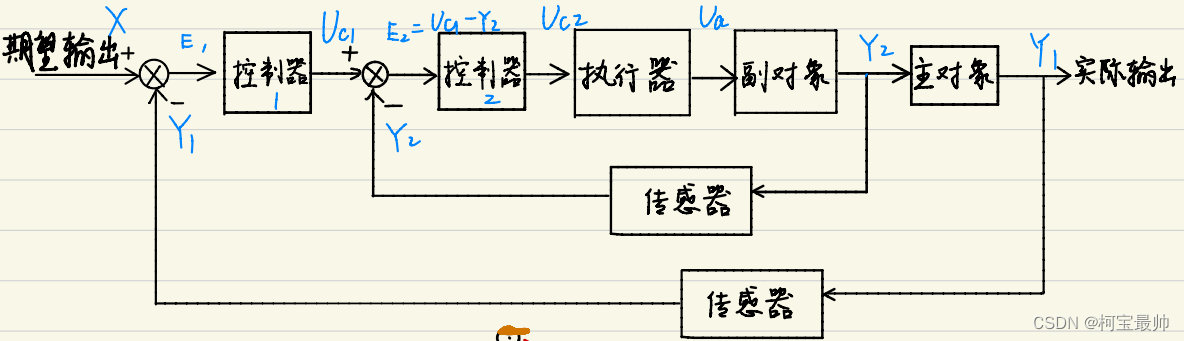
③复合控制系统（全称前馈反馈复合控制系统）

参数：

误差（e） = 期望输出（输入）- 实际输出

控制器输出（C）：给执行器的信号

执行器输出：被作用对象（如阀门）的变化

系统输出Y：实际输出（如水流量变化）

信号：

连续与离散信号：采样保持器获取该时刻的电压信号保持一个采样周期，也就是红色横线对应的时间

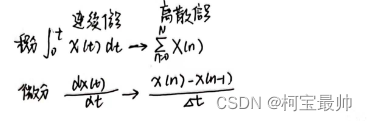
2、PID算法简介

三个环节：

比例环节：成比例地反应控制系统的偏差信号，即输出C与输入偏差e成正比，可以用来减小系统的偏差。

结论：K_p越大，系统响应越快，越快达到目标值；K_p过大会使系统产生较大的超调和振荡，导致系统的稳定性变差；有比例环节无法消除静态误差。

静态误差：系统控制过程趋于稳定时，目标值与实测值之间的偏差。产生原因：输出被外部影响抵消。可通过引入积分环节消除静态误差。

积分环节：对输入偏差e进行积分，只要存在偏差，积分环节就会不断起作用，主要用于消除静态误差。

结论： K_i越大，消除静态误差的时间越短，越快达到目标值；K_i过大会使系统产生较大的超调和振荡，导致系统的稳定性变差；对于惯性较大的系统，积分环节动态响应较差，容易产生超调、振荡。

微分环节：反应偏差量的变化趋势，根据偏差的变化量提前作出相应控制，减小超调，克服振荡。

结论：K_d或者变化趋势越大，微分环节作用越强，对超调和振荡的抑制越强； K_d过大会引起系统的不稳定，容易引入高频噪声。

公式：

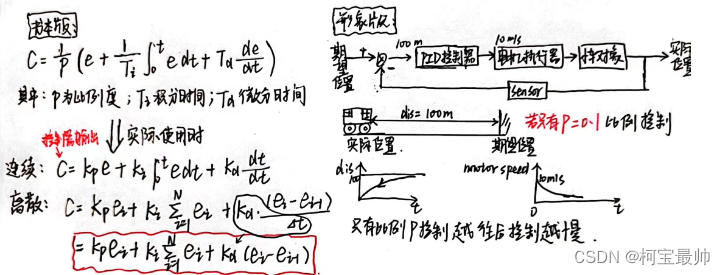
其实公式分位置式和增量式两种（正点原子控制器输出用uk表示，对应上式C）

①位置式

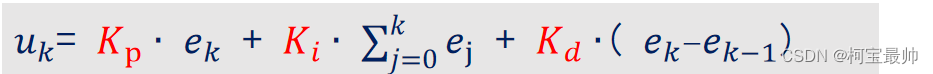
特点： uk直接对应对象的输出（位置），如果计算出现异常，对系统影响很大；全量计算（前面的量都要完全参与到输出的计算中），要对偏差 e 进行累加，计算量大；在不带积分部件的对象中可以得到很好效果，例如电液伺服阀、温控设备等。

②增量式

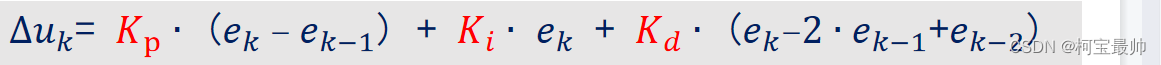
特点：增量式PID计算的是相对上一次输出的增量，即u_k= u_k−1+ ∆u_k ；增量只与近3次的偏差有关，计算出现异常对系统工作影响较小；计算量少，实时性相对较好。

举例理解：

无人机例子与小车的不同在于，小车只有比例控制P时到最后虽然变化慢但只要有一点速度（不等于0）就会接近期望位置，但无人机则不同，因为它还要克服自身重力，（只有比例p控制时）当速度小到某一值（悬浮速度）时，无人机会一直在这一位置悬停无法再往期望位置靠近，只能接近不可到达准确位置。即单个P项比例控制不可消除稳态误差，这时需要积分控制I，如果误差e一直不变（悬停），就可使积分项积累，增大了控制量，积分项的指不会因为当前误差e的值等于0而变化，只会停止积累。而微分控制D则主要用来抵消调节过度（正常来说误差e是不断减小的，当调节过度就会导致超调，误差变大），这时微分项会变为负值抵消过度的调节。

PID结构体定义&函数实现：

typedef struct
{
    __IO float  SetPoint; 			/* 目标值 */ 
    __IO float  ActualValue;     	/* 期望值 */
    __IO float  SumError;            	/* 偏差累计 */
    __IO float  Proportion;          	/* 比例常数 P */
    __IO float  Integral;            	/* 积分常数 I */
    __IO float  Derivative;          	/* 微分常数 D */
    __IO float  Error;               		/* Error[1] */
    __IO float  LastError;           	/* Error[-1] */
    __IO float  PrevError;           	/* Error[-2] */
} PID_TypeDef;

PID初始化函数：初始化PID的相关参数（清零），设置PID系数

PID闭环控制函数：实现位置、增量式PID控制算法

TIM6更新中断函数：调用PID闭环控制函数，计算后返回输出（期望值）。即控制PWM输出

PID上位机调试函数：实现上位机和开发板之间的通讯，进行PID调参。

二、PID参数整定

采样周期：采样周期指的是PID控制中实际值的采样时间间隔，其越短，效果越趋于连续，但对硬件资源的占用也越高。怎么选择？理论上可根据香农采样定理；实际应用中，根据实际值突变能力选择采样周期。

PID参数整定方法很多总结来说有两类。理论计算整定（数学模型）、工程整定法（试凑法、临界比例法、一般调节法）。但无论哪种方法，最后应用时都要根据经验和实际情况进行调整：

系统振荡

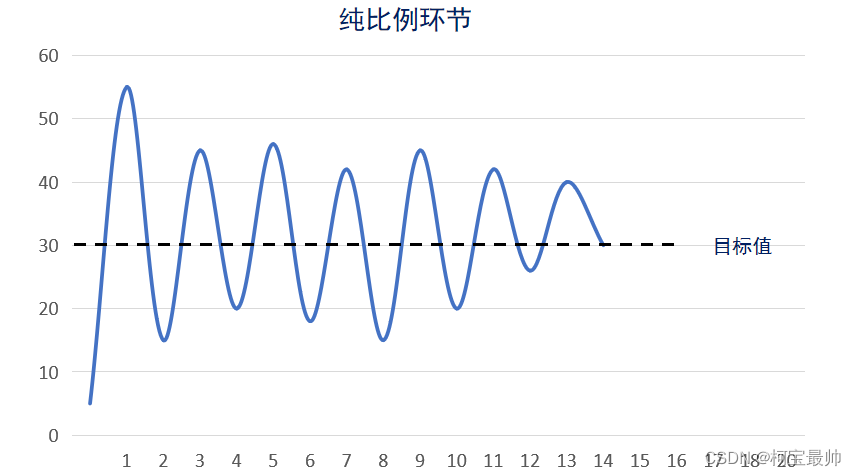
振荡太大，可减小比例系数，减少振荡；振荡减小了很多后，但开始存在超调，再加入微分环节调节，消除初始振荡超调

静态误差

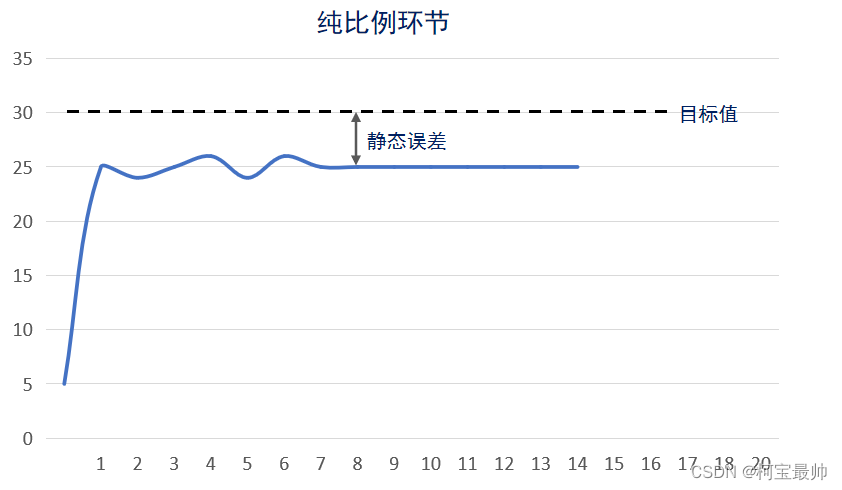
存在静态误差，可引入积分环节（或增大积分系数），可达目标值。如果还嫌消除静态误差的时间太长，可继续增大积分系数。

超调

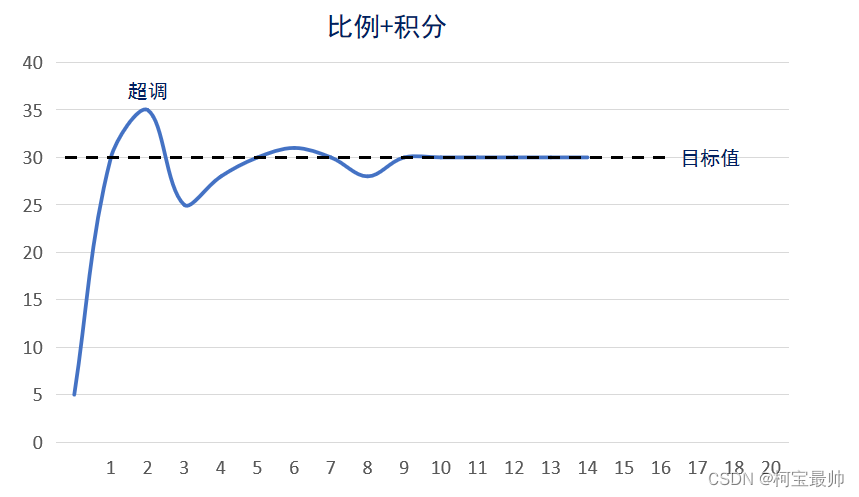
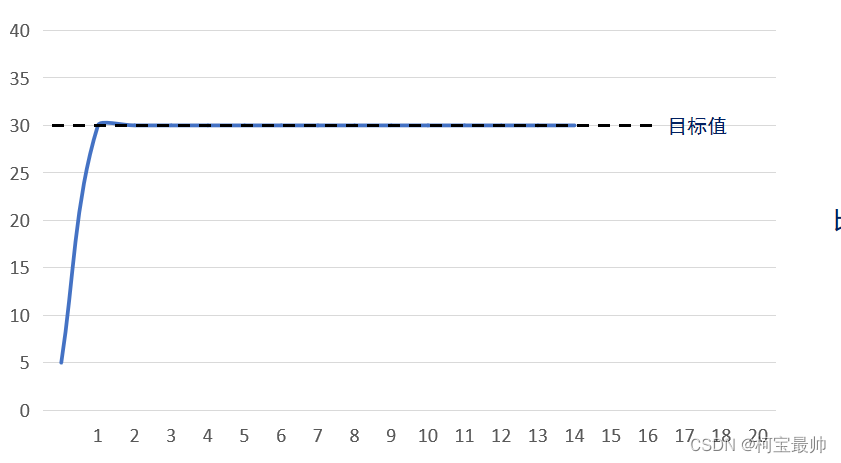
存在较大超调，可减小积分系数、增大微分系数来调节，如右图。

三、PID上位机通信协议

1、数据帧&协议调试

PID调试助手收发数据均按照以下格式（当然这是正点原子的）：

数据类别即数据属性，速度、温度等；数据域即具体的值；校验和采用 CRC16-MODBUS校验，校验范围包括帧头、数据类别和数据域。

利用串口调试助手模拟开发板，和PID调试助手进行通讯。需要准备USB转TTL模块（硬件）、PID调试助手和串口调试助手（软件）、PID调试助手通讯协议（文件）。

这是不通用的，协议是一种规定，只不过这里按照的是正点原子的规定！

......

......等待自己实践！

2、协议代码实现

以下都是实现思路，等待自己实践时继续更新......

协议的数据类别和某些数据域都有固定的数据帧，用枚举类型来管理更加方便：

底层代码实现思路：

①串口1初始化函数：初始化串口1，开启中端接收，用于上位机通讯

②内存初始化函数：在指定地址初始化一段内存（清零）

③CRC16校验函数：对帧头、数据类别、数据域进行校验

④上位机数据解析函数：解析上位机下发的数据，存进指定的结构体中

⑤数据上传函数：上传指定的数据到上位机

应用层代码实现思路：

①初始化调试函数：条用内存初始化底层函数，初始化所需内容

②PID数据上传函数：上传PID参数，设置PID目标值数据同步

③一系列数据上传函数：调用底层数据上传函数，上传电流值、电压值等

④PID参数接收函数：接受上位机设置的PID参数值

⑤命令接收函数：接受上位机下发的指令，例如电机运行、刹车等

⑥速度范围设置函数：限制电机目标速度的范围以及速度的最大突变值

更多相关知识在电机系列，直流有刷电机！

拓展：

拓展来自421施工队，自己理解不是很透彻的部分，先记录下来！

①积分限幅

想象一个场景，无人机起飞时用手按住——其实积分的作用是误差带来的，误差大，积分作用越强。而且有一直积累的特性，积分积累会非常大，可能烧坏电机或者一松手会以非常大的速度冲出去，所以尽量让无人机自由起飞或者对积分累积的最大值进行限幅（其实就是对Iterm设定最大值限制）。超过设定值Iterm清零。

②积分分离

无人机悬停再目标位置地表100m，误差e=0——此时P项（Pterm）为0，要保持无人机悬停，所以I项（Iterm）不为0，此时误差不再累积，所以I项Ierm值保持不变。此时若突然给无人机一个新的目标值，比如到地表1000m，误差e突然飙升到900m，导致Ierm在一定时间内突变，Pterm也是如此，可能导致系统震荡甚至超调。这时需要积分分离，如设定对于积分项而言最大误差e不可超过500m，一旦超过就使积分项Iterm为0。

③微分先行

上面②的例子，当误差突变的时候，影响会先给P和I项，不会影响D项。

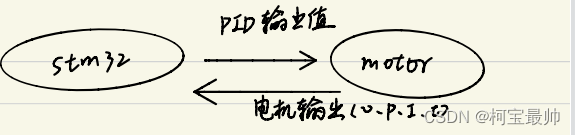
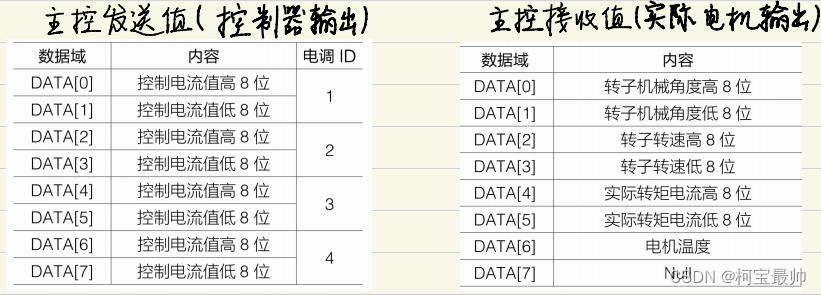
上述值的发送和接收遵循CAN协议！具体看参见这篇文章xxxxx。

1、RM电机M3508速度单闭环（参考系统分类图）

/*位置pid算法*/
void pid_calc(_pid* pid){
	pid->e = pid->target - pid->current;//误差e
	pid->p_out = (int32_t)(pid->Kp * pid->e);//比例项P
	
	//积分隔离
	if (fabs(pid->e) < I_Band){
		pid->i_out += (int32_t)(pid->Ki * pid->e);//积分项I
		limit(&(pid->i_out),pid->IntegralLimit);//积分限幅
	}
	else{
		pid->i_out = 0;
	}
	
	pid->d_out = (int32_t)(pid->Kd * (pid->e - pid->last_e));//微分项D
	pid->total_out = pid->p_out + pid->i_out + pid->d_out;//总控制项
	
	//pid输出限幅
	limit(&(pid->total_out),pid->MaxOutput);
	
	pid->last_e = pid->e;//上一次误差
}

/*速度单环*/
chassis_motor_pid[i].SpeedPID.target = 500;
chassis_motor_pid[i].SpeedPID.current = motor_chassis[i].speed_rpm;
pid_clac(&chassis_motor_pid[i].SpeedPID);//调用PID算法做运算

2、RM电机6020角度双闭环（参考系统分类图）

/*角度双环*/
AnglePID.target = 3.14*30/180;//期望角度30°转换为弧度制
update_angle(&manipulator_motor_pid[i].angle , motor_manipulator[i].angle);//更新电机实时角度，函数定义见下
manipulator_motor_pid[i].AnglePID.current = manipulator_motor_pid[i]._angle.angle;//当前角度
pid_calc(&manipulator_motor_pid[i].AnglePID);//调用PID算法做运算

manipulator_motor_pid[i].SpeedPID.target = manipulator_motor_pid[i].AnglePID.total_out//速度期望（内环），即外环控制器的输出
manipulator_motor_pid[i].SpeedPID.current = motor_manipulator[i].speed_rpm;//当前速度（内环）
pid_calc(&manipulator_motor_pid[i].SpeedPID);//调用PID算法做运算，该函数与单闭环一致


void update_angle(motor_angle* _angle , uint16_t angle_fb){
	_angle->encoder = angle_fb;
	if(_angle->encoder_is_init){
		if(_angle->encoder - _angle->last_encoder > 4096)
			_angle->round_cnt --;
		else if(_angle->encoder - _angle->last_encoder < -4096)
			_angle->round_cnt ++;
	}
	else{
		_angle->encoder_offset = _angle->encoder;
		_angle->encoder_is_init = 1;
	}
	_angle->angle_offset = _angle->angle_offset / 8192.0f * 360.0f;
	_angle->last_encoder = _angle->encoder;
	_angle->total_encoder = _angle->round_cnt * 8192 + _angle->encoder - _angle->encoder_offset;
	_angle->angle = _angle->total_encoder / 8192.0f * 360.0f;
}