您现在的位置是：首页 >技术杂谈 >【数据结构】树，二叉树，满二叉树，完全二叉树的定义和二叉树的基本操作网站首页技术杂谈
【数据结构】树，二叉树，满二叉树，完全二叉树的定义和二叉树的基本操作
?专栏【数据结构】
?喜欢的诗句：更喜岷山千里雪 三军过后尽开颜。
?音乐分享【勋章】
大一同学小吉，欢迎并且感谢大家指出我的问题?
目录
⭐树
?️?定义
树是n（n>=0）个结点的有限集
n=0：称为空树
n>0：称为非空树
✨对于非空树，有下面两个特点
(1)有且只有一个称为根的结点
(2)除根节点之外的其余结点可以分为m(m>0)个互不相交的有限集，对于每一个有限集本身又是一棵树，并且称为根的子树
树可以有多种表示方法，如下图所示
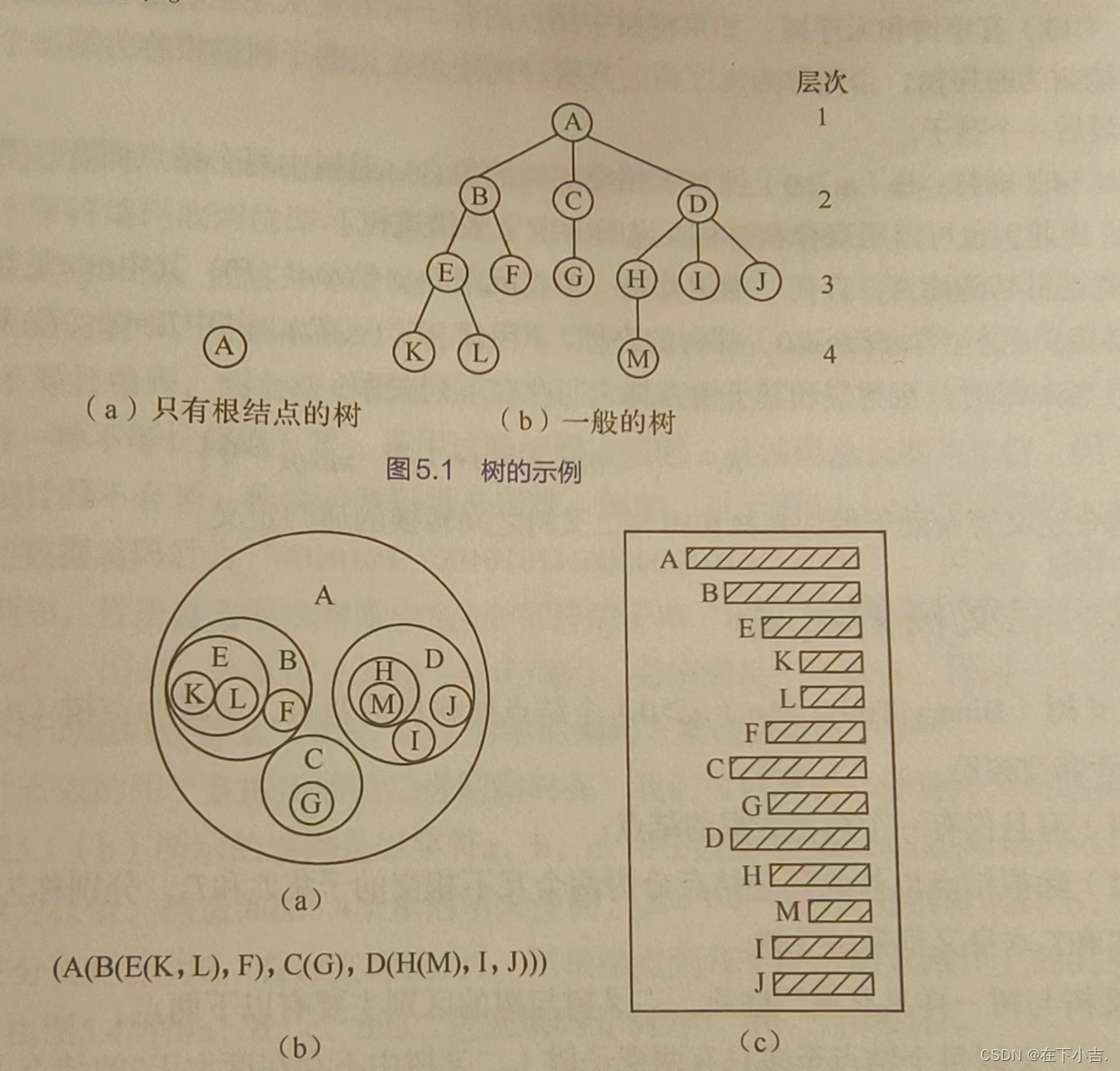
?️?注意
如下图所示
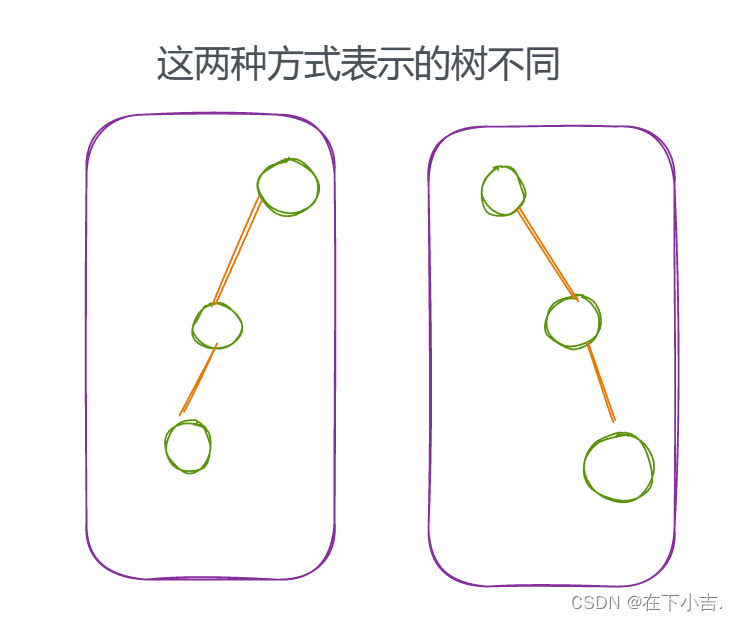
?树的基本术语
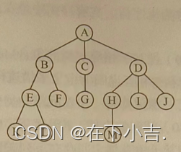
结点：树的一个独立单元（比如上图的ABCD）
结点的度：结点拥有的子树（比如上图中，A的度为3，B的度为2）
树的度：树内各结点度的最大值（比如上图的树的度为3）
叶子（终端结点）：度为0的结点
层次：结点的层次从根开始定义，根为第一层，根的孩子为第二层
树的深度（高度）：树中结点的最大层次
森林：m棵互不相交的树的集合。对于树的每个结点而言，其子树的集合就是森林
⭐二叉树
?️?定义
树是n（n>=0）个结点的有限集
n=0：称为空树
n>0：称为非空树
✨对于非空树，有下面两个特点
(1)有且只有一个称为根的结点
(2)除根节点之外的其余结点可以分为2个互不相交的子集，分别称为T的左子树T1和右子树T2，且T1T2都是二叉树
?二叉树和树的区别
?二叉树中不存在度>2的结点?
二叉树的左右子树有左右之分，不能随意颠倒
二叉树也有多种表示方法，如下图所示
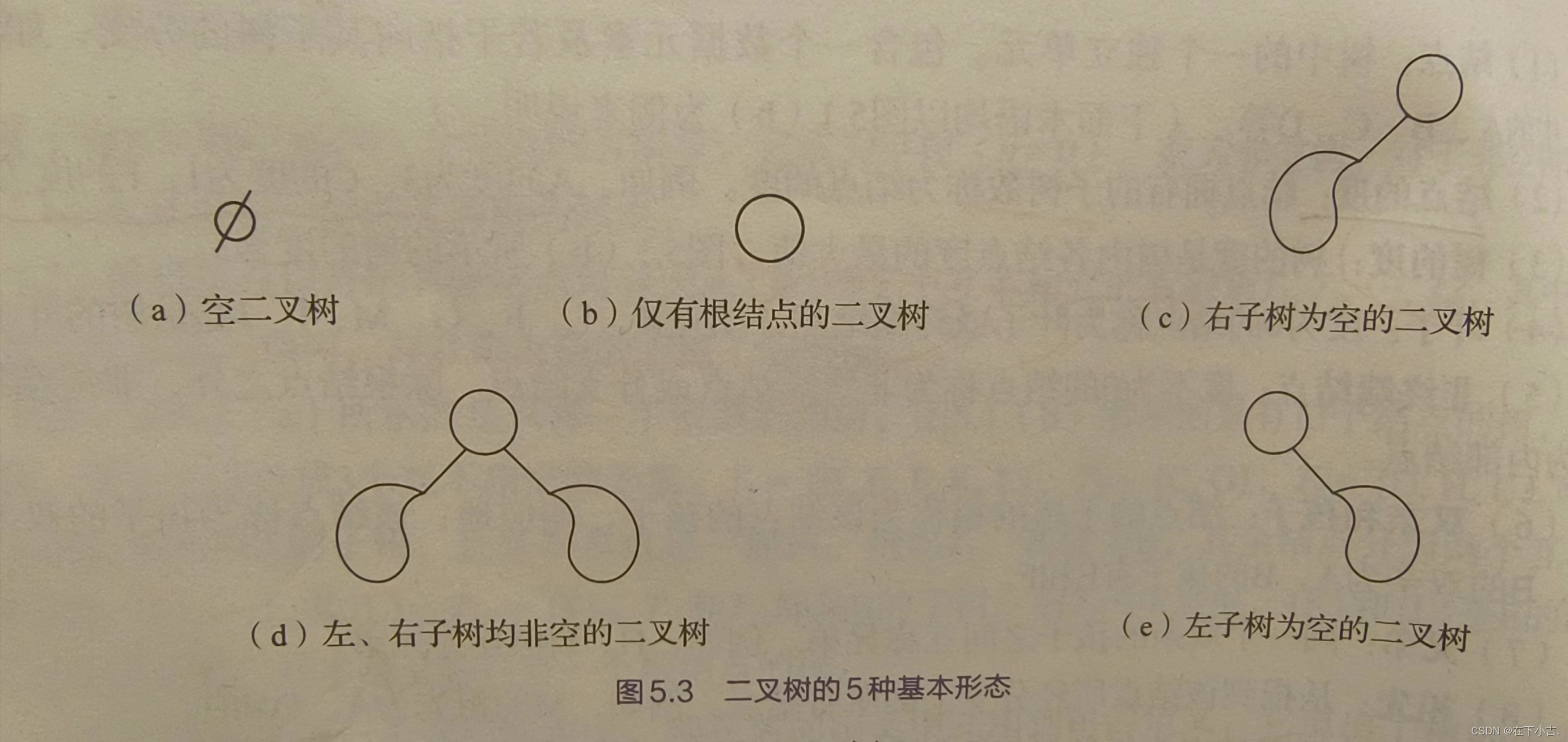
?️?二叉树的性质
?第i层上至多有2^(i-1)（i>=1）个结点
?深度为k的二叉树至多有2^k-1（k>=1）个结点
?对于任何一颗二叉树T，如果其终端结点树为n0，度为2的结点树为n2
那么n0=n2+1
⭐满二叉树
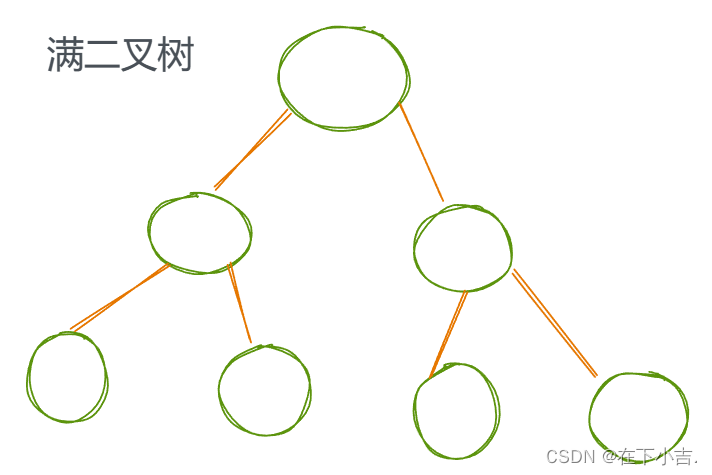
深度为k且有2^k-1个结点的二叉树，每一层的结点数都是最大结点数
⭐完全二叉树
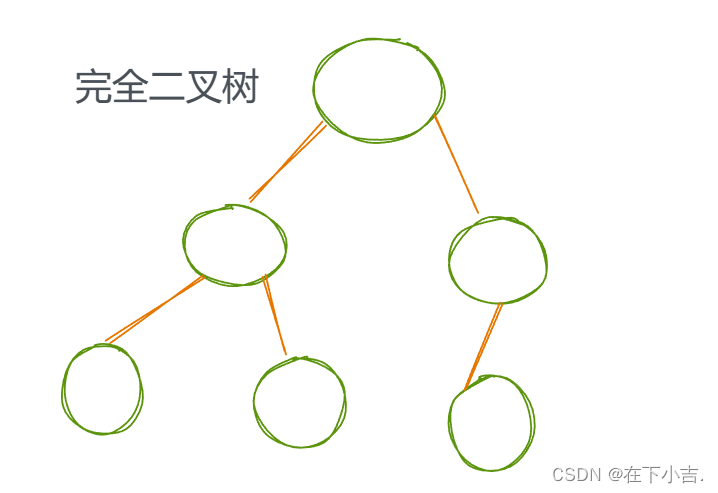
深度为k，有n个结点的二叉树，当且仅当每一个结点都与深度为k的满二叉树 中编号从1到n的结点一一对应时，为完全二叉树
文末有完整代码
?遍历二叉树
?定义
typedef struct BiNode{
char data;
struct BiNode *lchild,*rchild;
}BiNode,*BiTree;?先序遍历二叉树
操作定义如下：若二叉树为空，则操作为空；否则
(1)访问根结点；
(2)先序遍历左子树；
(3)先序遍历右子树。
void preorder_traversal(BiTree root) {
if (!root) {
return;
}
cout << root->data << " "; // 访问根节点
preorder_traversal(root->lchild); // 递归访问左子树
preorder_traversal(root->rchild); // 递归访问右子树
}
?中序遍历二叉树
操作定义如下：若二叉树为空，则操作为空；否则
(1)中序遍历左子树；
(2)访问根结点；
(3)中序遍历右子树。
void inorder_traversal(BiTree root) {
if (!root) {
return;
}
inorder_traversal(root->lchild); // 递归访问左子树
cout << root->data << " "; // 访问根节点
inorder_traversal(root->rchild); // 递归访问右子树
}?后序遍历二叉树
操作定义如下：若二叉树为空，则操作为空；否则
(1)后序遍历左子树；
(2)后序遍历右子树；
(3)访问根结点；
void postorder_traversal(BiTree root) {
if (!root) {
return;
}
postorder_traversal(root->lchild); // 递归访问左子树
postorder_traversal(root->rchild); // 递归访问右子树
cout << root->data << " "; // 访问根节点
}?构建二叉树
法一：
比如根据 ABC##DE#G##F### 这一段来构建
?算法步骤
1.读取字符序列，读入字符ch
2.如果ch是“#”，表明该二叉树为空树，即T为NULL，否则执行下面的操作
（1）申请一个内存空间T
（2）将ch赋给T->data
（3）递归创建T的左子树
（4）递归创建T的右子树
?代码
void CreateBiTree(BiTree &T){
char ch;
cin >> ch;
if(ch=='#') T=NULL;
else{
T=new BiTNode;
T->data=ch; //生成根结点
CreateBiTree(T->lchild); //递归创建左子树
CreateBiTree(T->rchild); //递归创建右子树
}
} 法二：
// 构建二叉树
BiTree root = new BiNode{'A', nullptr, nullptr};
root->lchild = new BiNode{'B', nullptr, nullptr};
root->lchild->lchild = new BiNode{'C', nullptr, nullptr};
root->lchild->rchild = new BiNode{'D', nullptr, nullptr};
root->lchild->rchild->lchild = new BiNode{'E', nullptr, nullptr};
root->lchild->rchild->lchild->rchild = new BiNode{'G', nullptr, nullptr};
root->lchild->rchild->rchild = new BiNode{'F', nullptr, nullptr};?复制二叉树
?算法步骤
1.为空树，递归结束
2.不为空树，那么执行下面的操作
（1）申请一个新结点空间，复制根节点
（2）递归复制左子树
（3）递归复制右子树
?代码
void Copy(BiTree T,BiTree &NewT)
{
if(T==NULL){
NweT=NULL;
return;
}else{
NewT=new BiTree; //复制根节点
NewT->data=T->data;
Copy(T->lchild,NewT->lchild);
Copy(T->rchild,NewT->rchild);
}
}
?计算二叉树的深度
?算法步骤
1.为空树，递归结束
2.不为空树，那么执行下面的操作
（1）递归计算左子树的深度为m
（2）递归计算右子树的深度为n
（3）如果m>n，那么二叉树深度为m+1，否则为n+1
?代码
int Depth(BiTree T)
{
int m,n;
if(T == NULL ) return 0; //如果是空树，深度为0，递归结束
else
{
m=Depth(T->lchild); //递归计算左子树的深度记为m
n=Depth(T->rchild); //递归计算右子树的深度记为n
if(m>n) return(m+1); //二叉树的深度为m 与n的较大者加1
else return (n+1);
//+1，所以可以计算出来
}
}?统计二叉树中结点的总数
?算法步骤
如果是空树，那么结点个数为0，递归结束
否则，结点个数=左子树结点个数+右子树结点个数+1
?代码
int NodeCount(BiTree T)
{
if(T==NULL) return 0; // 如果是空树，则结点个数为0，递归结束
else return NodeCount(T->lchild)+ NodeCount(T->rchild) +1;
//否则结点个数为左子树的结点个数+右子树的结点个数+1
//+1，所以可以计算出来//
} ?统计二叉树中叶子结点的个数
?算法步骤
如果是空树，那么结点个数为0，递归结束
否则，遍历到NULL，即叶子节点
?代码
int LeafCount(BiTree T){
if(T==NULL) //如果是空树返回0
return 0;
if (T->lchild == NULL && T->rchild == NULL)
return 1; //如果是叶子结点返回1
// 1，所以可以计算出来
else return LeafCount(T->lchild) + LeafCount(T->rchild);
}?完整代码
#include<iostream>
using namespace std;
typedef struct BiNode{
char data;
struct BiNode *lchild,*rchild;
}BiTNode,*BiTree;
void CreateBiTree(BiTree &T){
char ch;
cin >> ch;
if(ch=='#') T=NULL;
else{
T=new BiTNode;
T->data=ch; //生成根结点
CreateBiTree(T->lchild); //递归创建左子树
CreateBiTree(T->rchild); //递归创建右子树
}
}
void PreOrderTraverse(BiTree T)
{
if (T) {
cout<<T->data; // 访问结点
PreOrderTraverse(T->lchild); // 遍历左子树
PreOrderTraverse(T->rchild);// 遍历右子树
}
}
void InOrderTraverse(BiTree T){
if(T){
InOrderTraverse(T->lchild);
cout << T->data;
InOrderTraverse(T->rchild);
}
}
void PostOrderTraverse(BiTree T)
{
if (T) {
PostOrderTraverse(T->lchild); // 遍历左子树
PostOrderTraverse(T->rchild);// 遍历右子树
cout << T->data; // 访问结点
}
}
int NodeCount(BiTree T)
{
if(T==NULL) return 0; // 如果是空树，则结点个数为0，递归结束
else return NodeCount(T->lchild)+ NodeCount(T->rchild) +1;
//否则结点个数为左子树的结点个数+右子树的结点个数+1
//+1，所以可以计算出来//
}
//计算二叉树中叶子结点的个数
int LeafCount(BiTree T){
if(T==NULL) //如果是空树返回0
return 0;
if (T->lchild == NULL && T->rchild == NULL)
return 1; //如果是叶子结点返回1
// 1，所以可以计算出来
else return LeafCount(T->lchild) + LeafCount(T->rchild);
}
//计算二叉树的深度
int Depth(BiTree T)
{
int m,n;
if(T == NULL ) return 0; //如果是空树，深度为0，递归结束
else
{
m=Depth(T->lchild); //递归计算左子树的深度记为m
n=Depth(T->rchild); //递归计算右子树的深度记为n
if(m>n) return(m+1); //二叉树的深度为m 与n的较大者加1
else return (n+1);
//+1，所以可以计算出来
}
}
int main(){
BiTree tree;
int nodecount=0,leafcount=0,depth=0;
cout<<"请输入建立二叉链表的序列：
";
CreateBiTree(tree);
cout<<endl;
cout<<"先序遍历的结果为：
";
PreOrderTraverse(tree);
cout<<endl;
cout<<"中序遍历的结果为：
";
InOrderTraverse(tree);
cout<<endl;
cout<<"后序遍历的结果为：
";
PostOrderTraverse(tree);
cout<<endl;
cout<<"该二叉树中结点总数为：";
cout<<NodeCount(tree)<<endl;
cout<<"该二叉树中叶子结点总数为：";
cout<<LeafCount(tree)<<endl;
cout<<"该二叉树的深度为：";
cout<<Depth(tree)<<endl;
return 0;
}
?如果大家有不明白的地方，或者文章有问题，欢迎大家在评论区讨论，指正?
站长推荐
- SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权 - stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程） - U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 - 【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》 - 【云原生进阶之容器】第六章容器网络6.6.1--Cilium网络方案概述
【云原生进阶之容器】第六章容器网络6.6.1--Cilium网络方案概述