题目一（贪心）

❓674. 最长连续递增序列

难度：简单

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。

示例 1：

输入：nums = [1,3,5,4,7]
输出：3
解释：最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。

示例 2：

输入：nums = [2,2,2,2,2]
输出：1
解释：最长连续递增序列是 [2], 长度为1。

提示：

• $1<=nums.length<=10^4$
• $-10^9<=nums[i]<=10^9$

?思路：贪心

这道题目可以用贪心来做：

• 遇到 nums[i] > nums[i - 1] 的情况，count就++，
• 否则count为1，使用ans保存count的最大值。

?代码：(Java、C++)

Java

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int ans = 1, count = 1;;
        for(int i = 1; i < nums.length; i++){
            if(nums[i] > nums[i - 1]) count++;
            else{
                ans = Math.max(ans, count);
                count = 1;
            }
        }
        ans = Math.max(ans, count);
        return ans;
    }
}

C++

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int ans = 1, count = 1;;
        for(int i = 1; i < nums.size(); i++){
            if(nums[i] > nums[i - 1]) count++;
            else{
                ans = max(ans, count);
                count = 1;
            }
        }
        ans = max(ans, count);
        return ans;
    }
};

? 运行结果：

? 复杂度分析：

• 时间复杂度：$O(n)$，其中 n 为数组nums的长度，要遍历数组一次。
• 空间复杂度：$O(1)$，额外使用的空间为常数。

题目来源：力扣。

题目二（背包问题）

❓718. 最长重复子数组

难度：中等

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

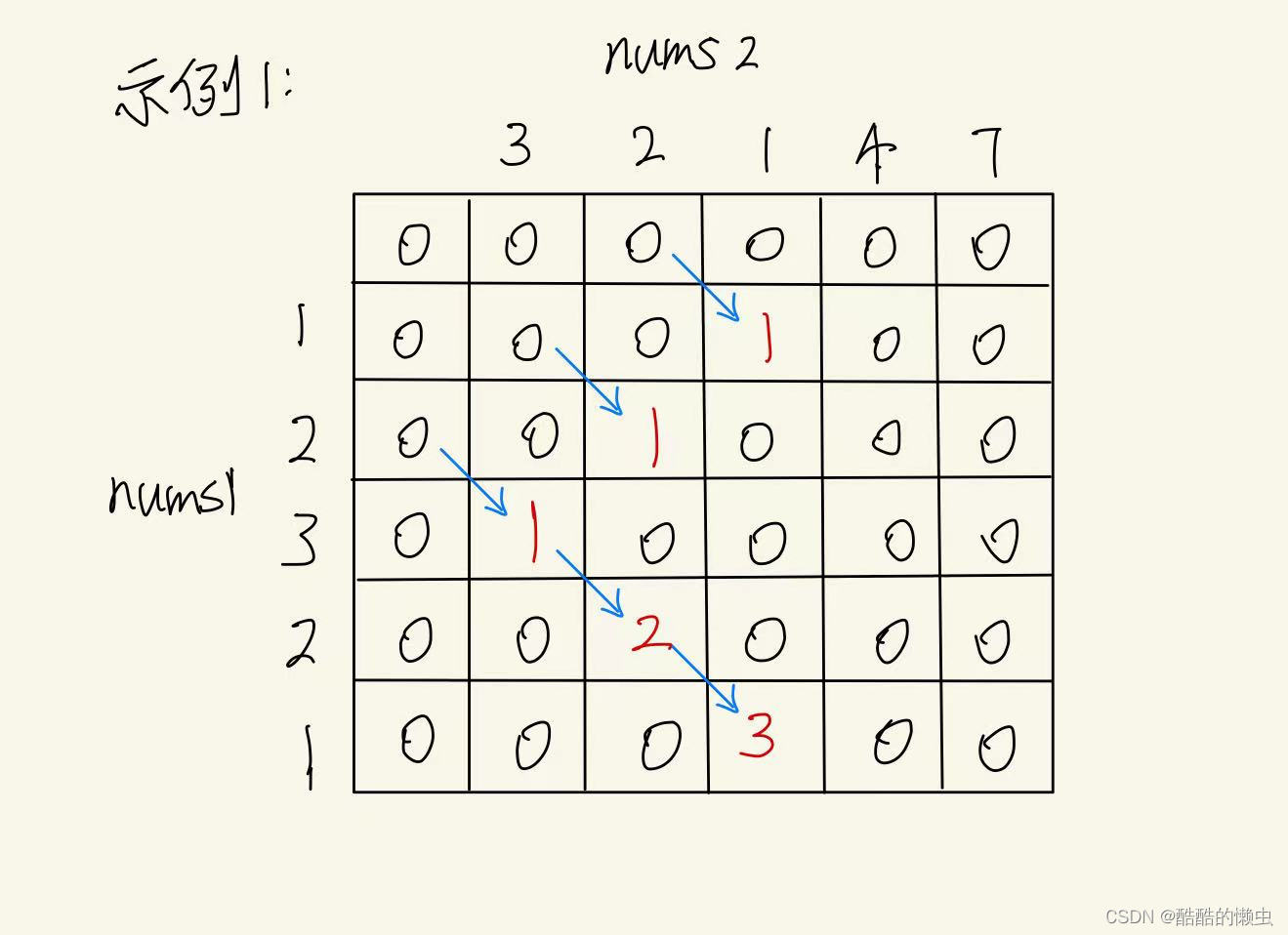
示例 1：

输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3,2,1] 。

示例 2：

输入：nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出：5

提示：

• 1 <= nums1.length, nums2.length <= 1000
• 0 <= nums1[i], nums2[i] <= 100

?思路：动态规划

背包问题必知内容：一篇文章吃透背包问题！！！

类似 0-1背包，我们可以设置一个二维dp数组，dp[i][j] 表示nums1的前i个数字 和 nums2的前j个数字 的最长重复子数组长度：

• 如果nums1[i] == nums2[j]则此时的最长长度等于左上角的长度加1 ,即状态转移公式为：
  $$dp[i][j]=dp[i-1][j-1]+1$$
• 如果不相等，dp[i][j] = 0；

⭐️ 空间优化：

• 由上面的 状态转移公式 发现，dp[i][j] 只与 dp[i-1][j-1]有关，所以可以只使用一维 dp 数组即可，即状态转移公式 可变为：
  $$dp[j]=1+dp[j-1]$$
• 又因为 dp[j] 使用的是变化前的dp[j-1],所以在程序实现时需要按 倒序 来循环求解。

?代码：(Java、C++)

Java

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int[] dp = new int[nums2.length + 1];//dp[i]数组存储
        int ans = 0;
        for(int i = 0; i < nums1.length; i++){
            for(int j = nums2.length - 1; j >= 0; j--){
                if(nums1[i] == nums2[j]){
                    dp[j + 1] = 1 + dp[j];
                    ans = Math.max(ans, dp[j + 1]);
                } 
                else dp[j + 1] = 0;
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<int> dp(nums2.size() + 1);//dp[i]数组存储
        int ans = 0;
        for(int i = 0; i < nums1.size(); i++){
            for(int j = nums2.size() - 1; j >= 0; j--){
                if(nums1[i] == nums2[j]){
                    dp[j + 1] = 1 + dp[j];
                    ans = max(ans, dp[j + 1]);
                } 
                else dp[j + 1] = 0;
            }
        }
        return ans;
    }
};

? 运行结果：

? 复杂度分析：

• 时间复杂度：$O(n\ast m)$，其中 n 为数组nums1的长度，m 为数组nums2的长度。
• 空间复杂度：$O(m)$。

题目来源：力扣。

放弃一件事很容易，每天能坚持一件事一定很酷，一起每日一题吧！
关注我LeetCode主页 / CSDN —— 力扣专栏，每日更新！

注： 如有不足，欢迎指正！