您现在的位置是:首页 >技术交流 >算法设计与分析:贪心法网站首页技术交流
算法设计与分析:贪心法
目录
第一关:贪心法
任务描述:
本关任务:完成 乘船问题 ;
相关知识:
为了完成本关任务,你需要掌握:贪心法。
贪心法,又称贪婪算法是一种解决问题的策略。是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法。如果策略正确,那么贪心法往往是易于描述、易于实现的。
贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择,不能回退。动态规划则会保存以前的运算结果,并根据以前的结果对当前进行选择,有回退功能。
贪心法的优缺点:
贪心法可以解决一些最优化问题,如:求图中的最小生成树、求哈夫曼编码……对于其他问题,贪心法一般不能得到我们所要求的答案。一旦一个问题可以通过贪心法来解决,那么贪心法一般是解决这个问题的最好办法。由于贪心法的高效性以及其所求得的答案比较接近最优结果,贪心法也可以用作辅助算法或者直接解决一些要求结果不特别精确的问题。
下面通过一个简单的实例题目对贪心进行详解:
例题:
乘船问题: 给出 n 个人,第 i 个人重量为 wi 。每艘船的最大载重量均为 C,且最多只能乘两个人。用最少的船装载所有人。有解输出船的个数,无解输出 “no”。
解题分析:
考虑最轻的人i,如果每个人都无法和他一起坐船,则唯一的方法就是每个人一艘船。否则,他应该选择能和他一起坐船的人中最重的一个j。这样的方法是贪心的,因此它只是让眼前的浪费最少。
程序实现:
将人的重量按照从小到大排序。比j更重的人只能每人坐一艘船。这样,只需要两个下表i和j分别表示当前考虑的最轻的人和最重的人,每次先将j往左移动,直到i和j可以共坐一艘船,然后将i+1,j-1,并重复上述操作。
关键代码:
int p=0,q=n-1,s=0; // p代表左索引,q代表右索引
if(a[q]>c) cout<<"no"<<endl; // 如果最大的体重(最右边索引的人)大于船的最大载重,那么直接输出 no
else{
for(int i=0;i<n;i++){ // 遍历所有人
if(p>q) break;
if(a[p]+a[q]>c) q--; // 如果最小体重的人和当前最大的人不能同船,那么当前体重最大的人就要一个人一个船。
else p++,q--; // 当前体重最小的人和当前体重最大的人同船
s++;
}
cout<<s<<endl;
}时间复杂度:不难看出,程序的时间复杂度仅为O(n)。是最优算法。
编程要求:
根据提示,在右侧编辑器补充代码,完成乘船问题。
测试说明:
平台会对你编写的代码进行测试:
测试输入:
6 855 84 85 80 84 83
预期输出: 5
测试输入:
10 855 84 85 80 84 83 55 77 6 11
预期输出: 7
#include<iostream>
using namespace std;
const int maxn=10000;
void fast_sort(int *a,int begin,int end){
int l,r,m;
l=begin,r=end,m=(begin+end)>>1;
while(l<=r){
while(a[l]<a[m]) l++;
while(a[r]>a[m]) r--;
if(l<=r){
int t=a[l];
a[l]=a[r];
a[r]=t;
l++;
r--;
}
}
if(l<end) fast_sort(a,l,end);
if(begin<r) fast_sort(a,begin,r);
}
int main(){
int n,c;
int a[maxn];
/********** Begin **********/
cin>>n>>c;
for(int i=0;i<n;i++){
cin>>a[i];
}
fast_sort(a,0,n-1);
int p=0,q=n-1,s=0; // p代表左索引,q代表右索引
if(a[q]>c) cout<<"no"<<endl; // 如果最大的体重(最右边索引的人)大于船的最大载重,那么直接输出 no
else{
for(int i=0;i<n;i++){ // 遍历所有人
if(p>q) break;
if(a[p]+a[q]>c) q--; // 如果最小体重的人和当前最大的人不能同船,那么当前体重最大的人就要一个人一个船。
else p++,q--; // 当前体重最小的人和当前体重最大的人同船
s++;
}
cout<<s<<endl;
}
/********** End **********/
return 0;
}
第二关:最小生成树
任务描述:
本关任务:理解并实现无向图的最小生成树
相关知识:
为了完成本关任务,你需要掌握:贪心算法。
最小生成树概念:
最小生成树是一副连通加权无向图中一棵权值最小的生成树。在一给定的无向图 G = (V, E) 中,(u, v) 代表连接顶点 u 与顶点 v 的边(即 (u,v)∈E),而w(u,v)代表此边的权重,若存在 T 为 E 的子集(即T⊆E)且 (V, T) 为树,使得的w(T)最小,则此T为G的最小生成树。最小生成树其实是最小权重生成树的简称。 W(T)=∑(u,v)∈Tw(u,v)
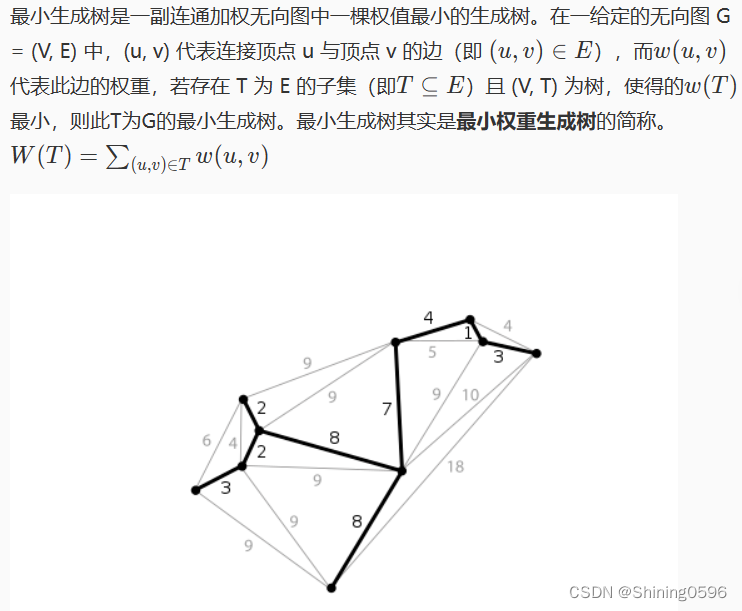
一个连通图可能有多个生成树。当图中的边具有权值时,总会有一个生成树的边的权值之和小于或者等于其它生成树的边的权值之和。
Kruskal算法:
不停地循环,每一次都寻找两个顶点,这两个顶点不在同一个真子集里,且边上的权值最小。
把找到的这两个顶点联合起来。
初始时,每个顶点各自属于自己的子集合,共n个子集合。
每一步操作,都会将两个子集合融合成一个,进而减少一个子集合。
结束时,所有的顶点都在同一个子集合里,这个子集合就是最小生成树。
贪心策略:
贪心策略就是,每次都选择权重最小的但未形成环路的边加入到生成树中。
算法图解:
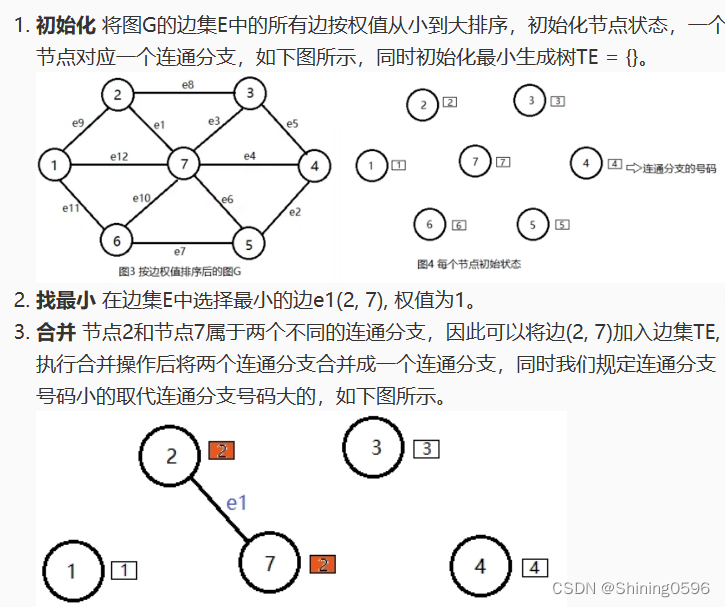
图5 最小生成树的求解过程

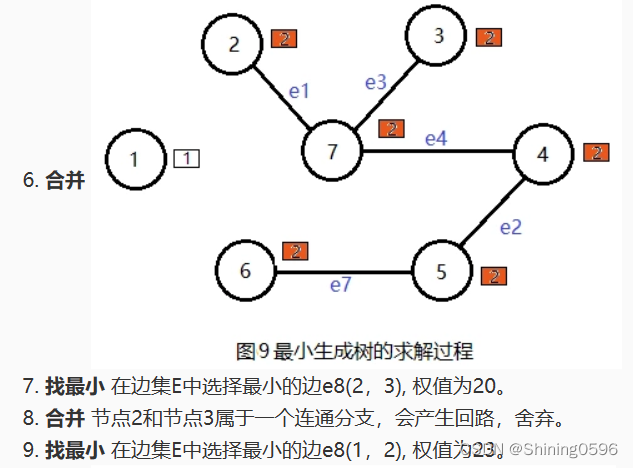
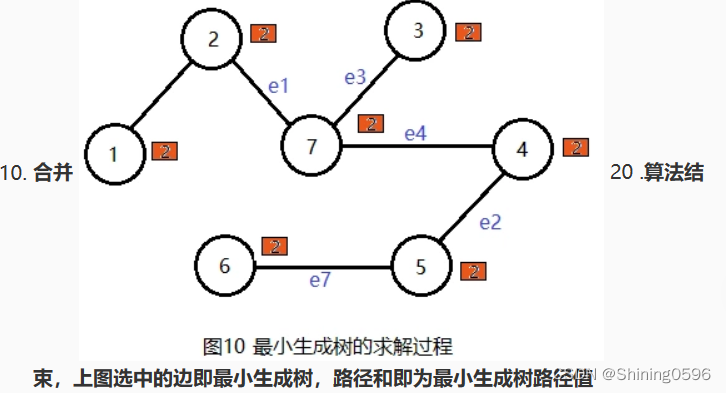

思路再分析:
在上面的过程中,最关键的地方在于”连通分量的查询与合并“:需要知道任意两个点是否在同一个连通分量重,还需要合并两个连通分量。 最容易想到的方法是”暴力 “解决。在输入时,创建一个数组,记录下一个节点的值。在创建时,每个节点的下一个值为自己本身值。连通时,判断两个节点值是否相等。相等,就会形成回路,不相等,就将第一个节点的下一个节点值设置为第二个节点值。可是遗憾的时,这个方法不仅复杂,而且效率不高。
并查集。有一种简洁高效的方法可以用来处理这个问题:使用并查集+路径压缩算法。由于本章只阐述贪心算法,对这部分内容不进行详解,有兴趣的可以自行查找资料。
编程要求:
根据提示,在右侧编辑器 Begin-End 区间补充代码,完成最小生成树问题。
测试说明:
输入数据: 第一行。输出两个数。n和m。 后面有n行,对应着n条路径,每行三个值。前两个代表两个点,第三个表示两个点的距离。 m代表有m个点。求m个点的最小生成树的路径值。 输出数据: 一个数,为最少权值。
平台会对你编写的代码进行测试:
测试输入:
10 61 3 11 2 61 4 52 3 52 5 33 5 65 6 63 4 53 6 44 6 2
预期输出: 15
#include<bits/stdc++.h>
using namespace std;
int n,m;//n为节点总数,m为边数
int ans=0;//ans记录最小权值,
int k=0;//k记录已连接的边数
int fat[200010];//记录根节点
struct node//结构体储存边
{
int from,to,dis;
}edge[200010];
bool cmp(node a,node b)//sort排序 从小到大排列
{
return a.dis<b.dis;
}
int father(int x)//找根节点,并查集的查
{
if(fat[x]!=x)
return father(fat[x]);
else return x;
}
void unionn(int x,int y)//加入集合,并查集的并
{
fat[father(y)]=father(x);
}
int main()
{
cin>>m>>n;
for(int i=1;i<=m;i++)
{
cin>>edge[i].from>>edge[i].to>>edge[i].dis;
}
for(int i=1;i<=n;i++) //初始化 没加边之前 每个节点的根节点都是自己
{
fat[i]=i;
}
sort(edge+1,edge+1+m,cmp); //排序后,从最小的边开始,满足更新节点就加入集合
for(int i=1;i<=m;i++)
{
if(k==n-1) break;//连接n个点需要n-1条边
if(father(edge[i].from)!=father(edge[i].to))//节点是否更新
{
unionn(edge[i].from,edge[i].to);//加入集合
ans+=edge[i].dis;//加上权值
k++;//边数加1
}
}
cout<<ans;
return 0;
}
第3关:Huffman 编码
任务描述:
本关任务:理解并实现Huffman编码树 ;
相关知识:
为了完成本关任务,你需要掌握:
- c++基础;
- 二叉树;
最小生成树概念:
哈夫曼(Huffman)编码算法是基于二叉树构建编码压缩结构的,它是数据压缩中经典的一种算法。算法根据文本字符出现的频率,重新对字符进行编码。因为为了缩短编码的长度,我们自然希望频率越高的词,编码越短,这样最终才能最大化压缩存储文本数据的空间。
假设现在我们要对下面这句歌词“we will we will r u”进行压缩。我们可以想象,如果是使用ASCII码对这句话编码结果则为:119 101 32 119 105 108 108 32 119 101 32 119 105 108 108 32 114 32 117(十进制表示)。我们可以看出需要19个字节,也就是至少需要152位的内存空间去存储这些数据。
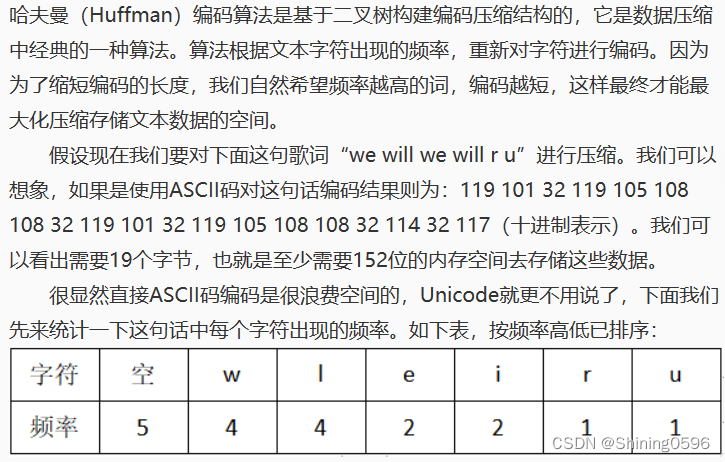
题目:
最优编码问题。给出n个字符的频率ci,给每个字符赋予一个01编码串,使得任意一个字符穿的编码不是另一个字符编码的前缀,而且编码后总长度(每个字符的频率与编码长度乘积的综和)尽量小。
如何构造一棵最优的编程树:
Huffman算法:把每个字符看作一个单结点子树放在一个树集合中,每棵子树的权值等于相应字符的频率。每次取权值最小的两棵子树合并成一棵新树,并重新放到集合中。新树的权值等于两颗子树权值之和。
下面分两步证明算法的正确性。 结论1:设x和y是频率最小的两个字符,则存在前缀码使得x和y具有相同码长,且仅有最后一个编码不同。换句话说。第一步贪心选择法保留最优解。 证明 :假设深度最大的节点为a,则a一定有一个兄弟b。设f(x)≤f(y),f(a)≤f(b),则f(x)≤f(a),f(y)≤f(b)。如果x不是a,则交换x和a;如果y不是b,则交换y和b。这样得到的新编码树不会比原来的差。
结论2: 设T是加权字符集C的最优编码树,x和y是树T中两个叶子,且互为兄弟结点,z是它们的父节点。若把z看成具有频率f(z)=f(x)+f(y)的字符,则树T˙=C−x,y∪z的一棵最优编码树。换句话说,原问题的最优解包含子问题的最优解。 证明: 设T˙的编码长度为L,其次字符{x,y}的深度为h,则把字符{x,y}拆成两个后,长度变为L−(f(x)+f(y))。因此T˙必须是C˙的最优编码树 ,T才是C的最优编码树。

结论:
结论1: 通常称为贪心选择性质; 结论2: 通常称为最优子结构性质。根据这两个结论,Huffman算法正确。在程序实现上,可以先按照频率把所有字符排序成表P,然后创建一个新结点队列Q,在每次合并两个结点后把新结点放到队列Q中。由于后合并的频率和一定比先合并的频率和大,因此Q内的元素是有序的。类似有序表的合并过程,每次只需要检查P和Q的首元素即可找到频率最小的元素,时间复杂度为O(n)。算上排序,总时间复杂度为O(nlogn)。

编程要求:
根据提示,在右侧编辑器 Begin-End 区间补充代码,完成Huffman编码树问题。
测试说明:
平台会对你编写的代码进行测试:
输入数据: 第一行,一个输入(n),n表示有n行。后面两行,第一个值是字符,第二个值是频率。输出一行,为多少位内存空间。 $内存空间=一个字符串的位编码长度*频率$ 输出数据: 最短编码长度
测试输入:
6a 45b 13c 12d 16e 9f 5
预期输出: 224
#include<bits/stdc++.h>
using namespace std;
typedef struct//哈夫曼树的存储表示
{
char s;
int weight; //权值
int parent, lChild, rChild; //双亲及左右孩子的下标
}HTNode, *HuffmanTree;
void Select(HuffmanTree hT, int n, int &s1, int &s2)//选择两个最小节点
{
s1 = s2 = 0;
int i;
for(i = 1; i < n; ++ i)//选择两个未有双亲的节点
{
if(hT[i].parent == 0)
{
if(0 == s1)
{
s1 = i;
}
else
{
s2 = i;
break;//后面一个for循环的标记
}
}
}
if(hT[s1].weight > hT[s2].weight)//确保s1>s2
{
int t = s1;
s1 = s2;
s2 = t;
}
for(i+=1;i<n;++i)//选择s2即break 故从i+1开始选择两个最小节点
{
if(hT[i].parent==0)
{
if(hT[i].weight < hT[s1].weight)
{
s2 = s1;
s1 = i;
}
else if(hT[i].weight < hT[s2].weight)
{
s2 = i;
}
}
}
//cout<<s1<<" "<<s2<<"**"<<endl;
}
void CreateHufmanTree(HuffmanTree &hT)//构造哈夫曼树
{
int n,m;
cin>>n;
m = 2*n - 1;
hT = new HTNode[m + 1];
hT[0].weight=m; // 0号节点用来记录节点数量
for(int i = 1; i <= m; ++ i)
{
hT[i].parent = hT[i].lChild = hT[i].rChild = 0;//初始化
}
for(int i = 1; i <= n; ++ i)
{
cin >>hT[i].s>>hT[i].weight; // 输入权值
}
for(int i = n + 1; i <= m; ++ i)//建立过程
{
int s1, s2;
Select(hT, i, s1, s2);
hT[s1].parent = hT[s2].parent = i;
hT[i].lChild = s1; hT[i].rChild = s2; //作为新节点的孩子
hT[i].weight = hT[s1].weight + hT[s2].weight; //新节点为左右孩子节点权值之和
}
}
int HuffmanTreeWPL_(HuffmanTree hT, int i, int deepth)//递归计算WPL
{
if(hT[i].lChild == 0 && hT[i].rChild == 0)
{
return hT[i].weight * deepth;
}
else
{
return HuffmanTreeWPL_(hT, hT[i].lChild, deepth + 1) + HuffmanTreeWPL_(hT, hT[i].rChild, deepth + 1);
}
}
int HuffmanTreeWPL(HuffmanTree hT)//计算WPL
{
return HuffmanTreeWPL_(hT, hT[0].weight, 0);
}
void DestoryHuffmanTree(HuffmanTree &hT)//销毁哈夫曼树
{
delete[] hT;
hT = NULL;
}
int main()
{
HuffmanTree hT;
CreateHufmanTree(hT);
cout << HuffmanTreeWPL(hT) << endl;
DestoryHuffmanTree(hT);
return 0;
}
第4关:单源点最短路径
任务描述:
本关任务:理解并实现单源点最短路径
相关知识:
为了完成本关任务,你需要掌握:
- 贪心法;
- Dijkstra算法;
单源点最短路径:
给定一个带权有向图G=(V,E),其中每条边的权是一个实数。另外,还给定V中的一个顶点,称为源。要计算从源到其他所有各顶点的最短路径长度。这里的长度就是指路上各边权之和。这个问题通常称为单源最短路径问题。
Dijkstra算法:
解决单源最短路径问题的方法之一就是Dijkstra算法。Dijkstra算法会生成一颗最短路径树,树的根为起始顶点s, 树的分支为从顶点s到图G中所有其他顶点的最短路径。此算法要求图中的所有权值均为非负数。与Prim算法类似,Dijkstra算法也采用贪心算法,它总是将当前看起来最近的最短的边加入最短路径中。
从根本上来说,Dijkstra算法通过选择一个顶点,并不断探测与之相关的边,类似广度优先搜索,找出当前距离最近的点。
图片说明:
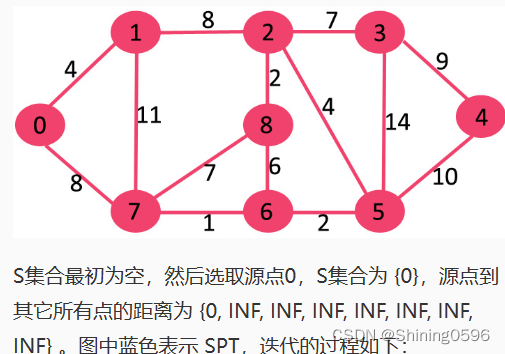
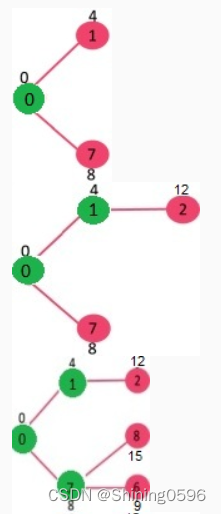
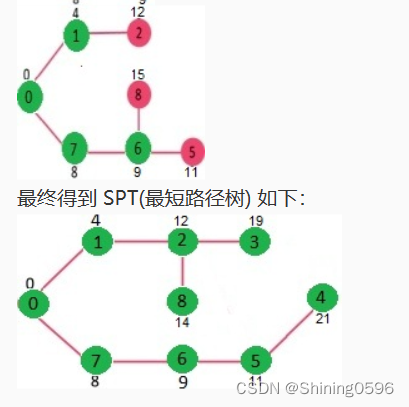
具体实现图:
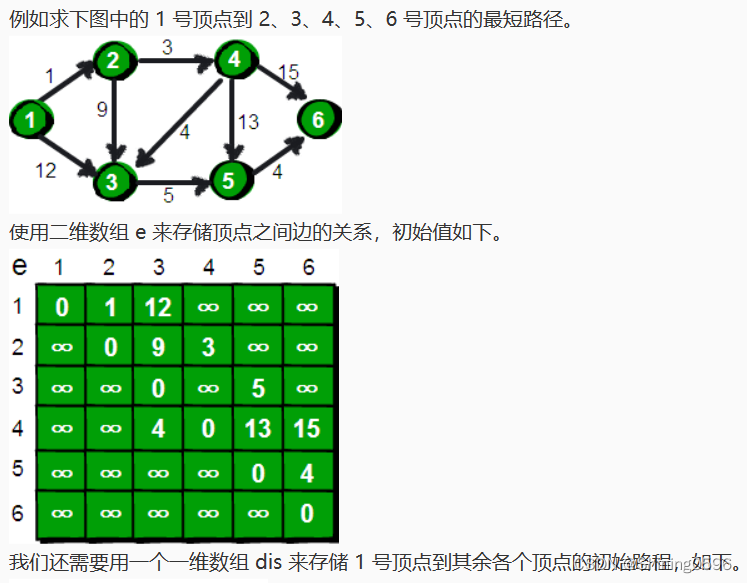

既然是求 1 号顶点到其余各个顶点的最短路程,那就先找一个离 1 号顶点最近的顶点。通过数组 dis 可知当前离 1 号顶点最近是 2 号顶点。当选择了 2 号顶点后,dis[2]的值就已经从“估计值”变为了“确定值”,即 1 号顶点到 2 号顶点的最短路程就是当前 dis[2]值。为什么呢?你想啊,目前离 1 号顶点最近的是 2 号顶点,并且这个图所有的边都是正数,那么肯定不可能通过第三个顶点中转,使得 1 号顶点到 2 号顶点的路程进一步缩短了。因为 1 号顶点到其它顶点的路程肯定没有 1 号到 2 号顶点短,对吧 O(∩_∩)O~
既然选了 2 号顶点,接下来再来看 2 号顶点有哪些出边呢。有 2->3 和 2->4 这两条边。先讨论通过 2->3 这条边能否让 1 号顶点到 3 号顶点的路程变短。也就是说现在来比较 dis[3]和 dis[2]+e[2][3]的大小。其中 dis[3]表示 1 号顶点到 3 号顶点的路程。dis[2]+e[2][3]中 dis[2]表示 1 号顶点到 2 号顶点的路程,e[2][3]表示 2->3 这条边。所以 dis[2]+e[2][3]就表示从 1 号顶点先到 2 号顶点,再通过 2->3 这条边,到达 3 号顶点的路程。
我们发现 dis[3]=12,dis[2]+e[2][3]=1+9=10,dis[3]>dis[2]+e[2][3],因此 dis[3]要更新为 10。这个过程有个专业术语叫做“松弛”。即 1 号顶点到 3 号顶点的路程即 dis[3],通过 2->3 这条边松弛成功。这便是 Dijkstra 算法的主要思想:通过“边”来松弛 1 号顶点到其余各个顶点的路程。
同理通过 2->4(e[2][4]),可以将 dis[4]的值从 ∞ 松弛为 4(dis[4]初始为 ∞,dis[2]+e[2][4]=1+3=4,dis[4]>dis[2]+e[2][4],因此 dis[4]要更新为 4)。
刚才我们对 2 号顶点所有的出边进行了松弛。松弛完毕之后 dis 数组为:


OK,现在来总结一下刚才的算法。算法的基本思想是:每次找到离源点(上面例子的源点就是 1 号顶点)最近的一个顶点,然后以该顶点为中心进行扩展,最终得到源点到其余所有点的最短路径。基本步骤如下:
- 将所有的顶点分为两部分:已知最短路程的顶点集合 P 和未知最短路径的顶点集合 Q。最开始,已知最短路径的顶点集合 P 中只有源点一个顶点。我们这里用一个 book[ i ]数组来记录哪些点在集合 P 中。例如对于某个顶点 i,如果 book[ i ]为 1 则表示这个顶点在集合 P 中,如果 book[ i ]为 0 则表示这个顶点在集合 Q 中。
- 设置源点 s 到自己的最短路径为 0 即 dis=0。若存在源点有能直接到达的顶点 i,则把 dis[ i ]设为 e[s][ i ]。同时把所有其它(源点不能直接到达的)顶点的最短路径为设为 ∞。
- 在集合 Q 的所有顶点中选择一个离源点 s 最近的顶点 u(即 dis[u]最小)加入到集合 P。并考察所有以点 u 为起点的边,对每一条边进行松弛操作。例如存在一条从 u 到 v 的边,那么可以通过将边 u->v 添加到尾部来拓展一条从 s 到 v 的路径,这条路径的长度是 dis[u]+e[u][v]。如果这个值比目前已知的 dis[v]的值要小,我们可以用新值来替代当前 dis[v]中的值。
- 重复第 3 步,如果集合 Q 为空,算法结束。最终 dis 数组中的值就是源点到所有顶点的最短路径。
编程要求:
根据提示,在右侧编辑器补充代码,完成单源点最短路径问题。
测试说明:
平台会对你编写的代码进行测试:
输入数据: 第一行,一个输入(n),n表示有n条边。后面n行,每行三个值,前两个是顶得,第三个是距离。输出n行,顶得到所有结点的距离。 输出数据: 起点到任意点的最短路径的距离。
测试输入:
7v1 v2 10v2 v3 50v3 v4 20v3 v5 10v4 v5 60v1 v5 100v1 v4 30
预期输出:
v1 0v2 10v4 30v3 50v5 60
#include<iostream>
using namespace std;
/********** Begin **********/
#define N 100
#define Min(a,b) a>b?b:a
#define INF 1000
int dis[N], bj[N];
int mp[N][N];
int n;
void djsk(int v, char** names)
{
int i, j, k, min;
for (i = 0; i < n; i++)
dis[i] = mp[v][i];//初始化dis数组,代表从起始点到i点的最短距离
dis[v] = 0;// v 代表起始节点 自己到自己为0
bj[v] = 1;// 标记 已找到短路
cout << names[0] << " " << dis[0] << endl;
for (i = 0; i < n; i++)// i 代表已经找到的最短路条数
{
min = INF; k = 0;
for (j = 0; j < n; j++)//从未找到最短路径元素中找一个路径最短的
if (!bj[j] && dis[j] < min) { min = dis[j], k = j; }
if (k != 0)
cout << names[k] << " " << dis[k] << endl;
bj[k] = 1;// 标记 已找到短路
for (j = 0; j < n; j++)//用但前最短路节点更新未找到最短路的节点
if (dis[j] > (dis[k] + mp[k][j]))dis[j] = dis[k] + mp[k][j];
}
}
/********** End **********/
int main(){
/********** Begin **********/
cin >> n;
char** names = new char* [5];
char from[3], to[3];
int len;
for (int i = 0; i < 5; i++) {
names[i] = new char[5];
names[i][0] = 'v';
names[i][1] = (i + 1) + '0';
names[i][2] = 0;
dis[i] = INF;
for (int j = 0; j < 5; j++) {
mp[i][j] = INF;
}
}
fflush(stdin);
for (int i = 0; i < n; i++) {
cin >> from;
cin >> to;
cin >> len;
mp[from[1] - '0' - 1][to[1] - '0' - 1] = len;
mp[to[1] - '0' - 1][from[1] - '0' - 1] = len;
}
n = 5;
djsk(0, names);
for (int i = 0; i < 5; i++) {
delete[] names[i];
}
delete[] names;
/********** End **********/
return 0;
}






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结