一、冒泡排序

定义：相邻的数据两两比较，小的 放前面，大的放后面

过程：

1. 相邻的元素两两比较，小的放左边，大的放右边。
2. 第一轮比较完毕之后，最大值就已经确定，第二轮可以少循环一次，后面以此类推。
3. 如果数组中有n个数据，总共我们只要执行n-1轮的代码就可以。

    private static void bubbleSort(int[] arr) {
    	//确定排序多少次，总长度-1
        for (int i = 0; i < arr.length - 1; i++) {
        	// 每一轮排序，从0开始比较，两两比较；每过一轮，去除末尾数，不进行比较
        	// -1是为了防止索引越界
            for (int j = 0; j < arr.length - 1 - i; j++) {
                if (arr[j] > arr[j+1]) {
                	// 交换位置
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
        }
        for (int k = 0; k < arr.length; k++) {
            System.err.print(arr[k] + " ");
        }
    }

二、选择排序

定义： 从0索引开始，拿着每一个索引上的元素跟后面的元素依次比较，小的放前面，大的放后面，以此类推。
过程：

1. 从0索引开始，跟后面的元素一一比较
2. 小的放前面，大的放后面。
3. 第一轮循环结束后，最小的数据已经确定
4. 第二轮循环从1索引开始以此类推。
5. 第三轮循环从2索引开始以此类推。

    private static void selectSort(int[] arr) {
    	// 外循环，从0开始，跟后面的每个数值比较
        for (int i = 0; i < arr.length-1; i++) {
        	// 内循环，从i后面遍历数据
            for (int j = i+1; j < arr.length; j++) {
                if (arr[i] > arr[j]) {
                    int temp = arr[j];
                    arr[j] = arr[i];
                    arr[i] = temp;
                }
            }
        }

        for (int k = 0; k < arr.length; k++) {
            System.err.print(arr[k] + " ");
        }
    }

三、插入排序

定义：将0索引的元素到N索引的元素看做是有序的，把N+1索引的元素到最后一个当成是无序的。遍历无序的数据，将遍历到的元素插入有序序列中适当的位置，如遇到相同数据，插在后面。

	 private static void insertSort(int[] arr) {
        // 把数组分成两部分，一部分有序，一部分无序
        int index = -1;
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] > arr[i+1]) {
                // 获取到无序索引位置
                index = i + 1;
                break;
            }
        }
        System.err.println(index);

        // 外循环， 循环无序部分 7,1,12,23,9
        for (int j = index; j < arr.length; j++) {
            int k = j;
            // 内循环， 循环有序部分 3,5,8
	
			// 方法一
            for (int m = k-1; m >= 0; m--) {
                // 循环一次，索引向前移动一位
                if (arr[m] > arr[k]) {
                    int temp = arr[k];
                    arr[k] = arr[m];
                    arr[m] = temp;
                    k--;
                } else {
                	// 当前面的小于后面的，本轮排序完成，直接跳出循环
                    break;
                }
            }
            
			// 方法二
			while(k >= 1 && arr[k]< arr[k - 1])(//交换位置
				int temp = arr[k];
				arr[k] = arr[k - 1];
				arr[k - 1] = temp;
				k--;
			}

        }
        for (int s = 0; s < arr.length; s++) {
            System.err.print(arr[s] + " ");
        }
    }

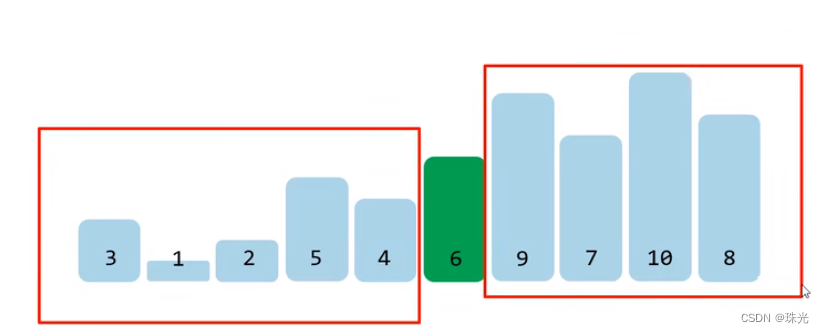
四、快速排序

public static void main(String[] args) {
        int[] arr = {5, 2, 7, 3, 9, 1};
        int[] arrs = quickSort(arr, 0, 5);
        System.err.println(Arrays.toString(arrs));
    }

    /**
     * 快速排序
     *
     * @param arr
     */
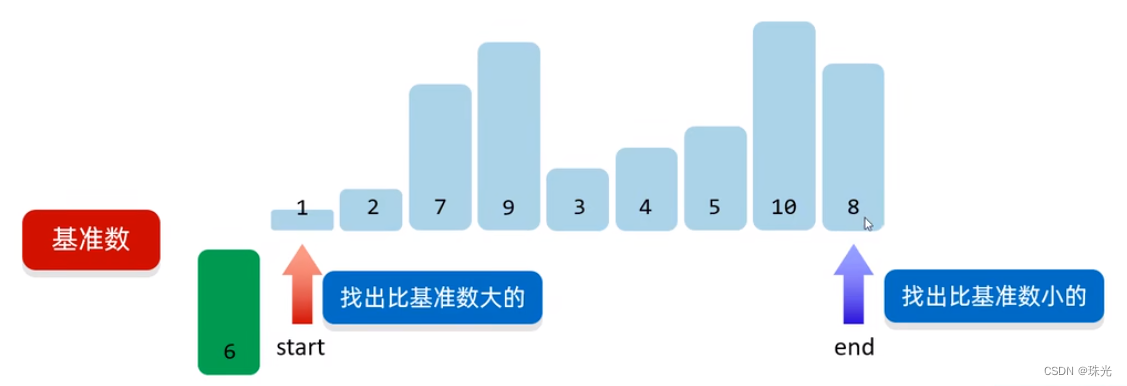
    private static void quickSort(int[] arr, int left, int right) {
        if (left < right) {
            int start = left;
            int end = right;
            int key = arr[left];
            while (start < end) {
            	// 右侧结点比key大，下标左移，一直找到比key小的数
                while (arr[end] > key) {
                    end--;
                }
                // 左侧结点比key大，下标右移， 一直找到比key大的数
                while (arr[start] < key) {
                    start++;
                }
                if (arr[start] == arr[end]) {
                    start++;
                } else {
                    int temp = arr[start];
                    arr[start] = arr[end];
                    arr[end] = temp;
                }
            }
            quickSort(arr, left, start - 1);
            quickSort(arr, end + 1, right);
        }
    }

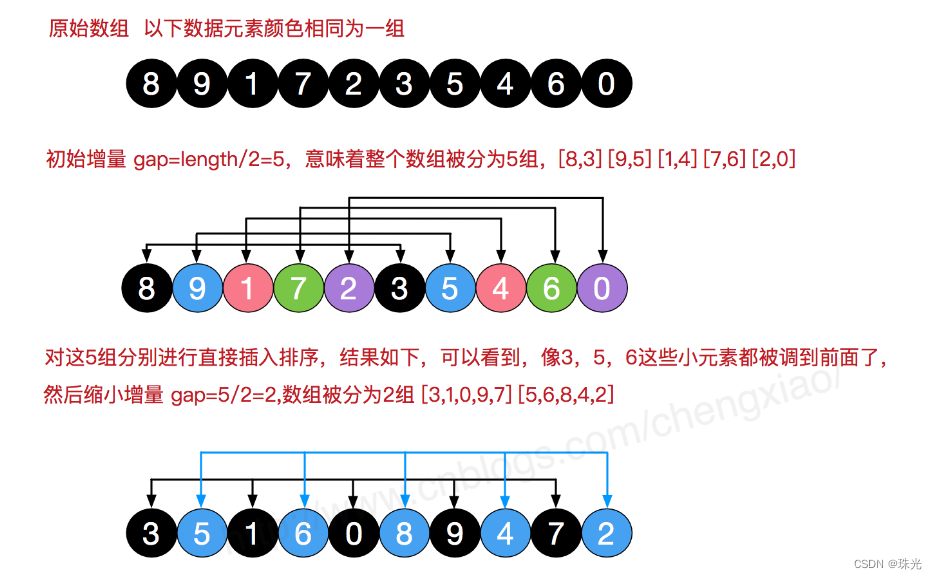
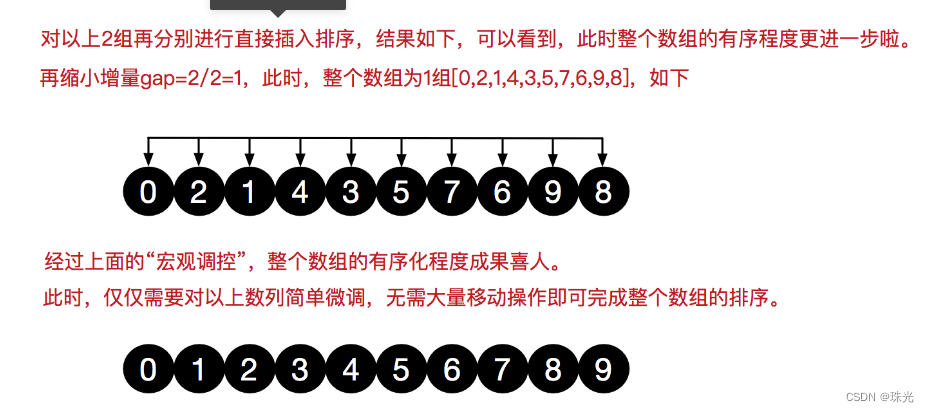
五、希尔排序

    //希尔排序
    public static void shellSort(int[] arr) {
        //遍历所有的步长
        for (int gap = arr.length / 2; gap > 0; gap = gap / 2) {   // gap = 5
            //遍历所有的元素
            for (int i = gap; i < arr.length; i++) {  // i=5
                //遍历本组中所有元素
                for (int j = i - gap; j >= 0; j -= gap) { //j = 0; j=j-gap
                    //如果当前元素大于 加上步长后的那个元素
                    if (arr[j] > arr[j + gap]) {
                        int temp = arr[j];
                        arr[j] = arr[j + gap];
                        arr[j + gap] = temp;
                    }
                }
            }
            //打印每次排序后的结果
            System.out.println(Arrays.toString(arr));
        }

    }

六、归并排序

归并排序：是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用。

public class MergeSort {

    /**
     * 归并排序
     *
     * @param array 待排序的数组
     */
    public static void mergeSort(int[] array) {
        if (array == null || array.length < 2) {
            return;
        }

        // 进行归并排序
        sort(array, 0, array.length - 1);
    }

    /**
     * 对数组进行归并排序
     *
     * @param array 待排序的数组
     * @param left  排序的左边界
     * @param right 排序的右边界
     */
    public static void sort(int[] array, int left, int right) {
        if (left >= right) {
            return;
        }
        int mid = (right +left) / 2 // 计算中间位置
        sort(array, left, mid); // 对左半部分进行归并排序
        sort(array, mid + 1, right); // 对右半部分进行归并排序
        merge(array, left, mid, right); // 合并左右两个有序数组
    }

    /**
     * 合并左右两个有序数组
     *
     * @param array 待合并的数组
     * @param left  左半部分的左边界
     * @param mid   中间位置
     * @param right 右半部分的右边界
     */
    public static void merge(int[] array, int left, int mid, int right) {
        int[] tmp = new int[right - left + 1]; // 临时数组
        int i = left, j = mid + 1, k = 0;
        while (i <= mid && j <= right) { // 依次比较左右两个数组的元素
            if (array[i] <= array[j]) {
                tmp[k++] = array[i++];
            } else {
                tmp[k++] = array[j++];
            }
        }
        while (i <= mid) { // 将左边数组中剩余的元素放入临时数组
            tmp[k++] = array[i++];
        }
        while (j <= right) { // 将右边数组中剩余的元素放入临时数组
            tmp[k++] = array[j++];
        }
        for (int l = 0; l < tmp.length; l++) { // 将临时数组中的元素复制回原数组
            array[left + l] = tmp[l];
        }
    }
}

七、堆排序

大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

public static void heapSort(int[] arr) {
        // 获取数组长度
        int length = arr.length;
        // 获取最后一个非叶子节点下标 ： length / 2 - 1
        for (int i = length / 2 - 1; i >= 0; i--) {
            // 把数组转化为堆，我们称之为建堆
            buildHeap(arr, i, length);
        }
        System.err.println("数组建堆后的结果：{}"+ Arrays.toString(arr));
        // 排序，因为之前已经完成了建堆，意味着，根节点就是我们需要的值
        for (int k = length - 1; k >= 0; k--) {
            // 将当前根节点与未排序的最大子节点进行交换
            swap(arr, 0, k);
            // 剩下的元素继续建堆,要理解i--,刚刚交换的根节点的值就是已排序的不会参与遍历了
            buildHeap(arr, 0, k);
        }
    }

    private static void buildHeap(int[] arr, int i, int length) {
        // 大顶堆的节点调整
        while (true) {
            // 定义最大节点的位置---父节点
            int maxPos = i;
            // 检查在未排序列表中，当前节点的值是不是小于它的左子节点(2i+1)---左节点
            if (i * 2 + 1 < length && arr[i] < arr[i * 2 + 1]) {
                maxPos = i * 2 + 1;
            }
            // 检查在未排序列表中，同时当前的最大节点和i节点的右子节点（2i+2）也比较找出最大值的节点---右节点
            // 也就是找出父节点，左节点，右节点三者中的最大节点值
            if (i * 2 + 2 < length && arr[maxPos] < arr[i * 2 + 2]) {
                maxPos = i * 2 + 2;
            }
            // maxPos没变说明已经找不到比当前节点大的了
            if (maxPos == i) {
                break;
            }
            // 交换两个节点（当前节点和最大值的节点进行交换）
            swap(arr, i, maxPos);
            // 继续往下处理这个过程（）处理调整后，下面的子节点情况
            i = maxPos;
        }
        System.err.println("大顶堆的节点调整后结果：{}"+ Arrays.toString(arr));
    }

    private static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    public static void main(String[] args) {
        int[] arr = new int[]{28, 8, 10, 23, 21, 19, 9};
        System.err.println("要排序的初始化数据：{}"+ Arrays.toString(arr));
        //从小到大排序
        heapSort(arr);
    }

八、计数排序

计数排序是一个排序时不比较大小的排序算法。对于数组里的每个元素来说，如果能知道数组里有多少项小于或等于该元素，就能准确地给出该元素在排序后的数组位置。
数组里所有元素都是正整数。

public static void main(String[] args) {
        int[] arr = {1003,1005,1004,1000,1003,1004,1000,1004};

        countSort(arr);
    }

    private static void countSort(int[] arr) {
        int max = arr[0];
        int min = arr[0];
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
            if (arr[i] < min) {
                min = arr[i];
            }
        }
        int[] numberArr = new int[max - min + 1];

        for (int j = 0; j < arr.length; j++) {
            int num = arr[j] - min;
            numberArr[num]++;
        }

        int index = 0;
        for (int k = 0; k < numberArr.length; k++) {
            for (int n = 0; n<numberArr[k];n++){
                arr[index] = k + min;
                index++;
            }
        }
        System.err.println(Arrays.toString(arr));

    }

九、桶排序

桶排序（Bucket sort）是计数排序算法的升级版，将数据分到有限数量的桶子里，然后每个桶再分别排序

 public static void main(String[] args) {
        int[] arr = {15,8,23,38,28,19,32,21,9};

        bucketSort(arr, 4);

    }

    private static void bucketSort(int[] arr, int size) {
        int max = Integer.MIN_VALUE;
        int min = Integer.MAX_VALUE;

        for (int i = 1; i < arr.length; i++) {
            max = Math.max(max, arr[i]);
            min = Math.min(min, arr[i]);
        }

        //桶编号 =(数组元素 - 最小值) (桶个 - 1) /(最大值 - 最小值)
		// 先查询出二维数组第二列的长度，也就是每个桶放了多少
        int[] bucketSize = new int[size];
        for (int i = 0; i < arr.length; i++) {
            int code = (arr[i] - min) * (size - 1) /(max - min);
            bucketSize[code]++;
        }
		// 定义二维数组
        int[][] bucket = new int[size][];
        for (int code = 0; code < size; code++) {
            bucket[code] = new int[bucketSize[code]];
        }
		// 向二维数组赋值
        int[] bucketSize2 = new int[size];
        for (int number : arr) {
            int code = (number - min) * (size - 1) / (max - min);
            bucket[code][bucketSize2[code]] = number;
            bucketSize2[code]++;
        }
		// 每个桶冒泡排序
        for (int n = 0; n < bucket.length; n++) {
            int[] midArr = bubbleSort(bucket[n]);
            bucket[n] = midArr;
        }

        // 遍历桶，得到排序后结果
        int index = 0;
        int[] sortArr = new int[arr.length];
        for (int t = 0; t < bucket.length; t++) {
            for (int m = 0; m < bucketSize[t]; m++) {
                sortArr[index] = bucket[t][m];
                index++;
            }
        }

        for (int i : sortArr) {
            System.err.print(i + " ");
        }


    }

    private static int[] bubbleSort(int[] arr) {
        //确定排序多少次，总长度-1
        for (int i = 0; i < arr.length - 1; i++) {
            // 每一轮排序，从0开始比较，两两比较；每过一轮，去除末尾数，不进行比较
            // -1是为了防止索引越界
            for (int j = 0; j < arr.length - 1 - i; j++) {
                if (arr[j] > arr[j+1]) {
                    // 交换位置
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
        }
        return arr;
    }

    public static void bucketsort(int[] arr, int bucketSize) {
        // 初始化最大最小值
        int max = Integer.MIN_VALUE;
        int min = Integer.MAX_VALUE;
        // 找出最小值和最大值
        for (int num : arr) {
            max = Math.max(max, num);
            min = Math.min(min, num);
        }

        // 创建bucketSize个桶
        List<List<Integer>> bucketList = new ArrayList<>();
        for (int i = 0; i < bucketSize; i++) {
            bucketList.add(new ArrayList<>());
        }
        // 将数据放入桶中
        for (int num : arr) {
            // 确定元素存放的桶号  //重点
            int bucketIndex = (num - min) * (bucketSize - 1) / (max - min);
            List<Integer> list = bucketList.get(bucketIndex);
            list.add(num);
        }
        // 遍历每一个桶
        int arrIndex = 0;
        for (int i = 0; i < bucketList.size(); i++) {
            List<Integer> list = bucketList.get(i);
            list.sort(null);
            // 对每一个桶排序
            for (int value : list) {
                arr[arrIndex++] = value;
            }
        }
        for (int i : arr) {
            System.err.print(i + " ");
        }
    }

十、基数排序

基数排序不支持负数，想要使用，需要整体增加最小值的绝对值，变成正数，排序后，再减

public static void main(String[] args) {
        int[] arr = {53, 3, 542, 0, 748, 14, 214};
        radixSort(arr);
    }

    private static void radixSort(int[] arr) {
        int max = arr[0];
        for (int k = 0; k < arr.length; k++) {
            if (arr[k] > max) {
                max = arr[k];
            }
        }
        int maxLength = (max + "").length();
        for (int t = 0; t < maxLength; t++) {
            int[][] bucket = new int[10][arr.length];
            int[] wsBucket = new int[10];

            int divide = (int) Math.pow(10, t);
            for (int i = 0; i < arr.length; i++) {
                int ws = arr[i] / divide % 10;
                bucket[ws][wsBucket[ws]] = arr[i];
                wsBucket[ws]++;
            }

            int index = 0;
            for (int m = 0; m < wsBucket.length; m++) {
                if (wsBucket[m] != 0) {
                    for (int k = 0; k < wsBucket[m]; k++) {
                        arr[index] = bucket[m][k];
                        index++;
                    }
                }
            }
            System.err.println(Arrays.toString(arr));
        }

    }