您现在的位置是:首页 >技术交流 >毫米波雷达(mmWave)基本原理网站首页技术交流
毫米波雷达(mmWave)基本原理
1. 引言
毫米波(mmWave)是一种特殊的雷达技术,它使用短波长的电磁波。雷达系统发射电磁波信号,然后其路径上的物体将它反射回去。通过捕捉反射信号,雷达系统可以确定目标的距离、速度和角度。毫米波雷达发射的信号波长在毫米范围内。这被认为是电磁波谱中的短波长,是该技术的优点之一。实际上,处理毫米波信号所需的天线等系统组件的尺寸很小。短波长的另一个优点是精度高。工作在 76-81 GHz(相应波长约为 4 毫米)的毫米波系统将能够检测到小到 1 毫米的运动。一个完整的毫米波雷达系统包括发射(TX)和接收(RX)射频(RF)组件;如时钟这样的模拟元件;如模数转换器(ADC)、微控制器(MCU)和数字信号处理器(DSP)这样的数字元件。以前,这些系统采用离散元件实现,这增加了功耗和整体系统成本。由于系统的复杂性和高频率,系统设计具有挑战性。Texas Instruments (TI) 已经解决了这些挑战,并设计了基于互补金属氧化物半导体(CMOS)的毫米波雷达器件,该器件集成了 TX-RF 和 RX-RF 、模拟组件(如时钟)以及数字组件(如 ADC、MCU 和硬件加速器)。TI 毫米波传感器产品组合中的一些系列集成了 DSP ,来提供额外的信号处理功能。TI 实现了一种特殊的毫米波技术,称为调频连续波(FMCW)。顾名思义, FMCW 雷达连续发射调频信号,以测量距离、角度和速度。这与传统的脉冲雷达系统不同,后者周期性地发射短脉冲。
2. 测距
雷达系统的基本概念是物体在其路径上反射的电磁信号的传输。在 FMCW 雷达使用的信号中,频率随时间线性增加。这种类型的信号也被称为 chirp 。下图显示了 chirp 信号 A-t 函数表示。
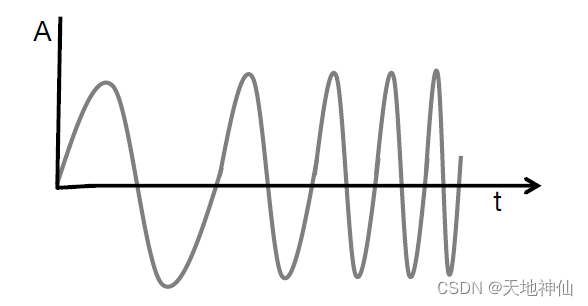
下图也显示了 chirp ,频率是时间的函数。chirp 的特征是起始频率(fc),带宽(B)和持续时间(Tc)。chirp 的斜率(S)捕获频率的变化率。其中 fc = 77 GHz, B = 4 GHz, Tc = 40 μs, S = 100 MHz/μs
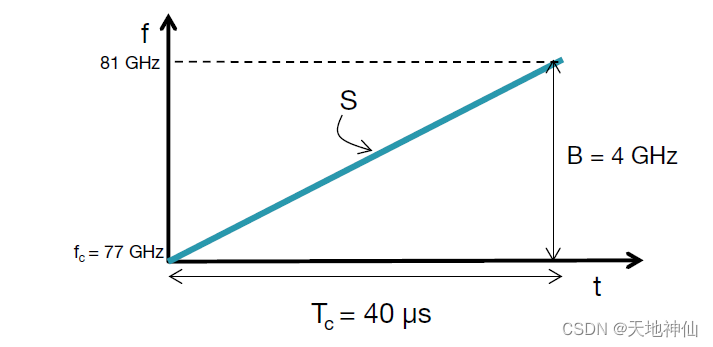
FMCW 雷达系统发送 chirp 信号并捕获其路径上物体反射的信号。
下图是FMCW雷达主要射频组件的简化框图。
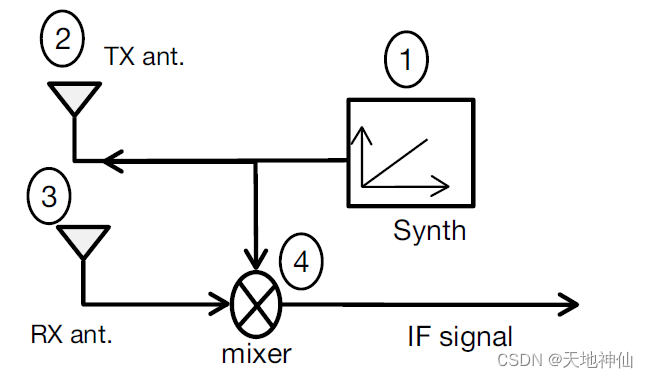
雷达的工作原理如下:
- 合成器产生 chirp
- chirp 由发射天线(TX ant)发射出去
- 物体对 chirp 的反射产生被接收天线捕获的反射 chirp (RX ant)
- 混频器(mixer)结合 RX 和 TX 信号产生中频(IF)信号
频率混频器是一种电子元件,它将两个信号组合在一起,产生一个具有新频率的新信号
对于输入的两个正弦信号 x 1 x_1 x1 和 x 2 x_2 x2
x 1 = s i n ( ω 1 t + Φ 1 ) x_1 = sin(omega_1t+varPhi_1) x1=sin(ω1t+Φ1)(1)
x 2 = s i n ( ω 2 t + Φ 2 ) x_2 = sin(omega_2t+varPhi_2) x2=sin(ω2t+Φ2)(2)
输出 x o u t x_{out} xout的瞬时频率等于两个输入正弦波的瞬时频率之差。输出 x o u t x_{out} xout的相位等于两个输入信号的相位差:
x o u t = s i n [ ( ω 1 − ω 2 ) t + ( Φ 1 − Φ 2 ) ] x_{out}=sin[(omega_1-omega_2)t+(varPhi_1-varPhi_2)] xout=sin[(ω1−ω2)t+(Φ1−Φ2)](3)
混频器的操作也可以通过查看 TX 和 RX 的 chirp 频率和关于时间的函数来图形化地理解。
下图中的上图显示了检测到的单个对象的 TX 和 RX chirp 作为时间的函数。注意,RX chirp 是TX chirp 的延时版本。
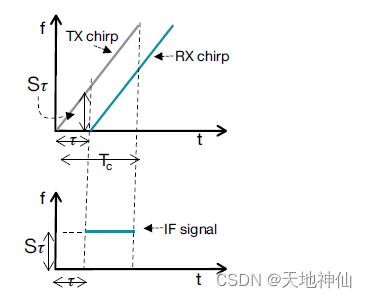
时间延迟(t)可以由下式推导出
τ = 2 d c au=frac {2d} c τ=c2d(4)
d是到被探测物体的距离,c是光速
为了得到混频器输出的中频信号关于时间的函数表示,减去下图上半部分所示的两条线,两条线之间的距离是固定的,这意味着中频信号由一个频率恒定的音调组成。中频信号仅在 TX chirp 和 RX chirp 重叠的时间间隔内有效(即下图中垂直虚线之间的间隔)。混频器输出信号关于时间和幅值函数是正弦波,因为它具有恒定的频率。

中频信号的初始相位( Φ 0 varPhi_0 Φ0)是中频信号开始时对应的时间瞬间(即上图中左侧垂直虚线所表示的时间瞬间)TX chirp 的相位与RX chirp 的相位之差(如下式):
Φ 0 = 2 π f c τ varPhi_0 = 2pi f_c au Φ0=2πfcτ(5)
更进一步的可以被推导为下式
Φ 0 = 4 π d λ varPhi_0 = frac {4 pi d} lambda Φ0=λ4πd(6)1
综上所述,对于距离雷达d处的目标,中频信号为如下式的正弦波
A s i n ( 2 π f 0 t + Φ 0 ) Asin(2pi f_0 t+varPhi_0) Asin(2πf0t+Φ0)(7)2
其中: f 0 = S 2 d c f_0 = frac {S2d} c f0=cS2d, Φ 0 = 4 π d λ varPhi_0 = frac {4 pi d} lambda Φ0=λ4πd
目前的假设是雷达只探测到一个物体。让我们分析一个检测到多个对象的情况。下图显示了从不同对象接收到的三种不同的 RX chirp 。每个 chirp 的延迟时间与与目标的距离成正比。不同的 RX chirp 转换成多个中频信号,每个频率恒定。
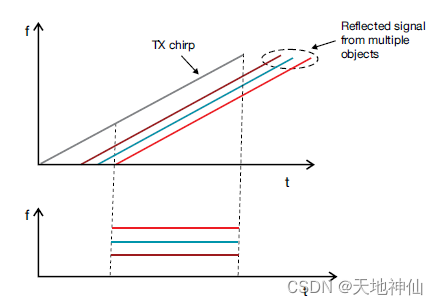
这个由多个信号组成的中频信号必须使用傅里叶变换进行处理,以便分离不同的信号。傅里叶变换处理产生的频谱将会对不同的信号产生不同的峰值,每一个峰值都表示了一个特定距离的物体
2.1 距离分辨率
3. 测速
在本节中,让我们使用相量符号(距离,角度)表示复数。
3.1 双 chirp 测速
为了测量速度,FMCW 雷达发送两个
T
c
T_c
Tc 间隔的 chirps 。每个反射的 chirp 经过 FFT 处理来检测目标的范围(range- FFT),每个 chirp 对应的 range-FFT 在相同的位置有峰值,但相位不同。测量到的相位差对应于
v
T
c
vTc
vTc 物体的运动。
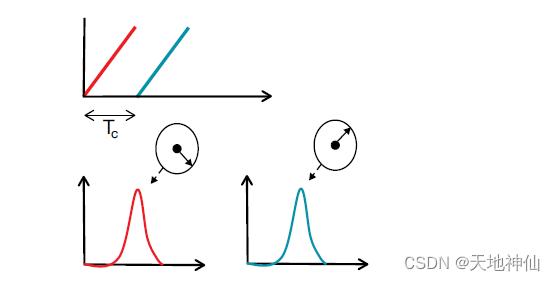
由(6)可得相位差如下式:
Δ Φ = 4 π v T c λ DeltavarPhi = frac {4 pi v T_c } lambda ΔΦ=λ4πvTc(10)
可以推导出速度如下式
v = λ Δ Φ 4 π T c v = frac {lambda Delta varPhi} {4pi T_c} v=4πTcλΔΦ(11)
由于速度测量是基于相位差的,只有当 ∣ Δ Φ ∣ < π mid{Delta varPhi }mid <pi ∣ΔΦ∣<π时,这个测量结果才是准确的,根据(11)我们可以从数学上推导出 v < λ 4 T c v<frac {lambda} {4T_c} v<4Tcλ
式12给出了两个间隔为 T c T_c Tc的 chirp 测量的最大相对速度 V m a x V_{max} Vmax,更快的 V m a x V_{max} Vmax 需要更短的 chirp 间隔时间
v m a x = λ 4 T c v_{max}=frac {lambda} {4T_c} vmax=4Tcλ(12)
3.2 同一范围内多个物体的速度测量
如果在测量时有多个不同速度的运动物体,且它们与雷达的距离相同,则双 chirp 测速方法无法工作。由于这些物体处于相同的距离,它们将产生具有相同中频频率的反射 chirp 。因此 range-FFT将产生单峰,它代表来自所有这些等距离对象的组合信号。简单的相位比较技术是行不通的。
在这种情况下,为了测量速度,雷达系统必须发射两个以上的 chirp。它传输一组N个等间隔的 chirp。这组 chirp 称为 chirp frame。下图显示了chirp frame 的频率与时间的关系。
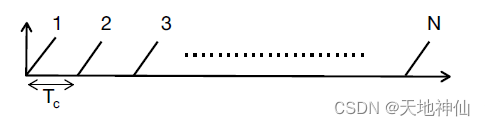
下面以与雷达等距离但速度分别为
v
1
v_1
v1 和
v
2
v_2
v2 且不相等的两个物体为例来描述处理过程。
Range-FFT处理反射的一组 chirp ,产生一组 N 个位置相同的峰值,但每个峰值具有不同的相位,其中包含来自这两个对象的相位(下图中每个对象的单个相位由红色和蓝色相量表示)。
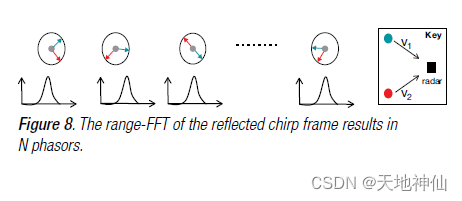
在N个相量上执行第二个FFT,称为 Doppler-FFT,以解析两个对象,如下图所示。
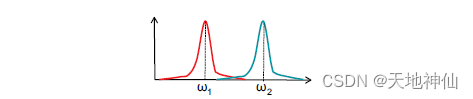
ω 1 omega_1 ω1和 ω 2 omega_2 ω2对应于各自对象连续 chirp 的相位差,如下式
v 1 = λ ω 1 4 π T c v_1 = frac {lambda omega_1} {4pi T_c} v1=4πTcλω1, v 2 = λ ω 2 4 π T c v_2 = frac {lambda omega_2} {4pi T_c} v2=4πTcλω2(13)
3.3 速度分辨率
4.测角
4.1 估算角度
FMCW 雷达系统可以估算出反射信号与水平面的夹角,如下图所示。这个角度也称为 angle of arrival (AoA)。
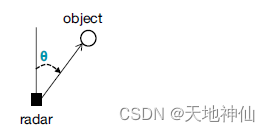
估算角度是基于观察到物体距离的微小变化会导致 range-FFT 或 Doppler-FFT 峰值的相位变化。该结果用于执行角度估计,使用至少两个RX天线,如下图所示。从物体到每个天线的差分距离导致FFT峰值的相位变化。相位变化让我们可以估计AoA。
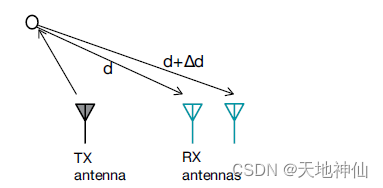
在这种情况下,相位变化的数学表达式为下式
Δ Φ = 2 π Δ d λ DeltavarPhi = frac {2piDelta d} lambda ΔΦ=λ2πΔd(15)
在平面波前的基本几何假设下, Δ d = l s i n ( θ ) Delta d=lsin( heta) Δd=lsin(θ),其中 l 为天线之间的距离。因此,AoA( θ heta θ)可以通过下式使用 Δ Φ DeltavarPhi ΔΦ来计算得到。
θ = s i n − 1 ( λ Δ Φ 2 π l ) heta = sin^{-1}(frac {lambdaDeltavarPhi} {2pi l}) θ=sin−1(2πlλΔΦ)(16)
注意, Δ Φ Delta varPhi ΔΦ 取决于 s i n ( θ ) sin( heta) sin(θ)。这被称为非线性依赖关系。只有当 θ heta θ 的值很小的时候时才有 s i n ( θ ) sin( heta) sin(θ) ~ θ heta θ, s i n ( θ ) sin( heta) sin(θ)才近似为线性函数。
因此,估计精度依赖于AoA,当θ值较小时,估计精度更高。如下图所示。

4.2 最大视场角
雷达的最大视场角由雷达所能估计的最大AoA来确定。如下图
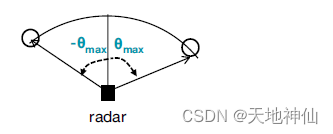
无误差的角度测量要求
∣
Δ
ω
∣
<
π
midDelta omegamid<pi
∣Δω∣<π。根据(16)相当于是
2
π
l
s
i
n
(
θ
)
λ
<
π
frac {2 pi lsin( heta)} lambda < pi
λ2πlsin(θ)<π
由下式可知,间隔的两根天线所能探测的最大视场为
θ m a x = s i n − 1 ( λ 2 l ) heta_{max} = sin^{-1}(frac lambda {2l}) θmax=sin−1(2lλ)(17)
当两根天线之间的间距为 l = λ / 2 l=lambda/2 l=λ/2时,最大视场角为 ± 90 ° pm90° ±90°。
参考文章:
[1]The fundamentals of millimeter wave radar sensors (Rev. A) 点我下载






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结