您现在的位置是:首页 >技术交流 >Unity 四元数网站首页技术交流
Unity 四元数
前言:在场景中,可以用旋转工具改变物体角度,也可以在Inspector窗口中改变物体的X、Y、Z值(欧拉角)来改变物体角度。
虽然用欧拉角表示角度和旋转,但一般人想不到,物体在三维空间的旋转并不是一个简单问题,用3个角度表示是远远不够的
一、万向节锁定
要说明三维物体旋转的复杂性,从"万向节锁定"这一问题入手最有说服力。
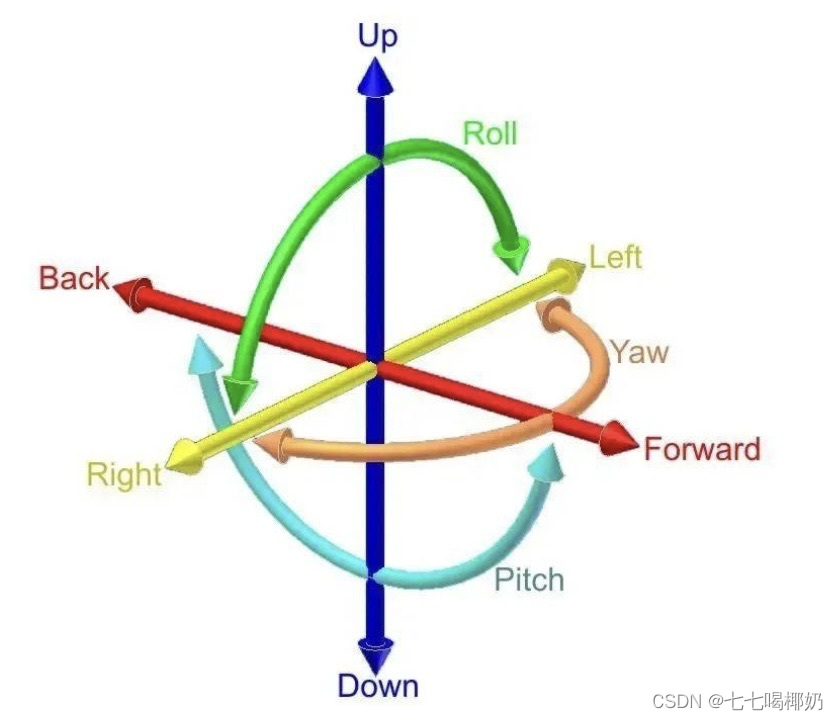
上图为欧拉角示意图。虽然可以调整欧拉角到任意角度,但欧拉角的3个轴并不是独立的,x,y,z轴之间存在嵌套结构,如上图所示,这种嵌套结构被称为"万向节",意思是可以旋转到任意角度的关节。
当中层轴旋转时,会带动内层的轴跟着旋转。通常三维软件的欧拉角,从外层到哪层是按照y->x->z轴的顺序,也就是说x轴的旋转会影响z轴
这里介绍一下用Unity怎样让万向节锁定
- 在场景中新建一个Cube
- 用鼠标在Inspector窗口中朝向的x、y、z这三个字母上拖拽,不要在场景中用鼠标直接旋转物体,这样可以看到3个轴分别是如何旋转的
- 将x的旋转改为90,y和z的旋转改为0
- 用鼠标在旋转的y和z上拖拽,修改y和z的旋转。这是会发现,绕y和绕z旋转方向变成一样了,缺少了一个自由度
按照上述步骤操作,会顺利进入"万向节锁定"状态。一旦进入此状态,物体旋转就会受限制。如果游戏系统是基于欧拉角设计的,那么在主角会俯仰运动的游戏,万向节锁定问题会显得非常严重,而且在其他类型有种也会带来各种问题。
值得说明的是,Unity内部使用四元数比哦时物体的旋转,这里并不会真的遇到锁定问题,只是在编辑器界面上模拟了万向节锁定的效果。
如果用循转工具在场景里直接旋转物体,就跳过了编辑窗口的限制,物体仍然可以自由旋转
到这里,你们可能还没有完全理解3D旋转的奥秘哦,但它具有的复杂性已经毋庸置疑了。幸运的事,数学家哈密顿提出的"四元数"能够让我们跨越欧拉角,彻底解决旋转难题
二、四元数的概念
四元数包含一个标量分量和一个三维向量分量,四元数Q可以记作:
Q=[w,(x,y,z)]。
下面给出四元数的公式定义。对于旋转轴为n,旋转角度为ß的旋转,如果用四元数表示,则四个分量分别为:
- w=cos(ß/2)
- x=sin(ß/2)cos(∂x)
- y=sin(ß/2)cos(∂y)
- z=sin(ß/2)cos(∂z)
用四元数表示旋转一旦也不知管,4个分量w、x、y、z与绕各轴的旋转角度并没有直接的对应关系。在实际开发中也不要试图获取和修改某一份量,应当只做整体处理。
前文提到,矩阵也可以表示旋转,而且矩阵也不存在万向节锁定的问题。其实,旋转还可以用欧拉角和四元数表示,但么一种都有自己的优缺点,下面对这三种方式进行对比
|
| 欧拉角 | 矩阵 | 四元数 |
| 旋转一个位置点 | 不支持 | 支持 | 不支持 |
| 增量旋转 | 不支持 | 支持,运算量大 | 支持,运算量小 |
| 平滑差值 | 支持(存在问题) | 基本不支持 | 支持 |
| 内存占用 | 3个浮点数 | 16个数值 | 4个浮点数 |
| 表达式是否唯一 | 无数种 | 唯一 | 互为负的两种表示 |
| 潜在问题 | 欧拉角锁定 | 矩阵蠕变 | 误差累计 |
实际应用中应根据优缺点来应用,并尽可能在引擎层面进行统一,尽量减少开发时的问题
小提示:Unity内部旋转使用四元数,即结构体Quaternion表示的,但在街面上很多地方会转为更直观的偶来奥,以便直接指定旋转的角度,这种方式兼顾了准确性和便利性
三、Quaternion结构体
这部分介绍Quaternion的属性和方法
属性:
| 属性 | 说明 |
| x | 四元数x的分量,不应直接修改 |
| y | 同x |
| z | 同x |
| w | 同x |
| this[int index] | 允许通过下标运算符访问x、y、z、w分量。例如[1]可以访问y |
| eulerAngles | 获得对应的欧拉角 |
| identity | 获得无旋转的四元数 |
方法和运算符:
| 方法 | 说明 |
| ToAngleAxis | 将旋转转换为一个轴和一个角度的形式 |
| SetFromToRotation | 与FromToRotation类似,但是直接修改当前四元数对象 |
| SetLookRotation | 与LookRotation类似,但是直接修改当前四元数对象 |
| * | 四元数相乘,代表依次旋转的操作 |
| == | 判断四元数是否相等 |
| != | 判断四元数是否不等 |
| Dot | 两个旋转点乘 |
| AngleAxis | 根据一个轴和角度获得一个四元数 |
| FromToRotation | 获得一个四元数,代表从from到to向量的旋转 |
| LookRotation | 给定前方和上方向量,获得一个旋转 |
| Slerp | 插值,根据比例在两个四元数之间进行球面插值 |
| Lerp | 插值,根据比例在两个四元数之间进行插值并将结果规范化 |
| RotateTowards | 将旋转from变到旋转to |
| Inverse | 返回四元数的逆 |
| Angle | 返回两个旋转之间的夹角 |
| Euler | 转换为对应的欧拉角 |
四、理解和运用四元数
在前文中,详细介绍了"位置"与"向量"的区别。下面引出与之对应的另一对概念——"朝向"与"旋转"。
朝向和位置都是一种状态,旋转和向量指的是变化量
位置和向量都用Vector3表示,位置和朝向都用四元数表示
理解了Vector3加法的意义,就可以类比出四元数的旋转操作,只是加法变成了乘法
下表列出四元数乘法的含义
| 元素1 | 运算符 | 元素2 | 一般含义 |
| 朝向 | * | 朝向 | 意义不明 |
| 朝向 | * | 旋转 | 从某个朝向开始,旋转一个角,得到新的朝向 |
| 旋转 | * | 旋转 | 组合两次旋转,得到合并的结果 |
与向量不同的是,四元数相乘不满足交换律,这也印证了三维空间中物体的旋转不是一个简单的问题。
有意思的是,四元数乘法可以直接作用于向量,这样就可以方便地旋转向量了:
旋转*向量:将向量旋转一个角,得到新的向量
注意:四元数乘以向量时,必须四元数在前,向量在后。
五、四元数的插值
前文通过介绍"万向节锁定",解释了使用四元数的必要性,其实四元数还有另一个大用,就是做动画与插值。
物体的转向动画应该是直接的、均匀的,不能给人"绕远"的感觉。
几何上,在球面上的两点之间移动,沿"大圆"的路径是最短的。大圆的定义是"过球心的平面与球面相交形成的圆",换句话说就是能在球面上画出的最大的那一类圆。
两个朝向之间的旋转动画,当旋转的路径符合大圆时,旋转路径是最短的,看起来也最舒服。
欧拉角在制作旋转动画时具有很大缺陷。如果旋转较为复杂,x、y、z轴都有旋转时,物体不会按照"大圆"的路径运动,得到的结果会很奇怪。矩阵在表现旋转动画时,也很难计算正确的插值点。
而四元数就很擅长插值运算。Unity提供了Quaternion.Slerp()方法,用于旋转的插值。其函数定义如下
Static Quaternion Slerp(Quaternion a,Quaternion b,float t);//t取0到1之间的值
六、朝向与向量
朝向代表空间中的一个方向,而向量也可以表示一个方向,因此有时也可以用向量直接表示物体的朝向。
我们不仅可以通过transform.forward属性获得只想物体前方的单位向量,而且可以直接设置它以改变物体的朝向。
向量可以代表朝向,四元数也可以代表朝向,那么向量也就可以转化为四元数。向量转化为四元数的方法定义如下:
Quaternion Quaternion.LookRotation(Vector3 forward) ;
Quaternion Quaternion.LookRotation(Vector3 forward,Vector3);
Quaternion.LookRotation提供了直接获得朝向的一种方法。
仔细思考会发现——难道四元数可以用向量代替吗?应该不行,如果能替代还要四元数干啥。其实向量有很大的局限性,例如,一个人躺在床上,面朝上,前方是世界坐标系上方,这时,他可以在保持面朝上的情况下在床上水平旋转,让头部朝东朝西。而无论头朝哪里,前方都可以保持向上。
这说明了代表某个向量方向的四元数不是唯一的。如果只用一个向量代表前方,理论上有无数种四元数都指向该方向,但它们的"上方"不同。如果仅指定前方,即使使用LookRotation方法只有一个参数的形式,Unity也会用某种规则假定一个合适的"上方";而如果要精确地控制,则要用Quaternion的另一种形式,用两个参数分别制定前方向量和上方向量,这样就可以得到更符合要求的结果






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结