您现在的位置是：首页 >技术教程 >深入理解2D卷积和3D卷积网站首页技术教程

在项目中用到了conv3但是对其背后的原理还有一些模糊的地方，conv2d与多通道的conv2d的区别在哪里？conv3d的思想理论是什么？对此进行探究和记录…
首先要明确多通道的2d卷积和3d卷积是不一样的，3d是可以在通道中移动的，2d不可以

卷积核的维度

卷积核的维度指的的进行滑窗操作的维度，而滑窗操作不在channel维度上进行，不管有几个channel，它们都共享同一个滑窗位置（虽然2D多channel卷积的时候每个channel上的卷积核权重是独立的，但滑窗位置是共享的）。所以在讨论卷积核维度的时候，是不把channel维加进去的。

2D conv的卷积核就是$(c,k_h,k_w)$，因此，对于RGB图像做2D卷积，卷积核可以是conv2D(3,3) 而不该是conv3D(3,3,3)；

3D conv的卷积核就是$(c,k_d,k_h,k_w)$，其中k_d就是多出来的第三维，根据具体应用，在视频中就是时间维，在CT图像中就是层数维.

2D卷积

单通道

首先了解什么是卷积核，卷积核(filter)是由一组参数构成的张量，卷积核相当于权值，图像相当于输入量，卷积的操作就是根据卷积核对这些输入量进行加权求和。我们通常用卷积来提取图像的特征。

直观理解如下：下图使用的是 3x3卷积核(height x width,简写 $H\times W$ )的卷积，padding为1(周围的虚线部分，卷积时为了使卷积后的图像大小与原来一致，会对原图像进行填充)，两个维度上的strides均为1(滑动步长，这里体现为每次滑动几个小方格)。

针对单通道，输入图像的channel为1，即输入大小为$(1,height,weight)$，卷积核尺寸为 $(1,k_h,k_w)$，卷积核在输入图像上的的空间维度（即(height, width)两维）上进行进行滑窗操作，每次滑窗和 $(k_h,k_w)$ 窗口内的values进行卷积操作（现在都用相关操作取代），得到输出图像中的一个value。

上图是通道数为1的2维图像的卷积操作，静态表示为：

多通道

了解了单通道图像的卷积之后，再来看多通道图像的卷积，我们知道灰度图像只有一个通道，而 RGB 图像有R、G、B三个通道。
多通道图像的一次卷积要对所有通道上同一位置的元素做加权和，因此卷积核的shape变成了 $H\times W\times channels$，没有错卷积核变成了3维，但这不是3维卷积，因为我们区分几维卷积看的是卷积核可以在几个维度上的滑动，卷积核是不能在 channels上滑动的，因为上面提到每次卷积都要关联所有通道上同一位置上的元素。
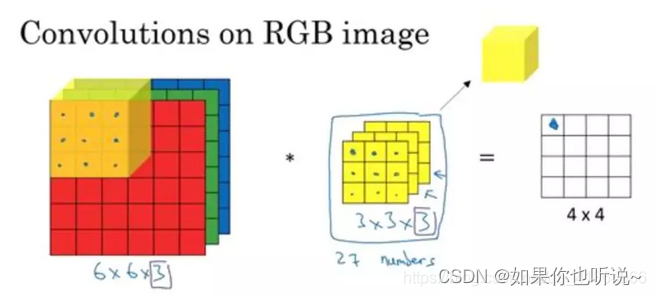
3通道的卷积表示如下：是对每个通道进行2d卷积操作然后把最后的值相加的到右侧的小方块。

上图将3个通道分开表示，卷积核也分开表示，filter1、filter2、filter3均为二维卷积核，堆叠在一起便形成了$H\times W\times 3$ 的卷积核，同样的我们将3个通道也堆叠在一起;

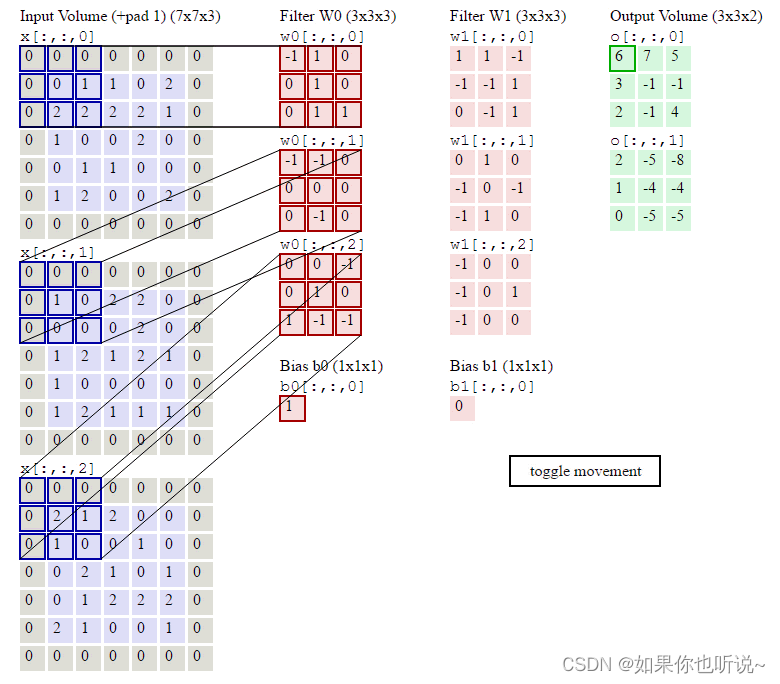
针对多通道，假定输入图像的channel为c，即输入大小为$(c,height,weight)$，卷积核尺寸为 $(c,k_h,k_w)$， 卷积核在输入图像的空间维度即$(height,width)$两维上进行滑窗操作（在channel这一维度没有滑动只有相加），每次滑窗与c个channels上的$ (k_h, k_w)$ 窗口内的所有的values进行相关操作，得到输出图像中的一个value（多通道的信息被完全压缩了)

于是形成了下面的3维表示图：

得到多个Feature Map就需要多个卷积核，下面这个例子是有2个卷积核：

代码

torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)

• in_channels (int) – Number of channels in the input image
• out_channels (int) – Number of channels produced by the convolution
• kernel_size (int or tuple) – Size of the convolving kernel
• stride (int or tuple, optional) – Stride of the convolution. Default: 1
• padding (int, tuple or str, optional) – Padding added to all four sides of the input. Default: 0
• padding_mode (string*,* optional) – 'zeros', 'reflect', 'replicate' or 'circular'. Default: 'zeros'
• dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1
• groups (int, optional) – Number of blocked connections from input channels to output channels. Default: 1
• bias (bool, optional) – If True, adds a learnable bias to the output. Default: True

Applies a 2D convolution over an input signal composed of several input planes.

In the simplest case, the output value of the layer with input size $(N,C_{\text{in}},H,W)$and output $(N,C_{\text{out}},H_{\text{out}},W_{\text{out}})$ can be precisely described as:

$$\text{out}(N_i,C_{{\text{out}}_j})=\text{bias}(C_{{\text{out}}_j})+\sum _{k=0}^{C_{\text{in}}-1}\text{weight}(C_{{\text{out}}_j},k)\star \text{input}(N_i,k)$$

where ⋆ is the valid 2D cross-correlation operator, NN is a batch size, CC denotes a number of channels, HH is a height of input planes in pixels, and WW is width in pixels.

This module supports TensorFloat32.

• stride controls the stride for the cross-correlation, a single number or a tuple.

• padding controls the amount of padding applied to the input. It can be either a string {‘valid’, ‘same’} or a tuple of ints giving the amount of implicit padding applied on both sides.

• dilation controls the spacing between the kernel points; also known as the à trous algorithm. It is harder to describe, but this link has a nice visualization of what dilation does.

• groups controls the connections between inputs and outputs. in_channels and out_channels must both be divisible by groups. For example,

  • At groups=1, all inputs are convolved to all outputs.
  • At groups=2, the operation becomes equivalent to having two conv layers side by side, each seeing half the input channels and producing half the output channels, and both subsequently concatenated.
  • At groups= in_channels, each input channel is convolved with its own set of filters (of size $\frac{\text{out\_channels}}{\text{in\_channels}}$ ).

The parameters kernel_size, stride, padding, dilation can either be:

• a single int – in which case the same value is used for the height and width dimension
• a tuple of two ints – in which case, the first int is used for the height dimension, and the second int for the width dimension

example

# With square kernels and equal stride
m = nn.Conv2d(16, 33, 3, stride=2)
# non-square kernels and unequal stride and with padding
m = nn.Conv2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2))
# non-square kernels and unequal stride and with padding and dilation
m = nn.Conv2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2), dilation=(3, 1))
input = torch.randn(20, 16, 50, 100)
output = m(input)

2d卷积操作后变化

3D卷积

单通道

用类似的方法我们先分析单通道图像的3D卷积，3D卷积的对象是三维图像，因此卷积核变成了$depth imes height imes width $简写为$D imes H imes W $。单通道的3D卷积动态图如下：

针对单通道，与2D卷积不同之处在于，输入图像多了一个 depth 维度，故输入大小为$(1,depth,height,width)$，卷积核也多了一个$k_d$维度，因此卷积核在输入3D图像的空间维度$(depth,height,width)$上均进行滑窗操作，每次滑窗与$(k_d,k_h,k_w)$窗口内的values进行相关操作，得到输出3D图像中的一个value，最终输出一个3D的特征图。

这里的3D不是通道导致的，而是深度（多层切片，多帧视频），因此，虽然输入和卷积核和输出都是3D的，但都可以是单通道的。

将上述静态表示成：

多通道

然后将filter1、filter2、filter3堆叠在一起形成一个4维卷积核$D\times H\times W\times 3$，同理将各通道堆叠在一起就形成了多通道的3D卷积输入图像。

针对多通道,比如c个通道，输入大小为$(c,depth,height,width)$，与2D多通道卷积的操作类似，对于每次滑窗，卷积核同时与c个channels上的 $(k_d,k_h,k_w)$ 窗口内的所有values进行相关操作，得到输出3D图像中的一个value。
由于3D卷积中的卷积核是3D的，因此在每个channel下使用的是同样的参数，权重共享。不同于2D多通道下的卷积核，后者在每一个channel使用的权重是一样的，不同的通道权重可能不一样。

代码

torch.nn.Conv3d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)

• in_channels (int) – Number of channels in the input image
• out_channels (int) – Number of channels produced by the convolution
• kernel_size (int or tuple) – Size of the convolving kernel
• stride (int or tuple, optional) – Stride of the convolution. Default: 1
• padding (int, tuple or str, optional) – Padding added to all six sides of the input. Default: 0
• padding_mode (string*,* optional) – 'zeros', 'reflect', 'replicate' or 'circular'. Default: 'zeros'
• dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1
• groups (int, optional) – Number of blocked connections from input channels to output channels. Default: 1
• bias (bool, optional) – If True, adds a learnable bias to the output. Default: True

和2D卷积函数基本上是一样的，只是维度和内部的工作机制不太一样。

Applies a 3D convolution over an input signal composed of several input planes.

In the simplest case, the output value of the layer with input size$ (N, C_{in}, D, H, W)$ and output $(N,C_{out},D_{out},H_{out},W_{out})$ can be precisely described as:

$$out(N_i,C_{ou{t}_j})=bias(C_{ou{t}_j})+\sum _{k=0}^{C_{in}-1}weight(C_{ou{t}_j},k)\star input(N_i,k)$$

where ⋆ is the valid 3D cross-correlation operator

This module supports TensorFloat32.

• stride controls the stride for the cross-correlation.

• padding controls the amount of padding applied to the input. It can be either a string {‘valid’, ‘same’} or a tuple of ints giving the amount of implicit padding applied on both sides.

• dilation controls the spacing between the kernel points; also known as the à trous algorithm. It is harder to describe, but this link has a nice visualization of what dilation does.

• groups controls the connections between inputs and outputs. in_channels and out_channels must both be divisible by groups. For example,

  • At groups=1, all inputs are convolved to all outputs.
  • At groups=2, the operation becomes equivalent to having two conv layers side by side, each seeing half the input channels and producing half the output channels, and both subsequently concatenated.
  • At groups= in_channels, each input channel is convolved with its own set of filters (of size $\frac{\text{out\_channels}}{\text{in\_channels}}$).

The parameters kernel_size, stride, padding, dilation can either be:

• a single int – in which case the same value is used for the depth, height and width dimension
• a tuple of three ints – in which case, the first int is used for the depth dimension, the second int for the height dimension and the third int for the width dimension