1. 非线性规划 求解局部最优

首先展示一个最简单的示例：

from scipy.optimize import minimize

def fun_convex(x):
    return (x - 1) ** 2 + 3

minimize(fun=fun_convex, x0=0, bounds=[(-10,10)])

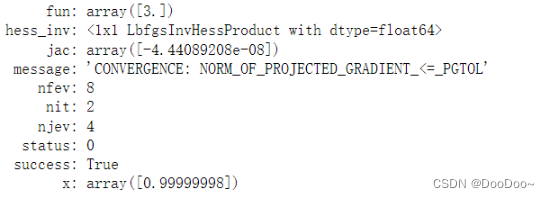
scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)

fun: 求最小值的目标函数
x0: 变量的初始猜测值，如果有多个变量，需要给每个变量一个初始猜测值
args: 常数值，fun中的可变常量
method: 求极值的方法，官方文档给了很多种。一般使用默认
constraints: 约束条件，针对fun中为参数的部分进行约束限制

scipy.optimize.minimizel 官方说明文档
通过scipy.optimize.minimize，我们可以很轻松的求解凸函数的局部最优的数值解，这里有几个注意点：
①求解函数为非凸函数时，所求结果为局部最优
②求解函数为凸函数时，所求结果为最小值
③所求皆为数值解而不是理论解

下面展示一个非凸函数的示例：

from scipy.optimize import minimize

def fun_nonconvex(x): 
    if x<0:
        return ( x + 2 ) ** 2 + 1
    else:
        return ( x - 2 ) ** 2 + 2

minimize(fun=fun_nonconvex, x0=0, bounds=[(-10,10)])

我们可以发现，所求的x=2并非为全局最优解（应该是x=-2）而是局部最优解，所求结果与设置的初值x0有很大关系。

2. 求解全局最优

通过以上内容我们可以发现，scipy.optimize.minimize只能求解局部最优解，那么我们该如何求解全局最优呢？本文介绍scipy.optimize的3种方法：
brute()：网格搜索优化，属于暴力全局优化。 brute官方说明文档
differential_evolution()：差分进化本质上是随机的(不使用梯度方法)来寻找最小值，并且可以搜索大面积的候选空间，但通常需要比传统的基于梯度的技术更多的函数评估。 differential_evolution官方说明文档
basinhopping()：Basin-hopping 是一种two-phase 方法，它将全局步进算法与每一步的局部最小相结合，会在每次随机跳跃后使用局部松弛，旨在模拟原子簇能量最小化的自然过程。 basinhopping官方说明文档

使用蛮力的brute()就不深入探讨，接下来给出differential_evolution()和basinhopping()的简单例程：

from scipy.optimize import differential_evolution, basinhopping

def fun_nonconvex(x): 
    if x<0:
        return ( x + 2 ) ** 2 + 1
    else:
        return ( x - 2 ) ** 2 + 2

res_differential_evolution = differential_evolution(func=fun_nonconvex, bounds=[(-10,10)])
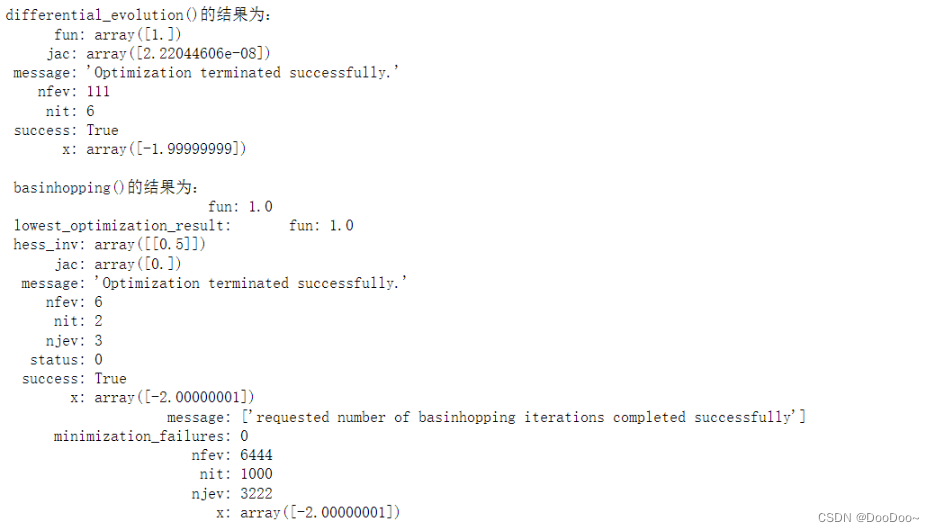
print('differential_evolution()的结果为：
', res_differential_evolution)

res_basinhopping = basinhopping(func=fun_nonconvex, x0=0, niter=1000)
print('
 basinhopping()的结果为：
', res_basinhopping)

这两种方法均可以求得全局最优解：