您现在的位置是:首页 >技术教程 >力扣第 104 场双周赛 2681. 英雄的力量网站首页技术教程
力扣第 104 场双周赛 2681. 英雄的力量
简介力扣第 104 场双周赛 2681. 英雄的力量
原题链接力扣
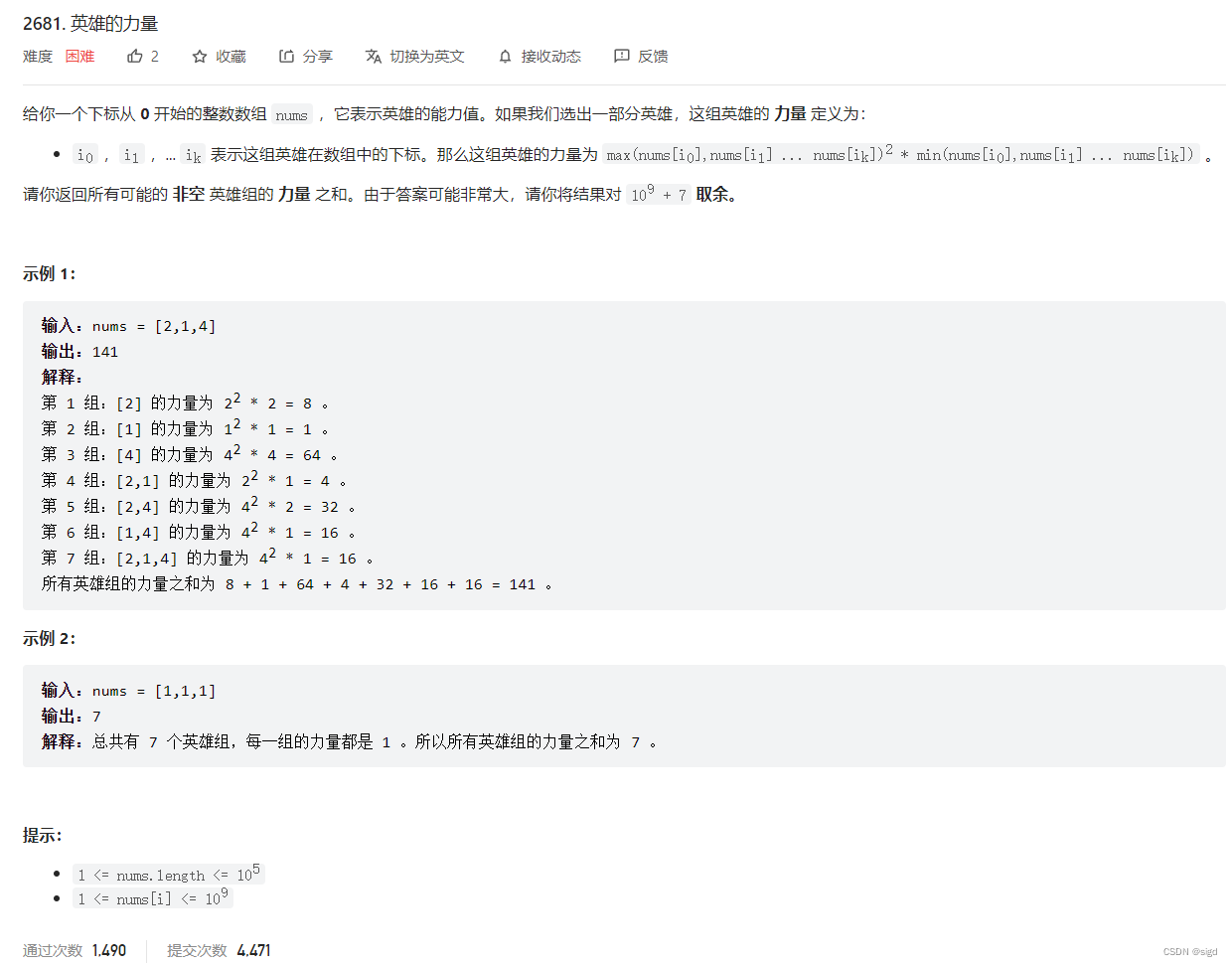
题目大意:我开始看成连续子段了,写了个递归程序.......
一个数组任选一个子序列,子序列的力量值=最大值平方*最小值。求所有子序列的力量和。
分析过程:如序列长度为n,子序列总数为2的n次幂,显然不可能枚举所有子序列来求解。那么只能锁定子序列最大值和最小值来处理。容易想到先排序,排序后的序列可以取任意ai和aj,那么ai最小值,aj 最大值,i和j之间的元素可以任取,例如i=2,j=6,那么i和j之间有3个其他元素,这3个元素可以任取,因此共有2的3次幂共8种选取方法:(a2,a6) (a2,a3,a6) (a2,a4,a6) (a2,a5,a6)(a2,a3,a4,a6).......。枚举所有i和j,时间复杂度为O(n2)。
这类问题如何继续降低复杂度。一般来说都会存在某种规律,使得下一次的处理能利用上一次的结果,也有写问题存在某种(数学)方法,能直接求得解。本题目通过找规律解决。
假设a1为最小值,那么子序列中必然有a1,此时如果锁定ai为最大值,那么所有满足(a1最小,ai最大)的子序列数量必然ai*ai*a1*pow(2,i-2)。
枚举下最大最小值分别为(i,j)的公式
| 最大值j最小值i | a1 | a2 | a3 | ...... | 总和 |
| a2 | a1*a2*a2 | (a1)*a2*a2 | |||
| a3 | 2a1*a3*a3 | a2*a3*a3 | (2a1+a2)*a3*a3 | ||
| a4 | 4a1*a4*a4 | 2a2*a4*a4 | (4a1+2a2+a3)*a4*a4 | ||
| a5 | 8a1*a5*a5 | 4a2*a5*a5 | 2a3*a5*a5 | ...... | (8a1+4a2+2a3+a4)*a5*a5 |
| a6 | 16a1*a6*a6 | 8a2*a6*a6 | 4a3*a6*a6 | ...... | |
可以发现规律为当ai为最大值时,其组成所有子序列的力量和为Y[i]*a[i]*a[i],而这个Y[i]可以由Y[i-1]*2+a[i-1]求得。
class Solution {
public:
int sumOfPower(vector<int>& nums) {
int i,j,r=nums.size()-1,mod=1e9+7;;
sort(nums.begin(),nums.end());/**< 排序 */
long long ans=0,sum=nums[0];
for(i=0;i<=r;i++)/**< 就一个元素序列单独处理 */
ans=(ans+1LL*nums[i]*nums[i]%mod*nums[i])%mod;
for(i=1;i<=r;i++)/**< 最大值为i的力量和 */
{
long long temp=1LL*nums[i]*nums[i]%mod;
ans=(ans+temp*sum%mod)%mod;
sum=(sum*2+nums[i])%mod;/**< i+1的系数 */
}
return (int)ans;
}
};
两个循环综合在一起的写法。
class Solution {
public:
int sumOfPower(vector<int>& nums) {
int i,j,r=nums.size()-1,mod=1e9+7;;
sort(nums.begin(),nums.end());/**< 排序 */
long long ans=0,sum=0;
for(i=0;i<=r;i++)/**< 最大值为i的力量和 */
{
long long temp=1LL*nums[i]*nums[i]%mod;
ans=(ans+temp*(sum+nums[i])%mod)%mod;
sum=(sum*2+nums[i])%mod;/**< i+1的系数 */
}
return (int)ans;
}
};
风语者!平时喜欢研究各种技术,目前在从事后端开发工作,热爱生活、热爱工作。






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结