您现在的位置是：首页 >技术教程 >【差分+操作】C. Helping the Nature网站首页技术教程

Problem - 1700C - Codeforces

题意：

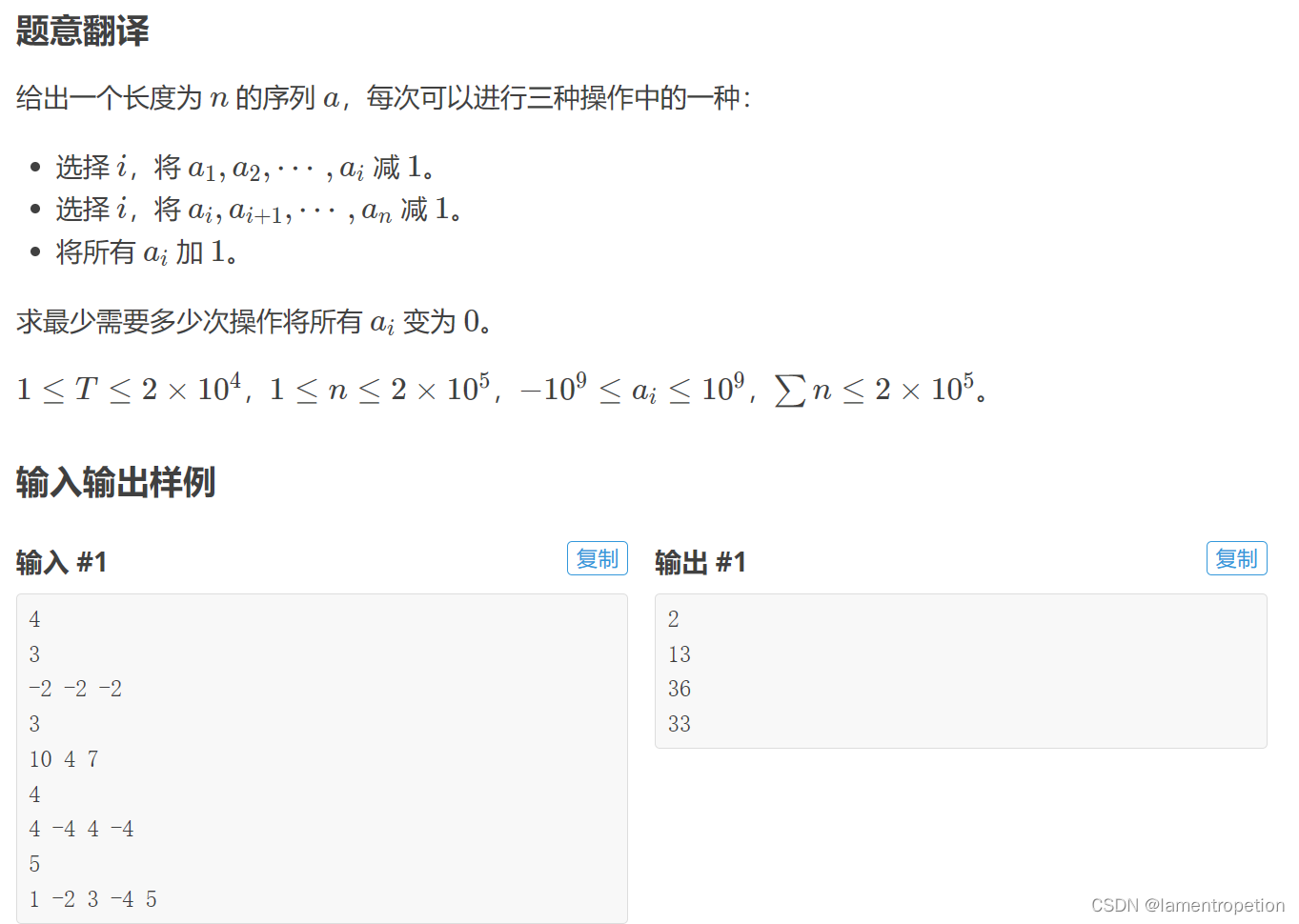
思路：

一开始手玩了一下

如果不是高低高的形式，那么一定不能通过操作3把全部元素变成0

因此就是先把所有元素变成高低高的形式

但是低在什么地方不确定

因此考虑枚举中间低谷位置，O(1)计算贡献

但是不是这么想的

对于区间操作，可以考虑差分数组

把区间操作转化为单点操作

操作1：-1       +1

操作2：           -1

操作3：+1

目的就是把差分数组全部变成0

先把2~N部分变成0

如果d[i]大于0，就考虑操作2

否则考虑操作1，但是操作1会改变d1

因此还需操作3把d1加回去

Code：

#include <bits/stdc++.h>

#define int long long
#define max(a,b) (a>b?a:b)
#define min(a,b) (a<b?a:b)

using i64 = long long;

using namespace std;

const int mxn=2e5+10;
const int mxe=3e5+10;
const int mod=1e9+7;

int N;
int a[mxn],d[mxn];

void solve(){
	cin>>N;
	for(int i=1;i<=N;i++) cin>>a[i],d[i]=a[i]-a[i-1];
	int ans=0,t=0;
	for(int i=2;i<=N;i++){
		if(d[i]<0) t-=d[i];
		else ans+=d[i];
	}
	ans+=t;
	if(t<d[1]) ans+=(d[1]-t);
	else ans+=(t-d[1]);
	cout<<ans<<'
';
}
signed main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int __=1;cin>>__;
    while(__--)solve();return 0;
}