固定效应vs随机效应

参考：统计学中的「固定效应 vs. 随机效应」 - 知乎 (zhihu.com)

FE（固定效应，异质性[非随机]截距）：由于面板数据有个体和时间两个维度，所以FE也分为个体固定、时间固定、双固定。例如个体固定，可以类比于方差分析中把不同组别用虚拟变量来表示。我们可以使用“最小二乘虚拟变量回归法”（Least Square Dummy Variable, LSDV）来分析面板数据，那么在模型估计的时候，LSDV的做法就是给N个个体生成N – 1个0/1虚拟变量，然后将这些虚拟变量与主要的预测变量一起纳入回归方程，做OLS回归（并且常常需要计算cluster稳健标准误），结果中每个虚拟变量的系数就是个体间异质性的截距。时间固定与双固定的做法与之类似。除了LSDV，还可以使用“均值离差法”、“一阶差分法”等做固定效应模型，其中，均值离差法较为常用，其做法是计算出每个个体在T个时间点上的“个体内均值”，然后用原始观测值减去个体内均值进行均值离差校正（相当于做了一个跨时间的组中心化处理；time-demeaning），最后以自变量和因变量的离差值进行回归，分析得到的结果与LSDV基本是一致的。因此总体来看，所谓固定效应FE，就是对面板数据中的不同个体或不同时间做的虚拟变量OLS回归（LSDV）。由于在多数的经济数据中，个体不可观测的异质性截距（ui）往往与解释变量（Xit）有关或相互干扰，FE的这种虚拟变量回归的做法可以很好地控制并排除那些不可观测的个体差异的影响，从而可以在一定程度上解决遗漏变量的问题，提高模型的准确性。

RE（随机效应，异质性[随机]截距）：上面所说的FE允许个体异质性截距 ui 与解释变量 Xit 存在相关；相比之下，RE有着更严苛、也更难满足的假设，即假设 ui 与所有自变量 Xit 均不相关，并且 ui（残差）是一个服从正态分布的随机变量。RE模型也有相应的估计方法，例如可行广义最小二乘法（FGLS）、最大似然法（ML）等。如果使用最大似然法，其结果将与HLM随机截距模型的结果一致。

python实现固定效应模型

使用linearmodels库中的PanelOLS方法或PanelOLS.from_formula方法，所以首先需要安装linearmodels库，我使用的是python3.9的环境，注意python版本3.7无法使用该函数会报错，类似如下：

---------------------------------------------------------------------------
KeyError                                  Traceback (most recent call last)
[<ipython-input-6-538f694ebc58>](https://localhost:8080/#) in <module>
      1 panel_data = generate_panel_data()
----> 2 mod = PanelOLS.from_formula("y ~ x1 + x0 + EntityEffects", panel_data.data)
      3 res = mod.fit(cov_type="clustered", cluster_entity=True)

4 frames
[/usr/local/lib/python3.7/dist-packages/formulaic/parser/types/structured.py](https://localhost:8080/#) in __getitem__(self, key)
    327             return self._structure[key]
    328         raise KeyError(
--> 329             f"This `{self.__class__.__name__}` instance does not have structure @ `{repr(key)}`."
    330         )
    331 

KeyError: 'This `Formula` instance does not have structure @ `1`.

安装完成后，导入该方法，这里使用statsmodels中的Grunfeld数据集进行演示，故导入该数据集，示例代码如下：

from linearmodels.panel import PanelOLS
from statsmodels.datasets import grunfeld
data = grunfeld.load_pandas().data
data = data.set_index(["firm","year"])
grunfeld_fe = PanelOLS.from_formula("invest ~ value + capital + EntityEffects + TimeEffects", data=gf)                          
print(grunfeld_fe.fit())

使用固定效应模型一定要重新设置索引，且必须设置两个，（否则会报错：ValueError: The index on the time dimension must be either numeric or date-like）无论是使用时间固定效应还是个体固定效应或双固定效应，这里指定firm和year列为新的索引，另外PanelOLS.from_formula中的EntityEffects和TimeEffects分别指定个体固定效应和时间固定效应，两者都包含在参数中则表示双固定效应模型。结果如下：

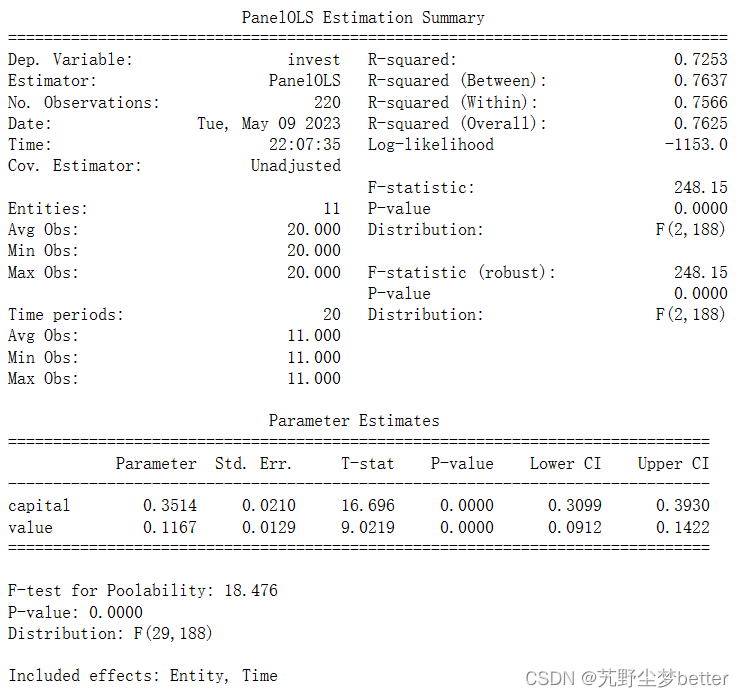
还有另一种使用直接使用PanelOLS方法的形式：

from linearmodels.panel import PanelOLS
from statsmodels.datasets import grunfeld
import statsmodels.api as sm
data = grunfeld.load_pandas().data
data = data.set_index(["firm","year"])
exog = sm.add_constant(data[['value','capital']])
grunfeld_fet = PanelOLS(data['invest'], exog, entity_effects=True, time_effects=True)
grunfeld_fet = grunfeld_fe.fit()
print(grunfeld_fet)

 如果想单独获取结果中的某一信息，如R方，回归系数，显著性，可以使用dir()函数来查看结果类中的属性，这里给出常用的几个：params（回归系数）、std_errors（回归系数标准误）、tstats（T统计量值）、pvalues（P值）、rsquared（R方）。

使用到的两个函数的定义的文档链接如下：

linearmodels.panel.model.PanelOLS - linearmodels 4.31 (bashtage.github.io)

linearmodels.panel.model.PanelOLS.from_formula - linearmodels 4.31 (bashtage.github.io)