一、什么是带头双向循环链表

在【数据结构】单链表中提到，链表为数据结构中的一种存储结构，链表属于线性存储结构，同时链表共有八种，此次所讲的链表为双向带头循环链表，属于链表中结构最复杂的结构；

带头双向循环链表是链表中带头（哨兵位）、双向、循环三种属性的结合体；
带头即带哨兵位，哨兵位只负责存储第一个具有有效数据的节点，本身不存放数据，该处因为为双向循环链表，代表也可访问该链表的尾节点；
双向即表示，每个节点不仅能访问该节点的后一个节点，同时也可访问本节点的前一个节点；
循环即表示，第一个节点的prev指向尾节点；

• 带头双向循环链表虽然在结构中是所有链表中最为复杂的，但是相比较于单链表的优势在于不需要多次对链表为空进行判断，避免了边界问题；
• 同时如单链表所言，单链表在进行每次尾删或者尾插时，都需要遍历到尾节点且保存尾节点的前一个节点，而对于双向链表而言，只需要访问头节点的prev即可；
• 总而言之，双向带头循环链表而言，虽然在结构上要比单链表复杂的多，但是在操作上确是比单链表而言简单；

二、带头双向循环链表的实现

（一）链表中结构体的声明

因为该链表属于双向循环链表，故需要使用两个指针，一个指针next来存放该节点的下一个节点，并使用prev指针来存放该节点的上一个节点；
同时，为了避免使用者在使用时需要修改所存储的数据，可以使用typedef对需要存储的数据类型进行重命名，方便后期对存储类型的修改；

#include<stdio.h>

#include<string.h>

#include<stdlib.h>

#include<assert.h>

typedef int DataType;

typedef struct ListNode {
	struct ListNode* next;
	struct ListNode* prev;
	DataType val;
}LTNode;

（二）头节点的创建（链表的初始化）

该链表为带头双向循环练表，因为存在哨兵位，所以在插入数据之前应给链表安排一个哨兵位，并对哨兵位进行初始化；

LTNode* ListCreate()//创建头节点(哨兵位)
{
	LTNode* newnode = BuyNode();
	newnode->next = newnode;
	newnode->prev = newnode;
	return newnode;
}

在对哨兵位进行初始化时同时也要注意该链表的结构为双向循环链表，在只有哨兵位的情况下，哨兵位的next与prev都指向自己；

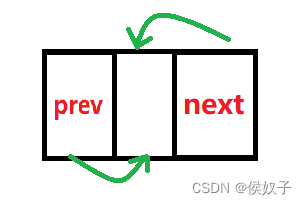
（三）新节点的创建

新节点的创建也与单链表的相同，唯一不同的就是新创建的节点需要注意双向循环的格式；

LTNode* BuyNode()
{
	LTNode* newnode = (LTNode*)malloc(sizeof(LTNode));
	if (newnode == NULL) {
		perror("BuyNode::malloc");
		return NULL;
	}
	return newnode;
}

（四）链表的尾插

若是在单链表中，尾插需要遍历整个链表找到尾节点，而在该链表中，因为链表头节点（哨兵位）所指向的prev即为尾节点；
故在该链表进行尾插时，只需访问哨兵位的prev所指向的节点；

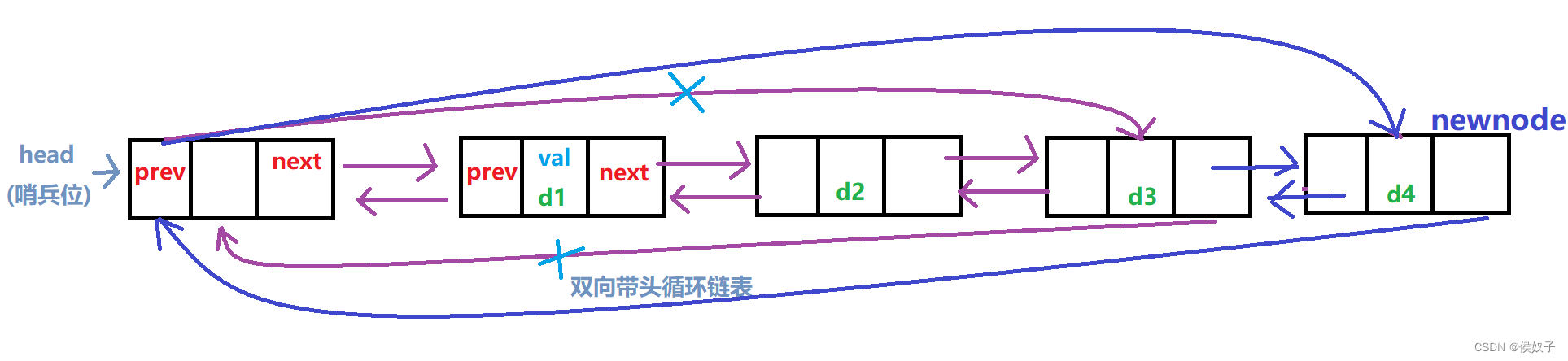
void ListPushBack(LTNode* phead, DataType x)
{
	assert(phead);

	LTNode* tail = phead->prev;
	LTNode* newnode = BuyNode();
	newnode->val = x;
	tail->next = newnode;
	newnode->prev = tail;
	newnode->next = phead;
	phead->prev = newnode;
}

（五）链表的尾删

在双链表中，链表的尾删只需释放头节点head内prev所指向的节点（尾节点）即可；

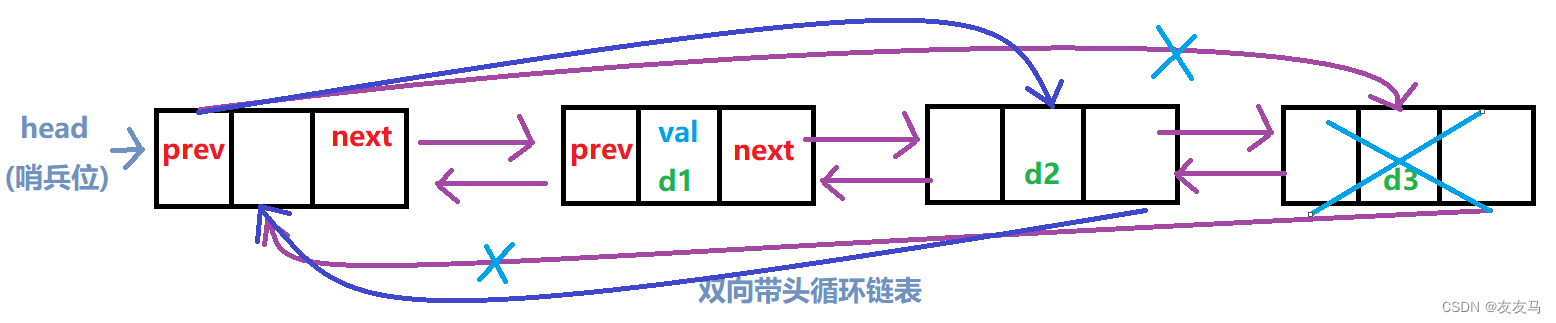
void ListProBack(LTNode* phead)//尾删
{
	assert(phead);
	LTNode* cur = phead->prev->prev;
	free(cur->next);
	cur->next = phead;
	phead->prev = cur;
}

（六）链表的头插

因为该链表存在哨兵位，故在进行头插时需要插入至头节点（哨兵位）之后；

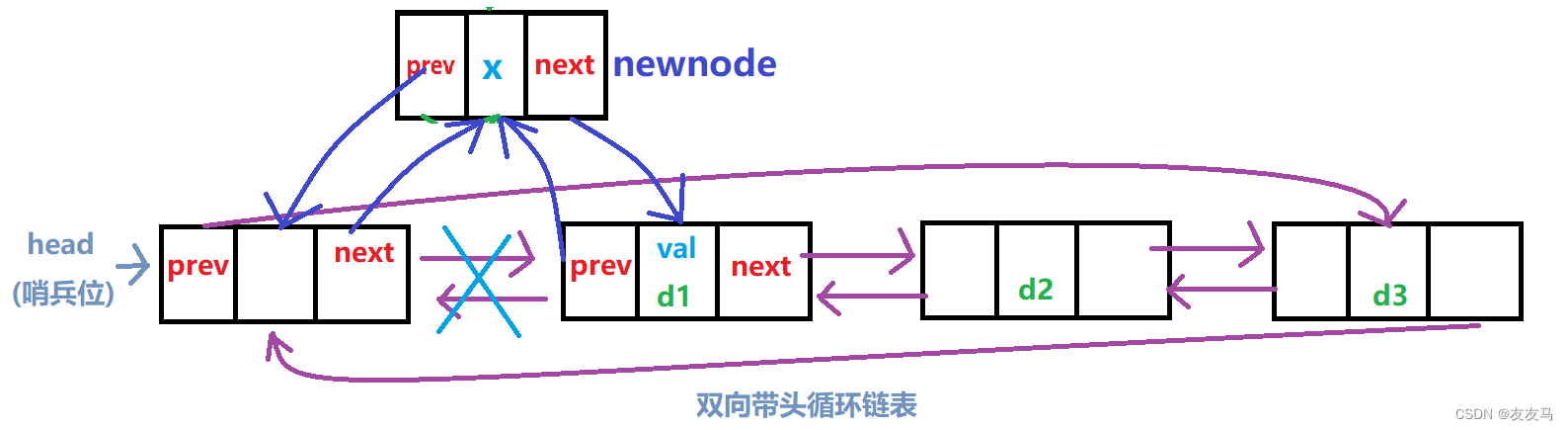
void ListPushFront(LTNode* phead, DataType x)//头插
{
	assert(phead);
	LTNode* newnode = BuyNode();
	newnode->val = x;
	LTNode* tail = phead->next;
	phead->next = newnode;
	newnode->prev = phead;
	newnode->next = tail;
	tail->prev = newnode;
}

（七）链表的头删

同样的带头双向循环链表在进行头删时只需要删除头节点（哨兵位）后的节点即可；

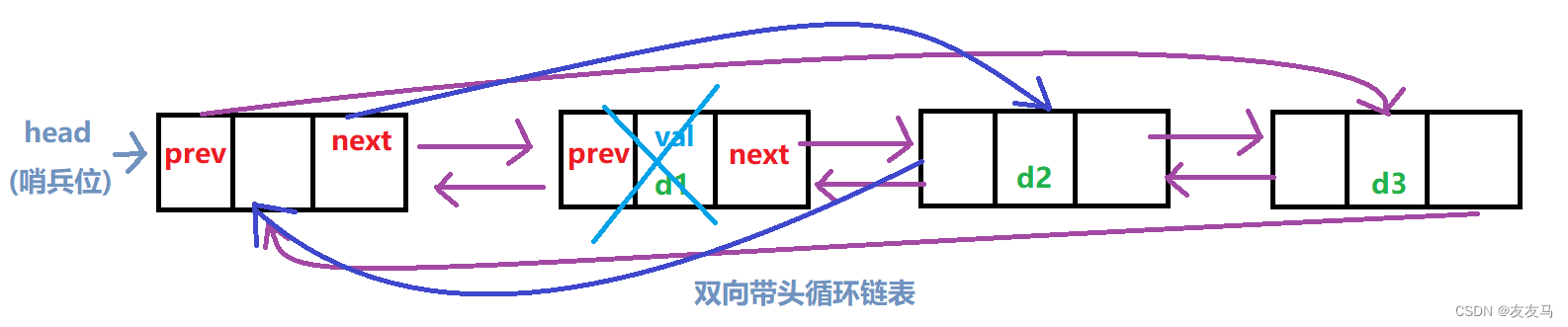
void ListProFront(LTNode* phead)//头删
{
	assert(phead);
	LTNode* tail = phead->next->next;
	free(phead->next);
	phead->next = tail;
	tail->prev = phead;
}

（八）链表的查找

双链表的查找，利用while循环对链表进行遍历，循环条件为当指针指向不为哨兵位；
若为哨兵位，则代表链表已经遍历了一次，若是找到对应val的值，则返回节点的地址，否则返回空指针；

LTNode* ListFind(LTNode* phead, DataType x)//查
{
	LTNode* tail = phead->next;
	while (tail->next != phead) {
		if (tail->val == x) {
			return tail;
		}
		tail = tail->next;
	}
	return NULL;
}

（九）链表节点的修改

参数给定节点的地址，通过地址访问该节点所对应的val并对其进行修改；

void ListModify(LTNode* pos, DataType x) //改
{
	assert(pos);
	pos->val = x;
}

（十）链表的中间插入（pos前）

相比较单链表来说，双向链表可以访问所给pos节点的前一个节点，而单链表若是需要进行在pos节点前进行插入则各项消耗都会增大；
参数给定一个pos指针，指针指向为需要插入的节点位置，将新的数据（节点）插入pos所指向节点的prev所指向的位置；

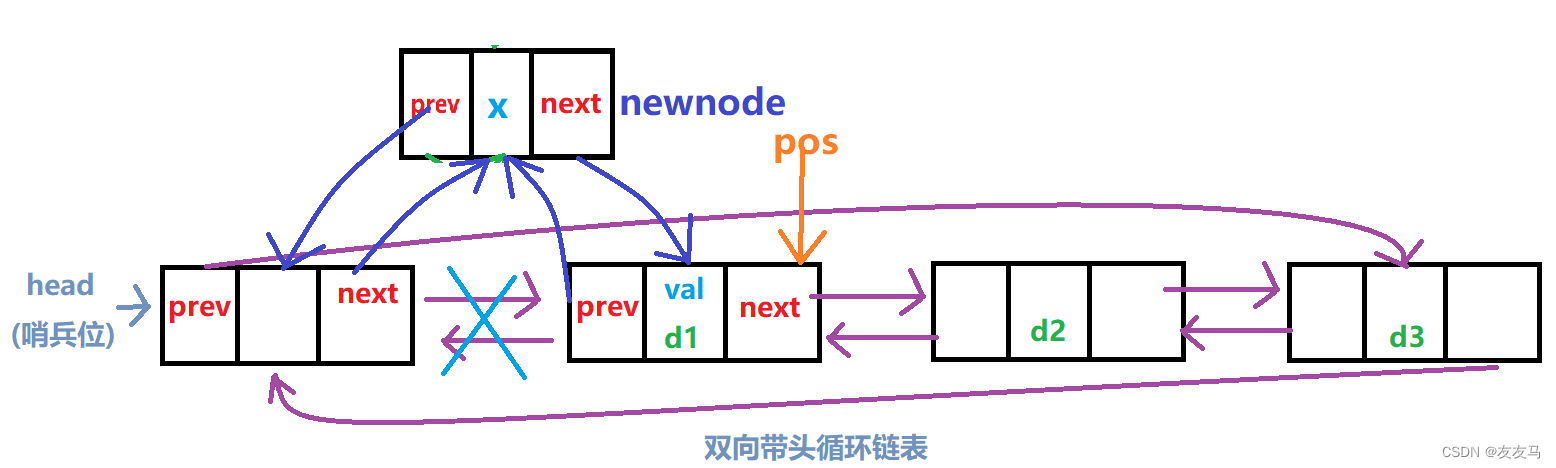
void ListInsert(LTNode* pos, DataType x) //中间插入(pos前)
{
	assert(pos);
	LTNode* tail = pos->prev;
	LTNode* newnode = BuyNode();
	newnode->val = x;
	pos->prev = newnode;
	newnode->next = pos;
	tail->next = newnode;
	newnode->prev = tail;
}

（十一）链表的中间删除

链表的中间删除则不需要再进行pos之后或者pos之前，双向链表既可以访问pos节点的next，又可访问pos节点的prev；
即在进行中间删除时，可以直接将pos节点进行删除；

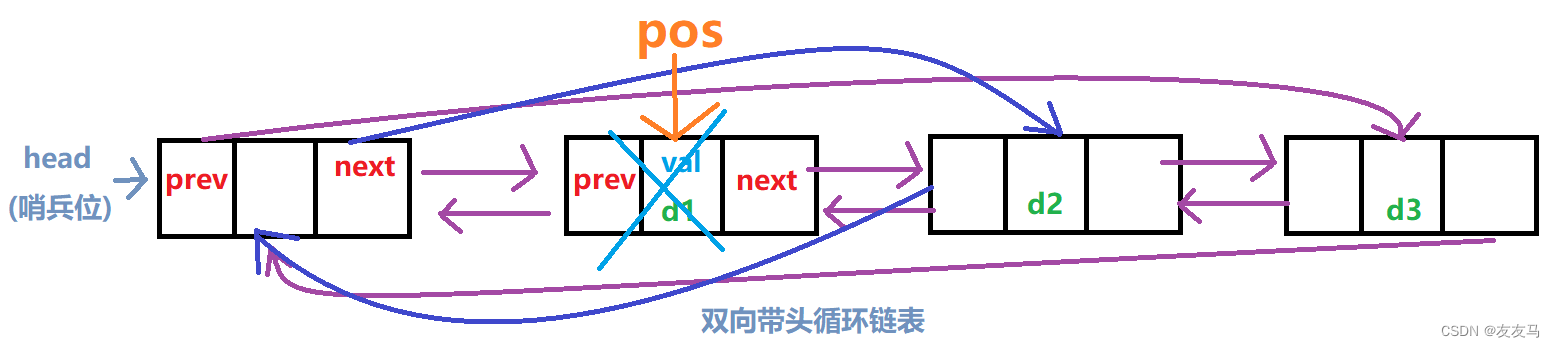
void ListErase(LTNode* pos)
{
	LTNode* tail = pos->prev;
	LTNode* cur = pos->next;
	tail->next = cur;
	cur->prev = tail;
	free(pos);
	pos = NULL;
}

（十二）链表的销毁

当使用完空间并不需要再使用时，应及时将空间进行释放，避免出现内存泄漏等问题，在顺序表中，可直接将malloc后的空间进行释放，因为在物理因素上，顺序表为一块连续不断的空间；
而链表则只在逻辑上具有连续不断的属性，在物理上本质是一块一块不同位置的空间；
双链表的销毁也与单链表的销毁逻辑相同；

void ListDestory(LTNode** pphead)//销毁
{
	LTNode* tail = (*pphead)->next;
	LTNode* cur = NULL;
	while (tail != *pphead) {
		cur = tail->next;
		free(tail);
		tail = cur;
	}
	free(*pphead);
	*pphead = NULL;
}

总结

• 带头双向循环链表在链表为空的情况下（只有头节点），头节点的next与prev指针都指向自己；
• 在写双链表的各个接口时应注意应尽量使用断言判断形参所接收的指针是否为有效指针；
• 使用完内存后应及时将内存还给操作系统（释放）；
• 带头双向循环链表与不带头单向不循环链表为链表中的两个极端，一种为八种链表中结构最复杂的链表；一种为八种链表中结构最简单的链表；但是反而再逻辑中，由于结构的特性，带头双向循环链表的逻辑是几种链表中逻辑最简单的；