您现在的位置是：首页 >学无止境 >【LeetCode】环形链表II+结论证明网站首页学无止境

题目链接：环形链表II

题目：给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。不允许修改 链表。

示例1:

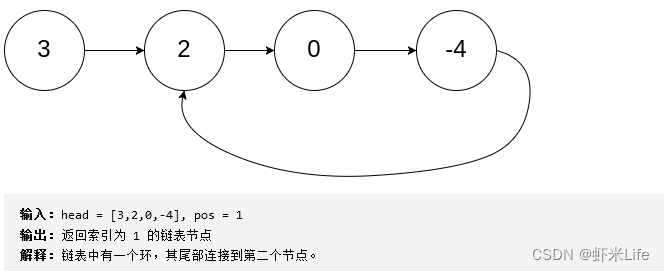
示例2:

•  解题过程 

1. 判断链表是否环
2. 如有环，找到入环口的节点.

判断是否有环我已经在这一节讲过了【LeetCode】环形链表+结论证明，大家可以先去看看，这一节主要讲解如何找到入环口，与推导过程。

• 找到入环口思路

如已知道链表已经有环，那么接下来要找这个环的入口了，我们定义一个从头结点出发的指针，从链表相遇节点也同时出发一个指针，这两个指针每次移动一个节点， 那么当这两个指针相遇的时候就是环形入口的节点。

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode* fast = head;
    struct ListNode* show = head;
    while(fast&&fast->next)
    {
         fast = fast->next->next;
         show = show->next; 
        if(fast == show)
        { 
            //那为什么两个指针会在入环点相遇呢？
            struct ListNode* index1  = fast;
            struct ListNode* index2  = head;
            while(index1 != index2)
            {
                index1 = index1->next;
                index2 = index2->next;  
            }
            return index1;// 返回环的入口
        }
    }
    return NULL;
}

• 不少人在刚开始做这题时都会有这样的疑惑，为什么两个指针会在入环点相遇呢？
• 接下来我们就推导证明一下.

 有的人是这样推导的：

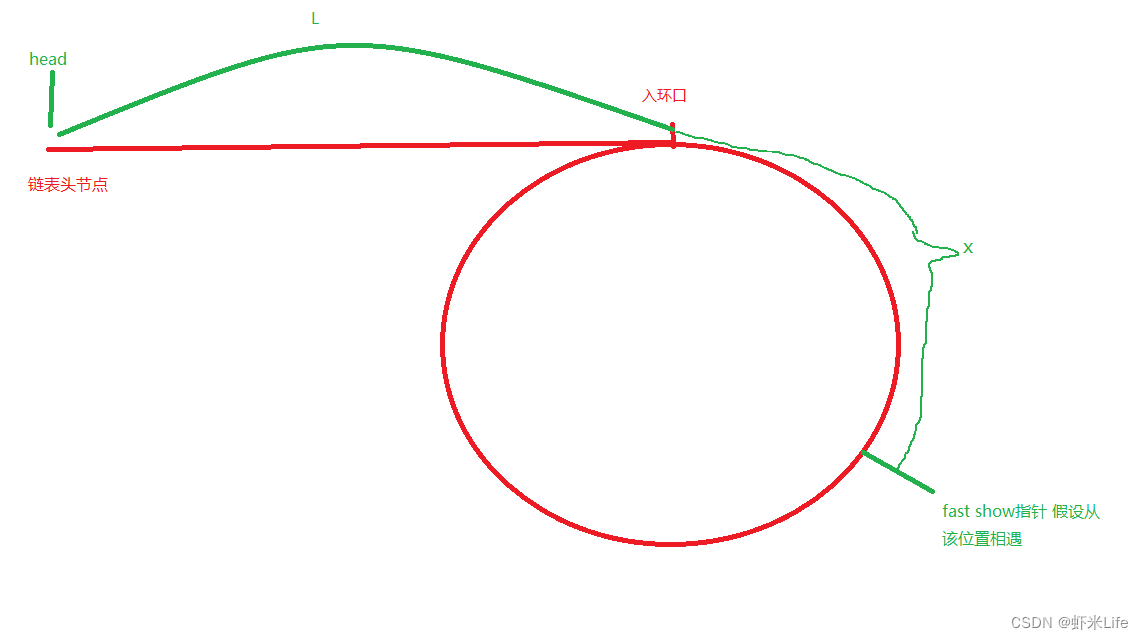
 fast走的路程是slow的两倍

假设:

链表头节点--入环口节点的距离为-> L.

入环口节点--相遇节点距离为-> X

环的长度为->C

slow指针走的路程是: L+X  分析:(有没有可能slow进环转了几圈才追上？ 答案是：不可能，肯定是在一圈之内，fast指针必然会追上slow指针，因为他们之间距离每次缩小1，不会错过，slow走一圈，fast都走了两圈了，肯定追的上.)

fast指针走的路程是：L+X+C

推导：

2*(L+X) = L+C+X   (慢指针走的路程两倍 等于 快指针的路程)

L + X = C  （两边同时约定一个L+X）

L = C - X    (环的距离 - 节点相遇距离 = 入环口)

---

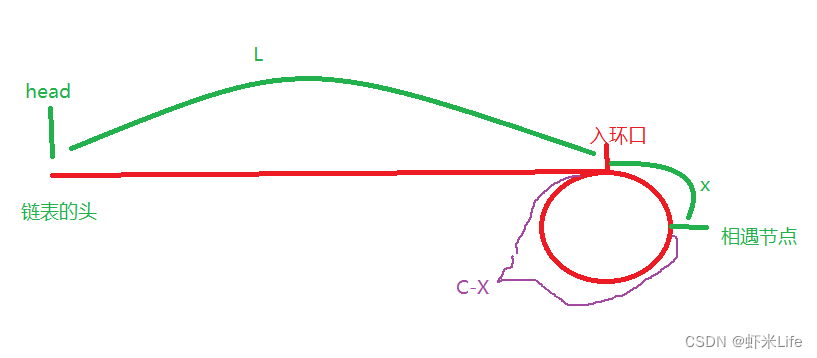
该推论是错误的！！如果下面环长这样呢？

 所以上面的推论只是在个别情况是正确的，那该如何推导呢？

假设：

链表头节点--入环口节点的距离为-> L.

环的长度为->C

入环口节点--相遇节点距离为-> X

 fast 走的路程是： L+N*C + X

( 假设N是slow进环前，fast在环里面转的圈数 ）

 推导：

 2(L+X) = L+N*C + X

 (两边同时约掉L+X)

 L+X = N*C

 L = N*C-X 

所以入环点是 fast在环里面转的圈数-相遇节点距离

这也证明了从头结点出发一个指针，从相遇节点同时也出发一个指针，这两个指针每次移动一个节点， 当两指针相遇时就是 环形入口的节点。